Clever Geek Handbook

AK-15量子密钥分发协议

希望了解量子密码协议之一的所有人都向他们致以问候，因为量子计算机在不久的将来可能出现会危害许多现有的密码学方法。

目前，已经提出了协议，您可以在Habré上找到对协议的详细分析，但是我可以向您推荐一篇概述不错的文章：单击此处。

值得注意的是，AK-15的显着特征是合法用户之间存在身份验证。

介绍

该协议由Khaled Elleyti和Abdulbast Abushgra在2015年提出，定义了我们长期的朋友Alice和Bob的互动。他们的沟通将由几个相互联系的阶段组成，并且在某些时候，由于使用了几种不同的沟通渠道，因此要求读者并行化。

一个小型的教育计划：

纠缠态的EPR通道

它基于爱因斯坦-波多尔斯基-罗森悖论。以下是一些有用的链接：

第一阶段

首先，爱丽丝必须将纯文本传递给鲍勃。它必须首先将其转换为位表示形式，然后转换为量子位（qubits）：

纯文本->位表示-> A，其中A是希尔伯特二维状态空间中的向量

A = \开始{cases} | f> =（\ alpha | 0> + \ beta | 1>），＆0 \\ | f> =（\ alpha | 0>-\ beta | 1>），＆1 \结束{cases}

在对纯文本执行了转换之后，由Alice将所得的量子位输入到矩阵（DM）的下三角中（如下图所示），并将相同的量子位输入到上三角中，但以随机方式进行。这些随机元素将在合法订户之间达成协议的阶段用作错误状态（可以在原始文章中进行研究）。此外，需要每条线的奇偶性，主对角线被填充。这种填充表格的方式可提供额外的保护，使其免受光子数除以PNS的攻击

爱丽丝填写的DM矩阵（绿色-原始行数，黄色-发送消息中的行数）

, . ( ),  Ikubit,    , (|×> |+>) . 

- , .

-

4- -

| \ Phi _ +> = \ frac {1} {\ sqrt2}（| 00> _ {AB} + | 11> _ {AB}）| \ Phi _-> = \ frac {1} {\ sqrt2}（| 00> _ {AB}-| 11> _ {AB}）| \ psi _ +> = \ frac {1} {\ sqrt2}（| 01> _ {AB} + | 10> _ {AB}）| \ psi _-> = \ frac {1} {\ sqrt2}（| 01> _ {AB}-| 10> _ {AB}）

Iepr :

字符串伊普
Iepr

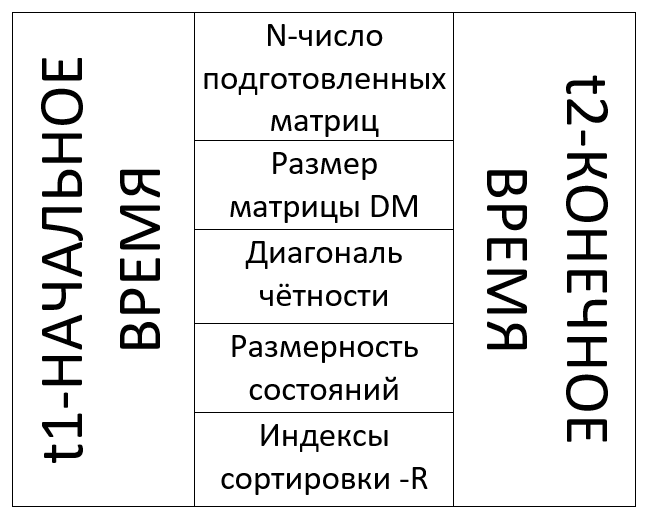
(t1,t2)- , ,  Iepr. N - ( ). DM, . p, , .S - , , . R - , .

:

-

, , - Iepr

  • ,

  • .

| \ Phi_ {ab}> \ otimes | \ varphi_c> = \ frac {1} {\ sqrt2}（| 0> _A | 0> _B + | 1> _A | 1> _B）\ otimes（\ alpha | 0> _C + \ beta | 1> _C）= \ frac {1} {\ sqrt2}（\ alpha | 000> + \ beta | 010> + \ alpha | 101> + \ beta | 111>）_ {ACB}

  • , :

| \ Phi _ {ABC}>：| \ Phi _ {AC}>，| \ phi _ {B}>

  • AC- , B- .

| \ psi_ {AC}> \ otimes（\ alpha | 0> + \ beta | 1>）_ B

,

  • , , (00,01,10 11) ( ),

( Iepr),   , . n- (SSK) n- ,  XOR. .

Iepr( ), Ikubit (|×> |+>) 4- ( ). ( ) . , Ikubit . QBERT( ), Iepr.

: Man-In-Middle(MIMA)  The Intercept-Resend Attacks. .

:

关于

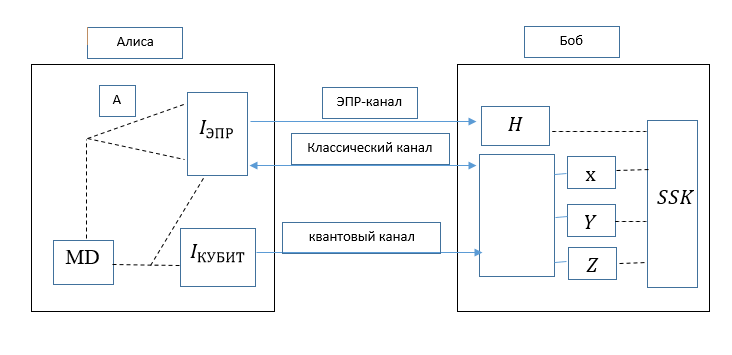
爱丽丝和鲍伯首先通过纠缠交换启动EPR通信。如果成功，则双方开始交换量子位以创建密钥。收到I kubit行后 ，Bob构建矩阵，并使用具有R索引的行来恢复正确的DM。并且它首先通过将奇偶校验字符串插入矩阵来进行调查，然后对每一行进行计数以查看其是否为偶校验。如果有奇数行，则必须检查是否有错误。如果一切成功，则生成n位量子密钥（SSK）。

作者的文章



More articles:


All Articles