介绍
最著名的加密问题是秘密消息的传输。对于此任务,最常用的是带有私钥的密码系统:Alice(发送者)使用密钥对信息加密,而Bob(接收者)使用它对消息解密。不幸的是,私钥密码系统在实际实施中有严重的困难。主要问题是如何分配密钥?在许多方面,密钥分发与私人通信的基本任务一样耗时。恶意第三方可以窃听密钥并轻松阅读消息。
为了避免这种情况,已经发明了许多方法,在本文中,我们将考虑量子,其中密钥的保密性由量子力学定律保证。第一个BB84量子密钥分发(QKD)方案是由物理学家Charles Bennett和Gilles Brassard在1984年开发的。它的主要思想是使用量子力学原理(不确定性原理),据此,观察整体上违反了被观察系统。因此,拦截器窃听了Alice和Bob的消息。然后,您可以轻松地计算出它并扔掉“坏”位,如果它们太多,请重新开始。
量子力学的基础
我们不会详细介绍,而只是简单地陈述主要声明。让我们从不确定性原理开始。它说某些物理量加在一起绝对不是精确测量的。让我们举一个例子来说明粒子的动量和坐标:如果将粒子放在可以精确测量坐标的设备中(例如,显示 ),然后在可以精确测量动量的设备中,第二个设备将给出一个随机数(让它为数字
,即
)。重要的一点:在它是具有坐标的粒子之前
,现在是具有动量的粒子
。如果将其放回测量坐标的设备中,它将给出一个随机数。
现在让我们继续进行极化(知道它是什么并不重要,我们将其视为表征粒子的物理量)。一个极化具有两个相互垂直的方向,并且知道什么极化,我们可以确定这些方向。假设我们有两个极化和
(符号表示极化的方向),每个极化分别具有两个状态。不确定性原理指出,没有设备可以区分所有4种状态。只有两个单独的设备,一个区分状态
,另一个
。BB84协议就是基于这一事实。
BB84协议
让我们写出我们的字典:
1)(下标表示量子态的基础)
2)
3)
4)
爱丽丝-转移;鲍勃-接受;前夕-拦截

1 .
|
|
(0 1). 0 1 | , , . , , , . |
. ( ). , , , . , "" ( ). - - . , . . BB84 11% [10], . .
. : . , , , (, , ). , , "" . : . (, , ). , , . , .
, :
1) , .
2) , .
BB84, , - -. . A B, C. : . A , B , C . , B , , . , A B. . ( ) .
|
|
, , . , . | , . |
, , 0 1.
. BB84 . BB84 , . , .
.
1
1)
2)
3) ,
, , .
1 . , . , , .
2 . . .
3 . - , . , . , , .
. , , , , . . a) (, , ); ) ; ) ) . "" , .
BB84 [7], . . [8]
H , QBER .
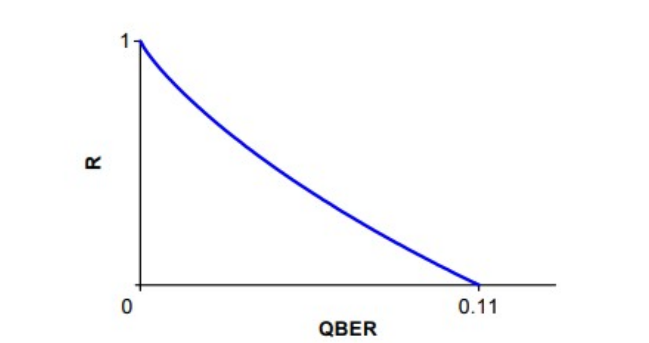
, . . , , . (, , ). , . PNS (photon number splitting)[2]. : , , . , , . , , [1].
2003 , BB84. , SARG04, BB84, . - -, [4]. , [4]. , , -. , . - . , PNS . Lo05[5]. - . ( - GLLP[3]) , . , ( .3).

SARG04[1]. : . ( !!!). , BB84, . , , :
.
( , ).
, , ( ). .
(
)
, ( ).
( 1/4), ,
(
,
,
). PNS : , 1 2 , 3 . [1].
, . SARG04 LPA(large pulse attack). , ( ). . , [6].
, . , . . , id Quantique [9], .4
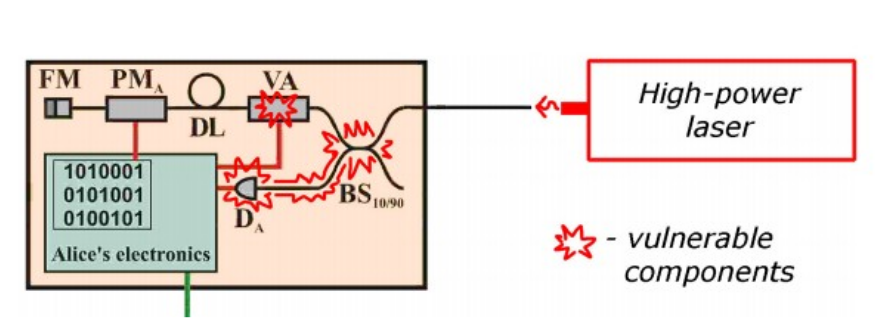
DA, , , . , . , , . ( ). : 1) ; 2) , ; 3) BS (, ); , , , , .
, , . . . . .
, ? : , , , . 1984 - , ? , , (RSA). , 1994 . , . , , .
:
1) A. Acin, N. Gisin, and V. Scarani, “Coherent-pulse implementations of quantum cryptography protocols resistant to photon-number-splitting attacks”
2) C. Bennett, F. Bessette, G. Brassard, L. Salvail, and J. Smolin, “Experimental quantum cryptography”(1992)
3) D. Gottesman, H.-K. Lo, N. L ̈utkenhaus, and J. Preskill, Quant. Inf. Comp. 4, 325 (2004)
4) W.-Y. Hwang, “Quantum key distribution with high loss: toward global secure communication”
5) Lo H., Ma X., Chen K. , “Decoy state quantum key distribution”, (2005)
6) Vadim Makarov, “Quantum cryptography and quantum cryptanalysis ”, (2006)
7) D. Mayers, “Quantum key distribution and string oblivious transfer in noisy channels” (1996); D. Mayers, “Unconditional security in quantum cryptography” (2001).
8)P. Shor和J. Preskill,“ BB84量子密钥分发协议的安全性的简单证明”(2000年)。
9)D. Stucki,N。Gisin,O。Guinnard,G。Ribordy和H. Zbinden,“使用即插即用系统在67公里范围内分配量子密钥”
10)谭晓庆,“量子密码学简介”,(2013年)