🎗️ 🧚🏼 👩🏼‍💼 如何在黑客马拉松的帮助下与数学家和ML专家面对面，然后谁将获胜 ♟️ 🎅🏼 💆

介绍

本文是关于我们如何与俄罗斯石油公司的子公司Samaraneftekhimproekt和喀山联邦大学在2020年9月举行的“三座城市”黑客马拉松比赛中，我们邀请学生解决反射地平线的地震相关性这一经典问题。这些是全球地震专业人士每天面临的挑战。对于参与者，他们决定将问题表示为“寻找最佳路径的问题”，以免用可怕的话语吓students学生。在本文中，我们将向您详细介绍该问题，并分析参与者的有趣解决方案。对于应用数学建模以及机器学习和数据分析人员而言，这将是令人兴奋的。

组织部分

我们在vc.ru上的文章-Oil and Hackathon中描述了在三个城市组织在线黑客马拉松的有趣细节。马拉松不仅仅是跑步。

我们只会提到，对于在线格式，我们选择了Discord服务，并且将保留指向黑客马拉松规则的链接（Boosters网站上的链接）。

问题的提法

在地震勘探中，存在``地震反射层''的概念-这是在动力学和传播区域方面的稳定反射波，它对应于某个地质边界。正确处理现场地震数据并识别（地震勘探专家说-“解释”）地震层位，就可以确定其发生深度，准确度为5-10米。确定深度后，再与地质学家一道，可以将这些视界与地质年代标度（Geochronological scale-Wikipedia）联系起来，并认识到它们较小的对应物。然后确定-疏水器可以位于哪个视野之间，该油田的结构模型的浮雕看起来是什么样的，等等。

地震立方体的垂直截面和公认的地震反射层位

在实践中，层位是在地震立方体的地震层上逐层区分的-既可以手动使用大量参考点的阵列（地震专家称“潜水”），也可以使用自动和半自动搜索程序...当然，对使用软件解释地震层的问题的高质量解决方案有很高的要求，并且可以大大减少地震勘探专家所花费的时间。

同时，研究信号源（具有局部斜率和多网格相关性的最小二乘视野，波形嵌入：无监督深度学习的自动视野选择））表明已开发的算法和解决方案基于少量的数学方法，因此我们决定尝试吸引尚未被科学研究遮盖的意识的学生，并以在复杂表面上找到最佳路径的问题的形式向他们提供此问题。

结果，该问题被表述为：在复杂的表面上构造运动路径，该复杂表面通过给定的点并满足特定功能中最小值的条件，这取决于该路径的长度及其角度（梯度）。

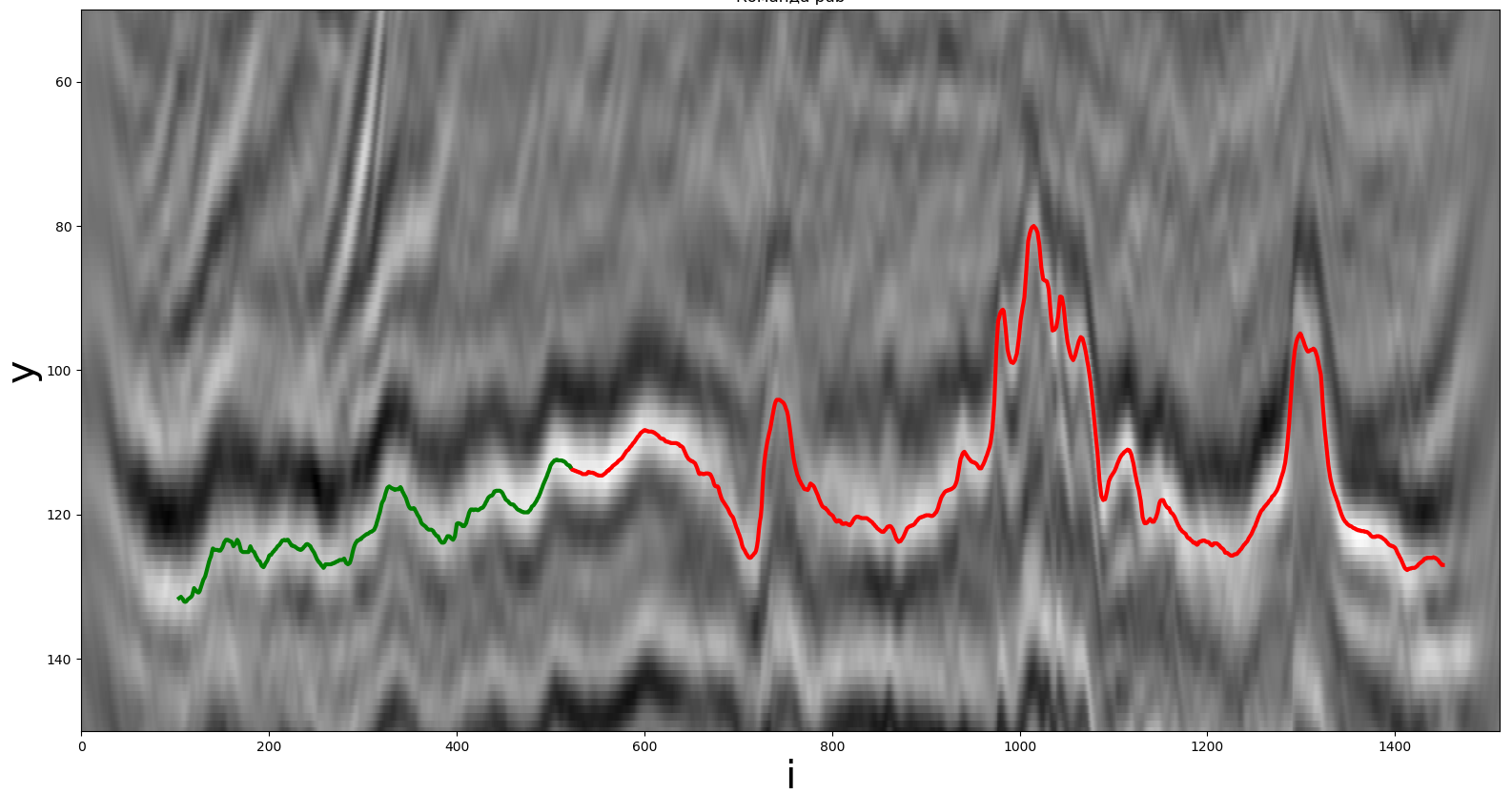
用于构建地平线的原始地震剖面的一部分的示例。绿线是事先已知的部分，红线是所需的部分。

比赛的参与者必须在12小时内找到解决方案，使他们能够沿着数据集隐藏部分上的最佳轨迹继续前进。进行了20次验证解决方案的尝试；赢得了最小度量值的参加者。

详细数据说明

, :

. , [x,y] z(x,y) .
(x,y) L1 L2. x, hor_1, …, hor_4.
L2 4 (1, 2, 3, 4), L1 – 3 (1, 3, 4). 2- L1 (40%). 60% .

, – 2 .

-, hor_2 L1. L2 L1. . , , .

在整个比赛中，排名是根据测试数据公开部分的指标值建立的。比赛结束后，将在私有部分重新计算指标值，并更新排名。这对于获得可持续的解决方案非常重要，即不仅要针对公共数据量身定制，而且还要能够在私有数据上显示可比的结果。事实证明，这并非徒劳，并且在最终质量评估之后，排名有所变化。

为了量化获得的结果，使用了以下指标：

F (\hat{y}, \hat{z}) = \sqrt{\sum_{i = 0}^{N} ({\hat{y}}_{i}^{p r e d} - {\hat{y}}_{i}^{e t a l o n}) + {(\hat{z} (i, y_{i}^{p r e d}) - \hat{z} (i, y_{i}^{e t a l o n}))}^{2}}

$F\left (\widehat{y},\widehat{z} \right ) = \sqrt{\sum_{i=0}^N\left(\widehat{y}_{i}^{pred} -\widehat{y}_{i}^{etalon} \right)+\left(\widehat{z}\left(i,y_i^{pred}\right) - \widehat{z}\left(i,y_i^{etalon} \right) \right)^2}$

其中：

N是所需范围的尺寸；

y_{i}^{p r e d}

${y}_{i}^{pred}$ -使用算法获得的地平线坐标，

i \in \bar{0, N}

$i\in\overline{0,N}$ ;

y_{i}^{e t a l o n}

${y}_{i}^{etalon}$ -参考地平线的坐标；

\hat{z} (i, y_{i})

$\widehat{z}\left(i,y_i\right)$ -坐标为i，yi的点的表面贴图的值;

{\hat{y}}_{i} = \frac{y_{i}}{h e i g h t}

$\widehat{y}_i = \frac{y_i}{{height}}$ ，其中height是表面图的y坐标的最大可能值；

\hat{z} (i, y_{i}) = \frac{z (i, y_{i})}{m a x (z)}

$\widehat{z}\left(i,y_i\right) = \frac{z\left(i,y_i \right)}{{max \left(z \right)}}$ 其中max（z）是曲面图的最大值。

Python中的指标实现

def score(true, submission, all_data):
   #true – pandas.Dataframe    ;
   #submission - pandas.Dataframe   , 
   #;
   #all_data - numpy.ndarray    
   all_data = all_data.astype('float64')
   #    
   max_z = abs(all_data).max()
   #   
   y_pred = submission.loc[idx.index.values].y.values.astype('int')
   #  
   y_true = true.y.astype(int)
   #     
   z_pred = all_data[true.index.values.astype(int), y_pred.astype(int)]
   #     
   z_true = all_data[true.index.values, y_true]
   #   
   y_err = ((y_pred - y_true)/3000)** 2
   z_err = ((z_pred - z_true)/max_z) ** 2
   #     
   total_err = np.sqrt(np.sum(y_err + z_err))
   return total_err

团队使用了什么方法

最初选择问题的方式是可以通过几种方式解决该问题：正向和逆向（分别使用经典的数学方法和机器学习方法）。

从机器学习的角度来看，可以通过两种方法解决该问题：

1）

使用已知的点对构造回归

x_{i}, y_{i}

$x_i,y_i$ ），您可以构建一个映射

f : ϕ (x_{i}) \mapsto y_{i}

$f:\phi \left(x_i \right)\mapsto y_i$ 通过最小化损失函数L

ϕ (x_{i})

$\phi \left(x_i \right)$ -第i点的指示性描述。

例如，

ϕ : x_{i} \mapsto x_{i}

$\phi : x_i \mapsto x_i$ 要么

ϕ : x_{i} \mapsto (x_{i}, x_{i}^{2}, x_{i} \cdot x)

$\phi : x_i \mapsto \left( x_i,x_i^2,x_i \cdot x \right)$

损失函数可以是问题陈述中的初始误差函数，也可以是更简单的函数，例如，构造路径和原始路径的标准偏差：

\frac{1}{N} \sum_{i = 0}^{N} {(y_{i} - {\hat{y}}_{i})}^{2}

$\frac{1}{N} \sum_{i=0}^N \left( y_i - \widehat{y}_i \right)^2$

许多流行的机器学习方法可用于构造映射f：从多项式回归开始，遍历随机森林和深层神经网络。

一些团队采用了这种方法

ϕ

$\phi$ 卷积或完全连接的神经网络，以及f-神经网络或高斯过程。

2）语义分割语义分割

的示例

原始问题可以作为计算机视觉问题来解决。点（x，y）被视为图像像素，其中整个图像是整个数据集，而像素（x，y）的“亮度”是z（x，y）值。要构建路径，您需要为每个像素分配一个类-0或1。该路径下方或包含该类的图像部分属于类0，其余部分属于类1。此类问题的日常解决方案是使用全卷积神经网络U-Net，一种输入，接收一块原始图像（补丁），并输出大小相同的数组，该数组由零和一组成，表示相应像素的类别。

除了深度学习技术外，您还可以使用经典的计算机视觉和图像处理技术（例如Flood Fill）进行图像分割。这是由一名参与者完成的，从而对图像进行预处理，以进一步应用算法来找到最短路径。

从经典数学方法的角度来看，提出的问题是经典优化问题，我们观察到尝试通过以下几种方法来解决该问题：

, ;

. y , y, .
, ;

$y_i$ .
, .

, .

首先，让我们分析参与者的决定。

机器学习方法：

解决方案之一是产生实际数字-路径值的自回归卷积神经网络

{\hat{y}}_{i}

$\widehat{y}_i$ 对于第i步。原始图像的32x32像素斑块被馈送到神经网络输入。作为功能

ϕ

$\phi$ 对于特征提取，使用了预训练的卷积神经网络ResNet34。通过该神经网络获得的特征表示与之前32个步骤中该路径的值相结合。为了预测其他32个步骤，将先前的神经网络预测用作先前的层位值。通过修改Adam的随机梯度下降来训练神经网络，在训练过程中优化器步骤呈指数下降。对于训练，平均绝对偏差被最小化（标准偏差的实验给出了较差的结果）。为了避免过度拟合，使用了Dropout，即对一部分神经元进行随机调零。训练神经网络花了大约10分钟，整个数据集进行了20次完整遍历，并执行了720个优化步骤。

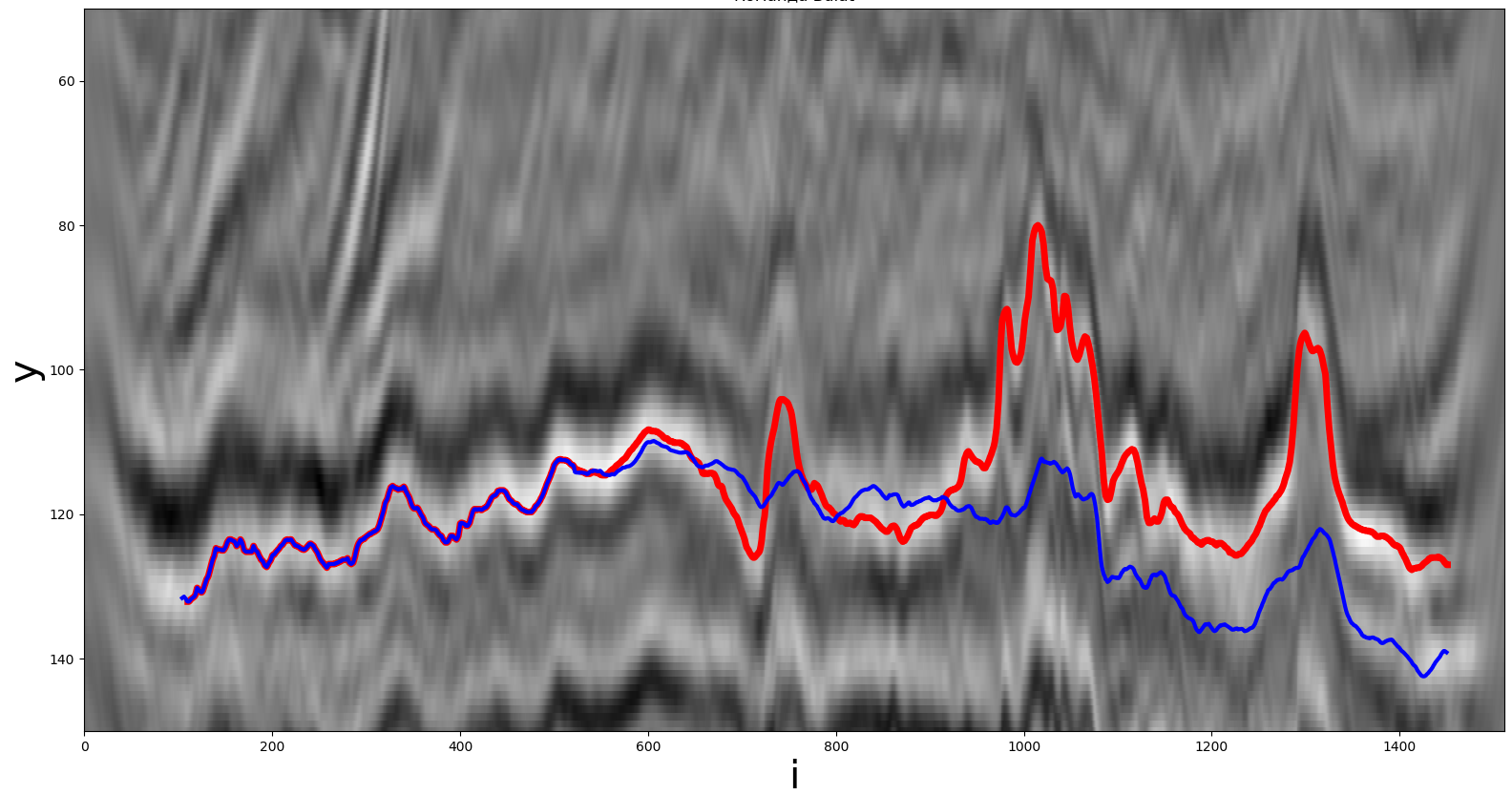
使用卷积神经网络获得的解决方案。红线是真实路径，蓝线是参与者收到的路径。

在AMD Threadripper 2950x CPU和Nvidia GTX 1080 Ti GPU上，神经网络预测大约需要1分钟。

公众席上的神经网络（度量）结果为5.71。还进行了用循环神经网络代替卷积神经网络的实验，但是结果却更糟。结果，经典的计算数学方法被用作最终解决方案。

除了完成的解决方案外，参赛者还分享了他们的想法，由于比赛时间紧且想法的计算复杂性，他们未能实现。他们中的一些人尝试应用神经网络，但是在花费了大部分时间之后，他们转向了更简单，更高效的算法，甚至转向了蛮力和规则，最终获得了最佳结果并获得了奖励。

同样，许多有趣的解决方案都是基于其他学科的知识得出的：例如，经典计算机视觉和图像处理，图论，时间序列分析。其中一个团队甚至从您可能听说过的强化学习中提出了这个问题，并提出了解决方案，但是不幸的是没有时间实施它。

经典数学方法：

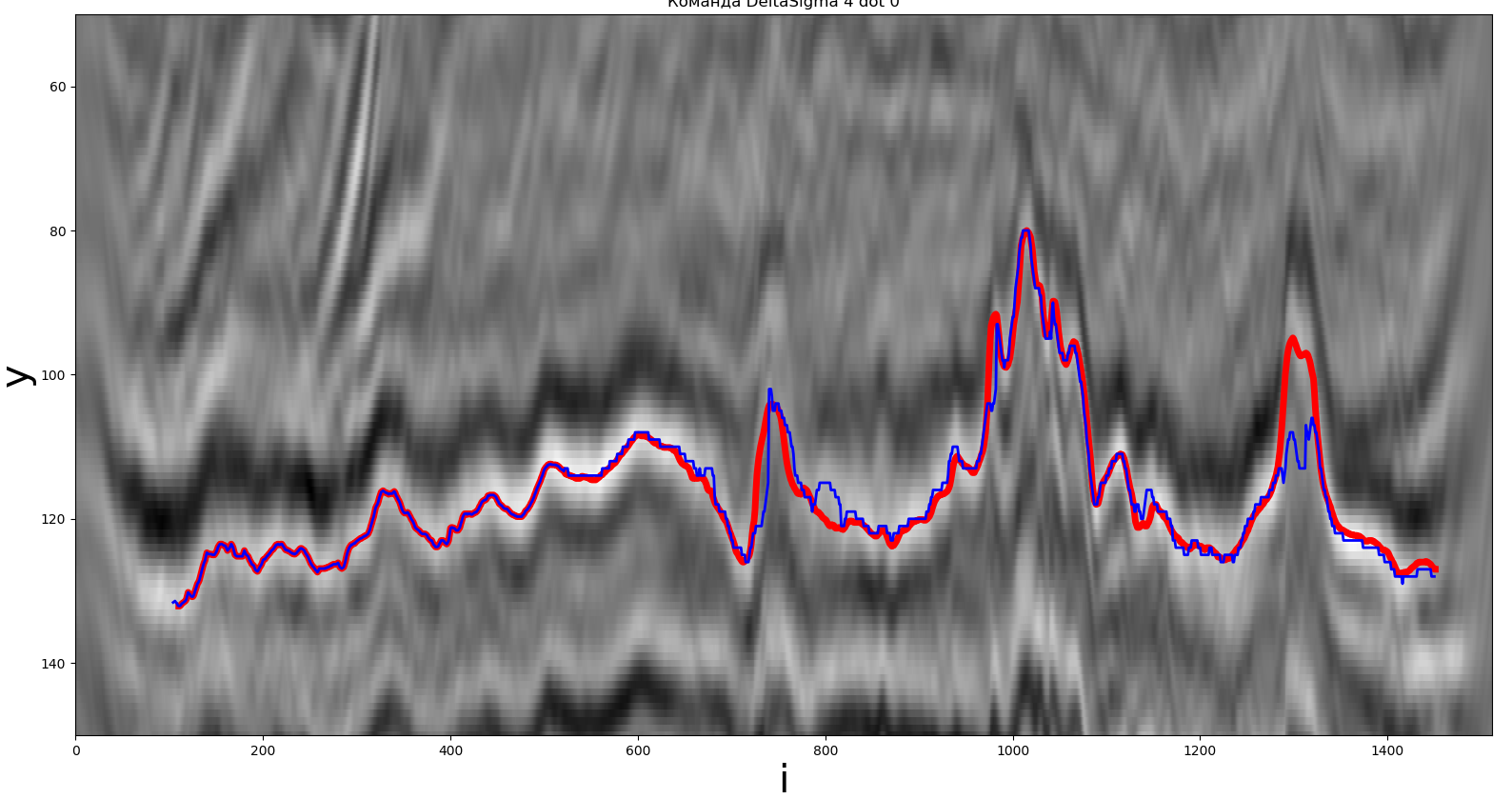
通过局部极值法获得的解决方案之一。红线是真实路径，蓝线是参与者收到的路径。

对于此方法，将局部最大值用作极值。参与者建立的路径标记为蓝色，所需的地平线标记为红色。下面提供了详细描述。

y_{i + 1} = m i n | j - y_{i} |, \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1} = min \left| j-y_i \right|, \forall i \in \overline{0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)> z(i,m-1) \cap z(i,m) > z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$ ，

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ，

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y}

$m_2=min(height - 1,y_i + size_y$ ，

其中：

h e i g h t

$height$ -表面图的y坐标的最大可能值；

s i z e_{y}

$size_y$ -搜索窗口的大小。

该方法在Python中实现。工作时间约为0.103秒，F（y，z） = 1.57，

s i z e_{y}

$size_y$ =100。

结论：该方法易于实施，运行时间不超过0.1秒。

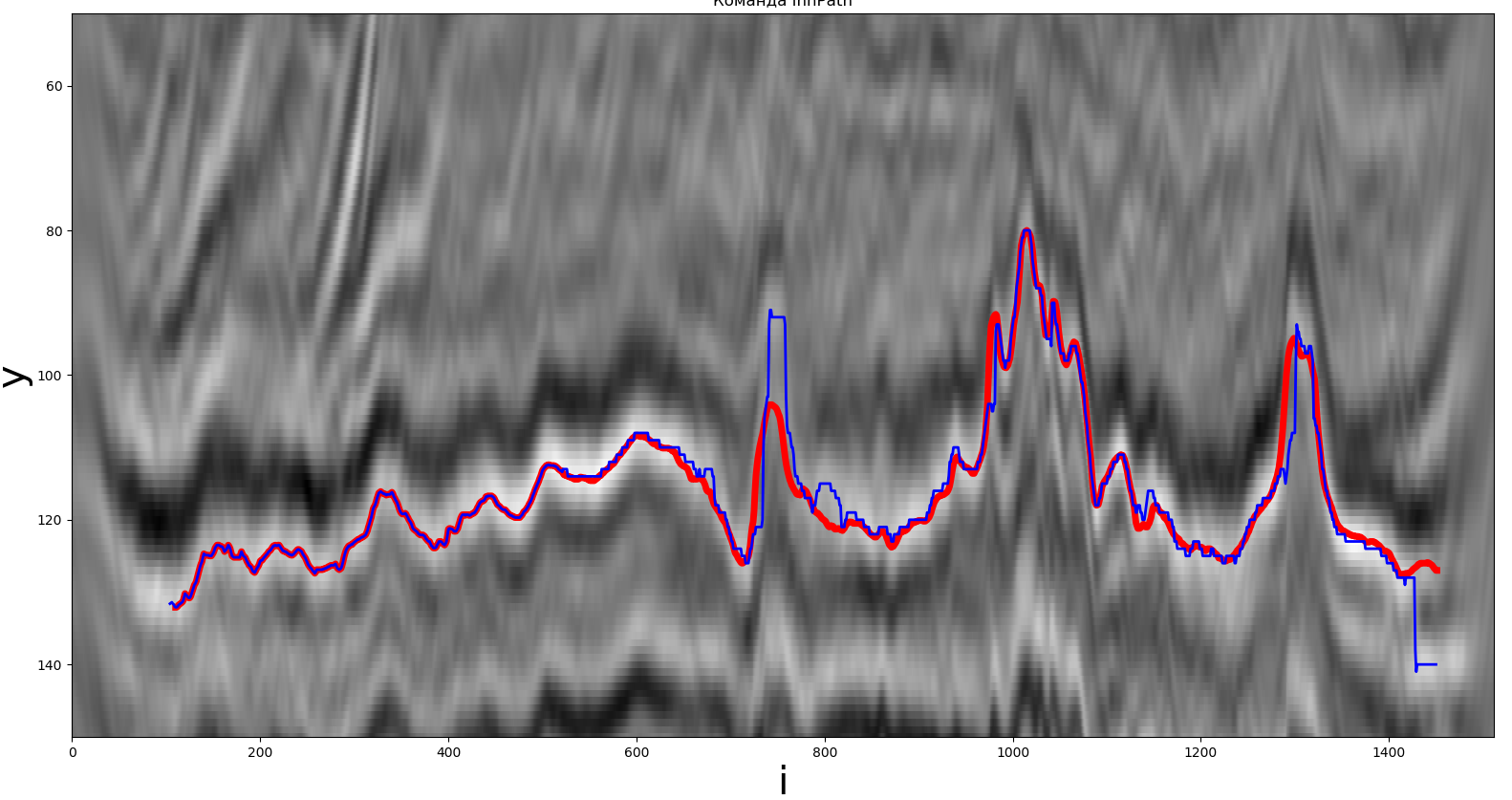
全球极值解决方案之一。红线是真实路径，蓝线是参与者收到的路径。

让我们继续下一组。与以前一样，在此方法中，最大值用作极端值。

y_{i} = a r g m a x (\frac{1}{s i z e_{x}} \sum_{j = 0}^{s i z e_{x} - 1} z (i + j, m))), \forall i \in \bar{0, N}, m \in \bar{m_{1}, m_{2}}

$y_i= {argmax}\left(\frac{1}{size_x} \sum_{{j=0}}^{{size_x-1}}z (i+j,m))\right), \forall i \in \overline {0,N}, m \in \overline{m_1,m_2}$ ，

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ，

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ，

其中：

height是曲面图的y坐标的最大可能值；

s i z e_{x}, s i z e_{y}

$size_x,size_y$ -搜索窗口的大小。

该方法在Python中实现。工作时间约为0.19秒，F（y，z）= 1.97，

s i z e_{x}

$size_x$ = 9

s i z e_{y}

$size_y$ =21。

结论：该方法易于实施，运行时间不超过0.2秒。

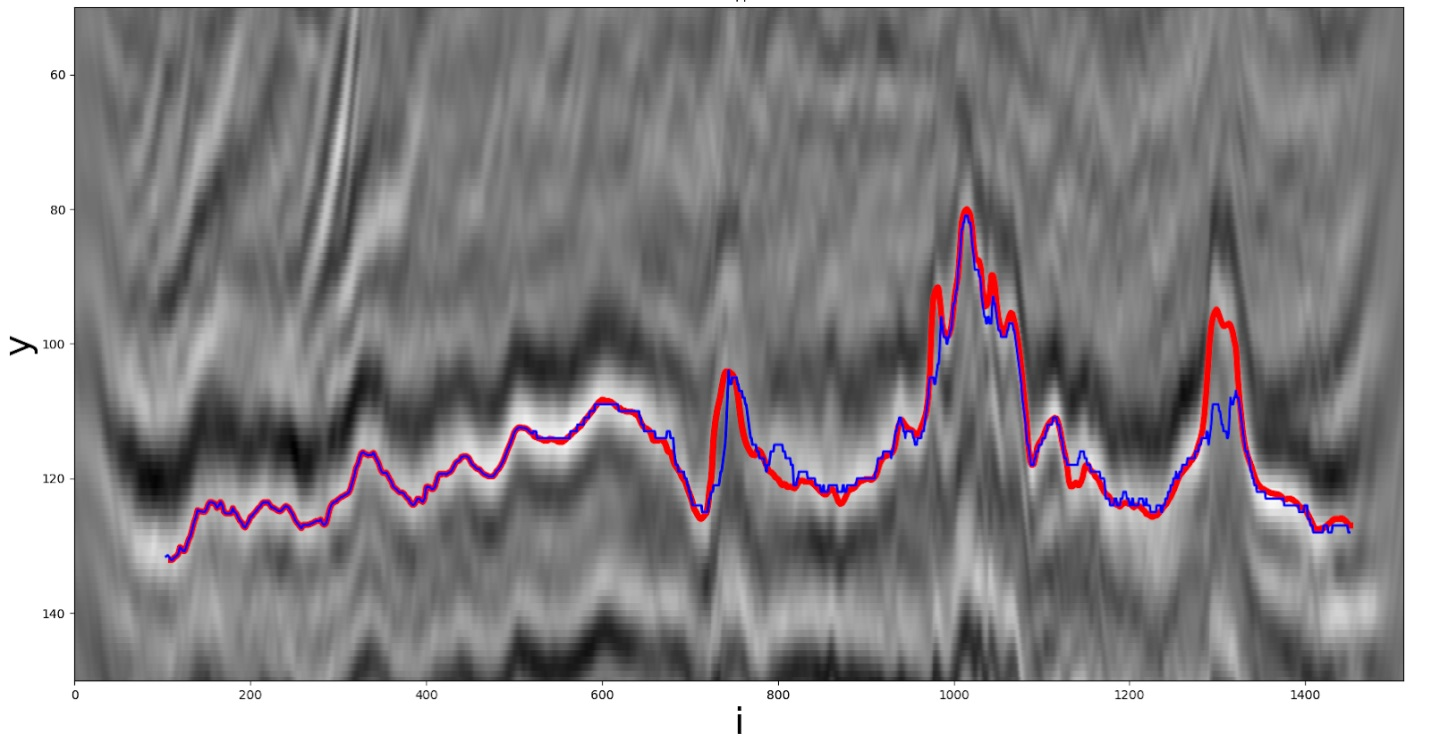
启发式解决方案之一。红线是真实路径，蓝线是参与者收到的路径。

让我们看看最后一组方法。如前所述，下一个坐标

y_{i} + 1

$y_i+1$ 在指定的搜索窗口内通过最少的功能进行搜索。

以下是团队建议的功能之一。从数学角度来看，它看起来像这样：

y_{i + 1} = m i n (\frac{(z (i, j) - z (i, y_{i}))^{2}}{m a x^{2} (z)} + α \frac{(j - y_{i})^{2}}{{h e i g h t}^{2}}), \forall i \in \bar{0, N - 1}, j \in Ω,

$y_{i+1}= {min}\left(\frac{(z(i,j)-z(i,y_i))^2}{max^2(z)} + \alpha \frac{(j-y_i)^2}{{height}^2}\right), \forall i \in \overline {0,N-1}, j \in \Omega,$

Ω = {m | z (i, m) > z (i, m - 1) \cap z (i, m) > z (i, m + 1), \forall m \in \bar{m_{1}, m_{2}}}

$\Omega = \left \{ m|z(i,m)>z(i,m-1)\cap z(i,m)>z(i,m+1), \forall m \in \overline {m_1,m_2} \right \}$

m_{1} = m a x (1, y_{i} - s i z e_{y})

$m_1 = max(1,y_i - size_y)$ ，

m_{2} = m i n (h e i g h t - 1, y_{i} + s i z e_{y})

$m_2=min(height - 1,y_i + size_y)$ ，

其中：

h e i g h t

$height$ -表面图的y坐标的最大可能值；

α

$\alpha$ -负责y误差对函数值的影响的系数；

s i z e_{y}

$size_y$ -搜索窗口的大小；

m a x (z)

$max(z)$ 是曲面图的最高值。

该方法是用Python实现的。工作时间约为0.12秒，F（y，z） = 1.58，

s i z e_{y}

$size_y$ = 50，

α

$\alpha$ = 15000.7。

结论：该方法的运行时间不超过0.15秒。

在给定的数据集上，所有三组方法均显示出相当相似的结果。通过在给定的搜索窗口内搜索表面值的局部极值的方法实现了最小度量值（1.57）。

最后部分

不幸的是，在黑客马拉松结束时，几乎所有创新者都~~转向了黑暗的一面，经过~~重新训练并变得保守，也就是说，他们开始使用经典算法发送解决方案……而保守派赢得了胜利。

我们希望汇集来自两个领域的贡献者：计算数学和机器学习。一些习惯于处理未知性质的非结构化数据，而另一些习惯于研究物理过程并在其基础上建立数学模型。为了增加想法和解决方案的多样性，我们简要介绍了如何获取数据。这是基于简单数值方法的解决方案获得最佳结果的原因之一。第二个原因是，对于学生黑客马拉松，我们准备的数据量不是非常“复杂”，因此，现代的耗时机器学习方法无法替代其他简单方法。

我们认为这是一个极好的课程，它将帮助参与者正确设置问题并选择解决问题的最佳方法。重要的是要记住，首先您应该尝试一个简单的解决方案，即所谓的基准，也许它可以使您在短时间内实现目标。

Hackathon的参与者提出了他们自己的算法，用于在大数据集中找到与自动地震运动学解释有关的最佳路径，目前正在将其作为地质和地震领域公司软件开发的一部分加以解决。算法中最具竞争力的实现将在这些软件系统的软件模块的开发和实现中找到其应用。

我们很高兴在11月28日在线举行的IT竞赛马拉松决赛中见到您。该计划包括：奖励比赛的优胜者，展示移动应用程序的第一版，以快速评估支撑剂质量。此外，在活动的框架内，还将组织有关“数据管理和DS项目”和“计算机视觉”主题的小组讨论。阿尔法数据科学负责人，CDO Megafon，华为负责人，CV X5负责人等代表将分享有趣的案例，不要错过所有的乐趣（IT竞赛马拉松2020-Rosneft）。

如何在黑客马拉松的帮助下与数学家和ML专家面对面，然后谁将获胜

介绍

组织部分

问题的提法

团队使用了什么方法

最后部分

More articles: