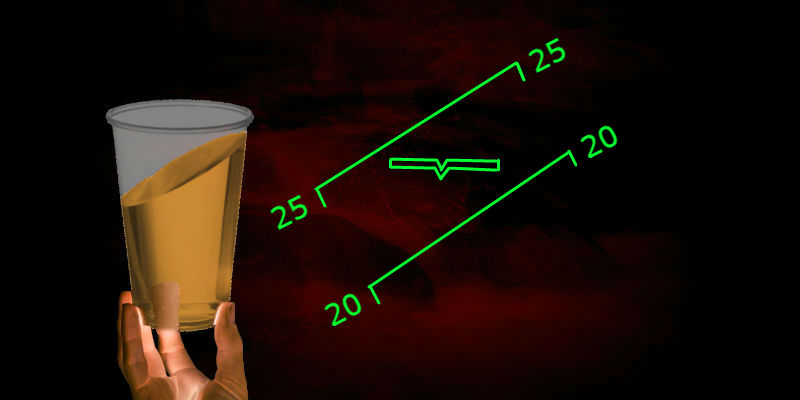
下面，我们将通过HTML5展示一种用于可视化受控对象的空间位置的不寻常想法之一的实现。该代码可用于模拟在三维空间中驾驶车辆的浏览器游戏。呈现信息的方式集中在Subterins或其他出色机器的模拟器上。

人工视界的目的和范围

这里所考虑的狭义的人造水平是物体相对于局部垂直方向的倾斜的可视化，用于控制其运动。倾斜度由两个欧拉角的值（roll和pitch）定义。水手们更喜欢同义词“ trim”而不是航空术语“ pitch”。

与人工视界（但不是很同义）相关的俄语术语：“人工视界”，“飞行指挥装置”。在英语中，使用了“姿态指示器”，“人工视界”或“陀螺视界”的表述。

已知的可视化技术

为了航空业的利益，进行了最多的关于在俯仰和横摇指示领域找到成功解决方案的工作。对此有一个简单的解释：飞行员必须快速阅读信息，任何对太空的感知错误都可能致命。

侧倾和俯仰指示领域中的大多数已知解决方案都是基于飞机轮廓和特殊背景的使用。一般特征：

背景通过一条代表地平线的线分为两个部分，分别象征天堂和大地。
飞机的轮廓是简化的“后视”，与背景形成鲜明对比。
侧倾角由指示器确定为符号水平线与连接轮廓的翼尖的线之间的角度（通常存在参考刻度以进行准确读取）；
根据控制点在轮廓中心的位置，沿垂直于条件水平线的刻度测量俯仰角。

大规模生产中实施的系统具有许多常见的解决方案：

信息由轮廓和背景的相对位置给出；
侧倾角的变化与轮廓相对于背景的角运动有关；
俯仰角的变化与轮廓相对于背景的线性位移有关。

但是很容易猜到可以以几种不同的方式实现所需的相对运动。经过上世纪的反复试验，航空发展留下了两个可行的组合：

1.固定轮廓，在滚动和俯仰背景下移动。使用的名称：“直接指示”，“从飞机到地面的视图”，较少使用“以自我为中心的指示”。

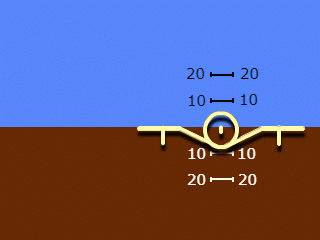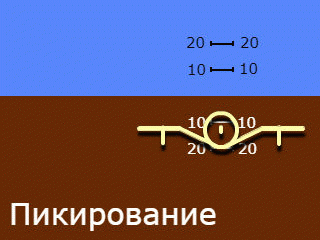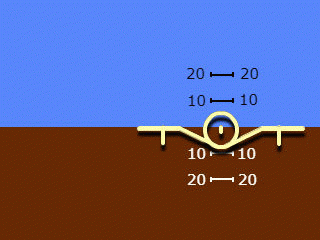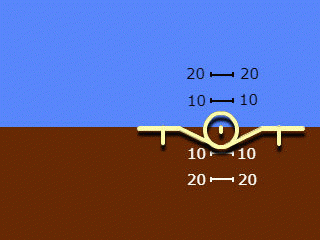
2.仅沿滚动方向移动的轮廓，仅沿俯仰方向移动的背景。使用的名称为：“反向指示”和“从地面到飞机的视线”，较少使用“地心指示”。

请注意，第2节的名称适用于整个系统，但仅反映了其中采用的侧倾角指示原理。在所使用的两个系统中，俯仰角指示均为“直线”和“以自我为中心”。

在现有的飞行模拟器（例如Microsoft Flight Simulator和Digital Combat Simulator）中，两种类型的显示都可以在操作中看到。

值得注意的是，并非所有已知的解决方案都适合上述模式。举一个超出指定框架的例子，让我们考虑两项发明专利：RU 2561311和RU2331848

。第一项专利专门针对“俯仰和横摇指示器高度隔开的人造地平线”，作者：V.I。Putintsev和N.A.Lituev。从专利。

如有必要，您可以在原始来源的文本中找到名称的解码和作品说明。...总体而言，发明的想法很简单：``从地面到飞机的视线''的想法既可以滚动也可以俯仰（完全的``地心指向性''）实现，但指示分为两个独立的组成部分。

第二发明具有更复杂的名称：“用于对飞机在空间中的位置和控制进行逻辑指示的飞行命令装置”。专利作者：A.P. Plentsov和N.A. Zakonova。俯仰和横滚指示的想法在这里相当不寻常。专利

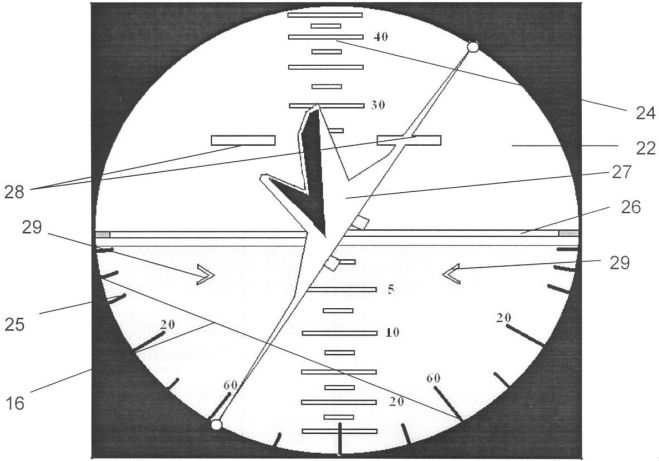
中给出了电路名称的说明，设备说明，与模拟的比较以及设计上稍有不同的附加电路。

与先前发明的共同点是两个通道的地心说。同时，与现有模型一样，人工地平线只有一个“飞机符号”，但这不再是轮廓，而是三维模型-“体积模型”。如果横摇运动与“反向”指示中实现的横摇运动类似，则此设备上的俯仰和俯冲看起来很原始。

实际显示系统设计中有许多阻碍创新的因素。例如，保守的合理理由之一是希望保持操作员所获得技能的连续性，包括感知信息的技能。电脑游戏可以提供更多的创造力，因此，在不深入研究解决方案的比较分析的情况下，我们将以看起来最有效的发明为基础。

解决方案要求

在开始编写代码之前，让我们定义任务：

1.必须编写drawAttitude（）函数，该函数根据A.P. Plentsov和N.A. Zakonova的发明使用画布绘制人工水平指示器。2

.该函数获取画布的上下文，坐标指示器的中心，侧倾角和俯仰角的值（以度为单位），指示器面的半径。

3.俯仰角的值限制为从负30度到正30度的间隔。

4.侧倾角的值限制为从负45度到正45度的间隔。

5.如果参数的值超出p中指定的值。3和4极限指示符显示最近的允许值。

功能创造

该功能代码包括以下部分：

1.检查输入的值是否超出限制。

2.将角度转换为弧度。

3.通过指示器半径的值缩放“布局”和字体的特征尺寸。

4.图纸部件：

a）指示器主体。

b）布局。

c）俯仰和滚动刻度。

下面的函数按此顺序编写，并且其各个部分由注释分隔。

完整的代码

index.html:

<!DOCTYPE html>
<html>

<head>
  <title>Attitude</title>
  <script src="js/attitude.js"></script>
</head>

<body>
  <canvas id="drawingCanvas" width="640" height="480"></canvas>
</body>

</html>

attitude.js:

window.onload = function () {

    let canvas = document.getElementById("drawingCanvas");
    let context = canvas.getContext("2d");
    
    let run = function () {
        drawAttitude(context, 320, 240, 30 * Math.sin(performance.now() / 2000), 45 * Math.sin(performance.now() / 5000), 200);
    }

    let interval = setInterval(run, 1000 / 60);
};


drawAttitude = function (ctx, centreX, centreY, pitch, roll, radius = 100) {
    //   :
    if (pitch > 30) pitch = 30;
    if (pitch < -30) pitch = -30;

    if (roll > 45) roll = 45;
    if (roll < -45) roll = -45;
    //  :
    roll *= Math.PI / 180;
    pitch *= Math.PI / 180;
    // ""  :
    let vehicleSize = radius * 0.8;
    ctx.font = Math.round(radius / 8) + "px Arial";
    //    :
    ctx.lineWidth = 2;
    ctx.strokeStyle = "Black";
    // :
    ctx.beginPath();
    ctx.arc(centreX, centreY, radius, 0, Math.PI, false);
    ctx.fillStyle = "Maroon";
    ctx.stroke();
    ctx.fill();
    // :
    ctx.beginPath();
    ctx.arc(centreX, centreY, radius, 0, Math.PI, true);
    ctx.fillStyle = "SkyBlue";
    ctx.stroke();
    ctx.fill();
    //"":
    ctx.beginPath();
    //:
    let topSideIsVisible = (pitch >= 0);
    ctx.strokeStyle = topSideIsVisible ? "Orange" : "Brown";
    ctx.fillStyle = topSideIsVisible ? "Yellow" : "Red";
    ctx.lineWidth = 3;
    //
    //  4 ,       ,
    //  :
    ctx.moveTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
    ctx.lineTo(centreX + vehicleSize * Math.cos(roll), centreY + vehicleSize * Math.sin(roll) * Math.cos(pitch));
    ctx.lineTo(centreX, centreY - 2 * Math.sin(pitch) * vehicleSize);
    ctx.lineTo(centreX - vehicleSize * Math.cos(roll), centreY - vehicleSize * Math.sin(roll) * Math.cos(pitch));
    ctx.lineTo(centreX, centreY - Math.sin(pitch) * vehicleSize / 2);
    ctx.stroke();
    ctx.fill();
    // :
    // :
    ctx.beginPath();
    ctx.strokeStyle = "Black";
    ctx.fillStyle = "Black";
    ctx.lineWidth = 1;
    //:
    ctx.fillText(30, centreX - radius * 0.28, centreY - vehicleSize + radius / 20);
    ctx.fillText(20, centreX - radius * 0.28, centreY - vehicleSize * 0.684 + radius / 20);
    ctx.fillText(10, centreX - radius * 0.28, centreY - vehicleSize * 0.348 + radius / 20);
    // - :
    ctx.moveTo(centreX - radius / 10, centreY - vehicleSize);
    ctx.lineTo(centreX + radius / 10, centreY - vehicleSize);
    ctx.stroke();

    ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.684);
    ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.684);
    ctx.stroke();

    ctx.moveTo(centreX - radius / 10, centreY - vehicleSize * 0.348);
    ctx.lineTo(centreX + radius / 10, centreY - vehicleSize * 0.348);
    ctx.stroke();
    // :
    ctx.beginPath();
    ctx.strokeStyle = "White";
    ctx.fillStyle = "White";
    //:
    ctx.fillText(30, centreX - radius * 0.28, centreY + vehicleSize + radius / 20);
    ctx.fillText(20, centreX - radius * 0.28, centreY + vehicleSize * 0.684 + radius / 20);
    ctx.fillText(10, centreX - radius * 0.28, centreY + vehicleSize * 0.348 + radius / 20);
    // - :
    ctx.moveTo(centreX - radius / 10, centreY + vehicleSize);
    ctx.lineTo(centreX + radius / 10, centreY + vehicleSize);
    ctx.stroke();

    ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.684);
    ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.684);
    ctx.stroke();

    ctx.moveTo(centreX - radius / 10, centreY + vehicleSize * 0.348);
    ctx.lineTo(centreX + radius / 10, centreY + vehicleSize * 0.348);
    ctx.stroke();

    // :
    ctx.lineWidth = 2;

    //+-15 :
    ctx.fillText(15, centreX + radius * 0.6, centreY + radius * 0.22);
    ctx.moveTo(centreX + 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
    ctx.lineTo(centreX + 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);

    ctx.fillText(15, centreX - radius * 0.75, centreY + radius * 0.22);
    ctx.moveTo(centreX - 0.966 * 0.8 * radius, centreY + 0.259 * 0.8 * radius);
    ctx.lineTo(centreX - 0.966 * 0.95 * radius, centreY + 0.259 * 0.95 * radius);

    //+-30 :
    ctx.moveTo(centreX + 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
    ctx.lineTo(centreX + 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);

    ctx.moveTo(centreX - 0.866 * 0.8 * radius, centreY + 0.5 * 0.8 * radius);
    ctx.lineTo(centreX - 0.866 * 0.95 * radius, centreY + 0.5 * 0.95 * radius);

    //+-45 :
    ctx.moveTo(centreX + 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
    ctx.lineTo(centreX + 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);

    ctx.moveTo(centreX - 0.707 * 0.8 * radius, centreY + 0.707 * 0.8 * radius);
    ctx.lineTo(centreX - 0.707 * 0.95 * radius, centreY + 0.707 * 0.95 * radius);

    ctx.stroke();
}

最难理解的是用于绘制“布局”的代码。让我们更详细地考虑它。作为布局，决定使用箭头形状的平面对称图形。

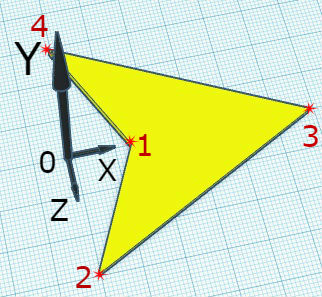
布局的顶部和底部表面的轮廓和填充颜色互不相同。选择当前的配色方案是代码的第一部分。

接下来是图形轮廓的构造。

最困难的任务是确定图形顶点在YOZ平面上的投影坐标。这就是具有三角函数的表达式所解决的。代码中的顶点按照图中的编号顺序遍历。

该代码的最大部分专用于比例和签名。比例标记有很多差异：顶部和底部，左侧和右侧，带有和不带有标签。令人印象深刻的行数是由于为每个元素编写了“个体”代码。

相应角度的三角函数用于施加滚动标记。由于每个标签的角度值都是事先已知的，因此将正弦和余弦的现成值写入代码中。

最好评估动态指标的类型。我们借助新功能展示了俯仰和侧倾振荡。对于最大的位置变化，让我们使振荡幅度与指标极限相对应，并且使周期不同且相互简单。

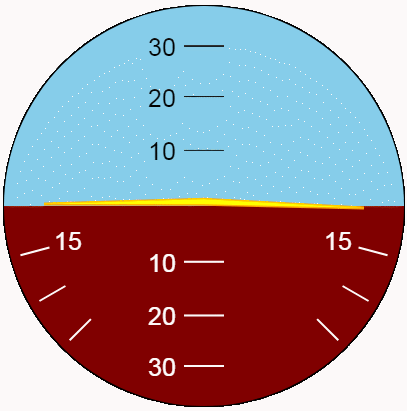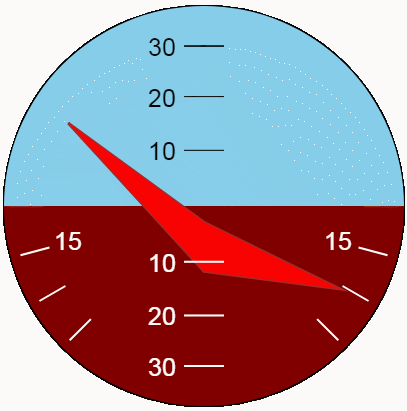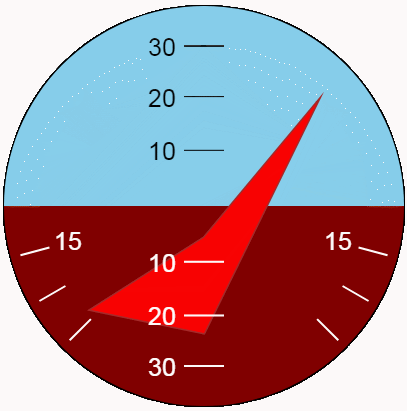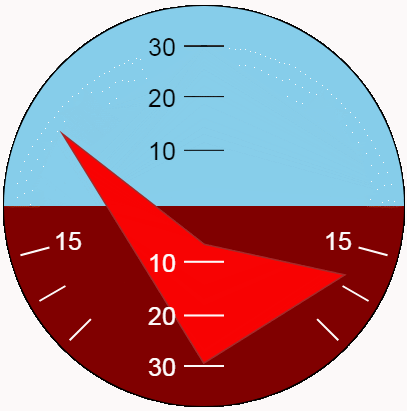
结论

严格来说，上述用于侧倾和俯仰可视化的代码应被称为“基于” A. P. Plentsov和N. A. Zakonova的发明的指示，与原始方案有所不同以简化问题，而另一些偏离则可以改善实施。

提出的指标在设计方面远非理想。根据任何客观标准，显示值的可接受限制不是最佳的。但是，创建有趣的技术演示程序的任务可以认为已经解决。

HTML5画布上的人造地平线指示器

人工视界的目的和范围

已知的可视化技术

解决方案要求

功能创造

结论

More articles: