使用神经网络控制机器人复合体的多链接机械手

介绍

在模拟机器人的运动控制系统时，需要解决其执行器的运动学和动力学问题。运动学存在一个直接的逆问题。运动学的直接问题是通常通过广义坐标的已知值来确定机器人操纵器工作工具特征点的空间位置和方向。与直接问题一样，运动学的逆问题也是运动学分析和综合的主要问题之一。为了控制连杆的位置和操纵器的作业工具的方向，有必要解决运动学上的逆问题。

就计算程序而言，用于解决逆运动学问题的大多数分析方法都非常昂贵。一种替代方法是使用神经网络。输入数据。考虑具有表1中所示参数的三链接操纵器。

表1-三连杆机械手的DH参数

在MatLab环境中，使用免费的Robotics Toolbox，可构建三连杆机械手的计算机模型。下面是MatLab脚本的一部分，其中我们将表1中的参数A，Alfa和D的值分配给了L数组。我们将Tetta参数分配给变量'initialPose_left'-机械手的初始位置。 

function [L,initialPose_left,baseL] =model3z 
%   
initialPose_left = deg2rad([0 0 0]); 
L(1) = Revolute('d', 0.2, 'alpha', pi/2, 'qlim', initialPose_left(1)+deg2rad([-90 +90]) ); 
L(2) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-20 +90]));   
L(3) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-90 +90])); 
% -178 +178 
baseL = [1 0 0 0;  
        0 1 0 0;  
        0 0 1 0;  
        0 0 0 1]; 

1 (. 1) . 

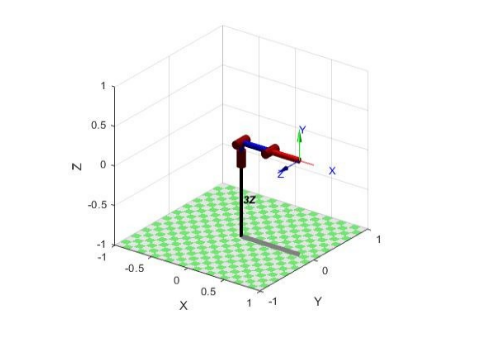
 Tetta, .  initialPose_left. 

. , . 

, .  

  . :

q – . 

%       
t1_min = L(1).qlim(1); t1_max = L(1).qlim(2);  
t2_min = L(2).qlim(1); t2_max = L(2).qlim(2); 
t3_min = L(3).qlim(1); t3_max = L(3).qlim(2); 
%     
t1 = t1_min + (t1_max-t1_min)*rand(N,1); 
t2 = t2_min + (t2_max-t2_min)*rand(N,1); 
t3 = t3_min + (t3_max-t3_min)*rand(N,1); 
Y = horzcat(t1, t2, t3);

, .  : 

:  x,y,z – . R – , . 

%    4x4 
T = zeros(4, 4, N); 
T(:, :, :) = leftArm.fkine(Y); %  ,       
%R = tr2rpy(T(1:3, 1:3, :), 'arm'); %      
R = tr2eul(T(1:3, 1:3, :)); %      
Tx = reshape(T(1, 4, :), [N 1]); %  - 
Ty = reshape(T(2, 4, :), [N 1]); 
Tz = reshape(T(3, 4, :), [N 1]); 
% scatter3(Tx,Ty,Tz,'.','r'); 
X = horzcat(Tx, Ty, Tz, R); %   

. 3.2.1  , 3000 . 

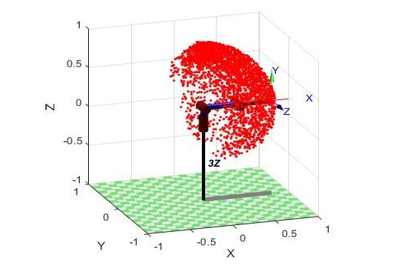
, 3000 . , X Y. 

, .

Keras Python. .

X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.2,
random_state=42) 

« » . .

def base_model():
 model = Sequential()
 model.add(Dense(32,input_dim=6,activation='relu'))
 model.add(Dense(64,activation='relu'))
 model.add(Dense(128,activation='relu'))
 model.add(Dense(32,activation='relu'))
 model.add(Dense(3, init='normal'))
 model.compile(loss='mean_absolute_error', optimizer = 'adam', metrics=['accuracy'])
 model.summary()
 return model

, . . , , . , , .       KerasRegressor,  Keras.

clf = KerasRegressor(build_fn=base_model, epochs=500, batch_size=20,verbose=2)
clf.fit(X_train,y_train) 

.

res = clf.predict(X_test) 

99% , . 

3 , , , . . , . . - . , , , , .

%%    ,    
M=[-178:10:178]; %      -178   +178    10 
M_size=length(M); 
first_q=zeros(M_size, 3); 
T33 = zeros(4, 4, M_size); 
T34 = zeros(4, 4, M_size); 
first_q(:,1)=[deg2rad(M)]; %  q 
T33(:, :, :) = leftArm.fkine(first_q);%      ,   
R = tr2rpy(T33(1:3, 1:3, :), 'arm'); %      
Tx = reshape(T33(1, 4, :), [M_size 1]); %  - 
Ty = reshape(T33(2, 4, :), [M_size 1]); 
Tz = reshape(T33(3, 4, :), [M_size 1]); 
plot3(Tx,Ty,Tz) 
axis([-1 1 -1 1 -1 1]);hold on;grid on; 

XX = horzcat(Tx, Ty, Tz, R); %        
T34(:, :, :) = leftArm.fkine(q_new); %     ,   
Tx2 = reshape(T34(1, 4, :), [M_size 1]); %  - 
Ty2 = reshape(T34(2, 4, :), [M_size 1]); 
Tz2 = reshape(T34(3, 4, :), [M_size 1]); 
plot3(Tx2,Ty2,Tz2,'.') 
axis([-1 1 -1 1 -1 1])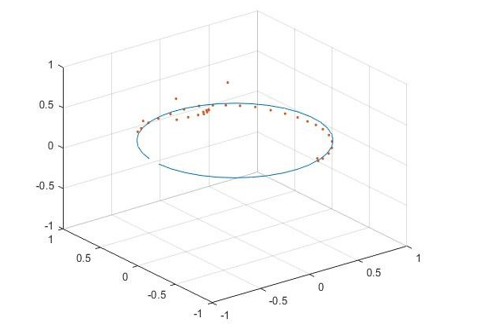 

. . , - . , . . «Programming by demonstration», . Matlab , – .