NaN可能仍然会让您有些惊讶

起初，我认为这只是面试中可能要问的另一个问题。大概，如果您正确地使用大脑，您就可以猜出结果是什么。他靠在椅子上，开始思考，打开逻辑，记住要依靠推理的东西。但是徒劳！突然，很明显找不到答案。但为什么？您需要了解什么才能找到它？在数学上？用编程语言？



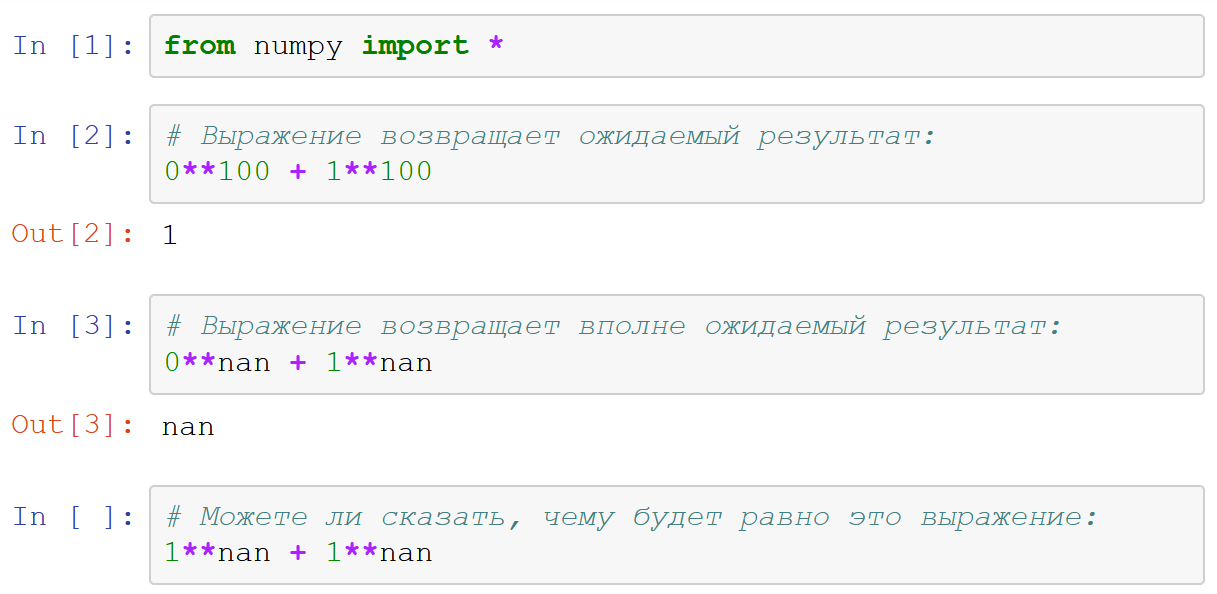
答案应该是NaN。但是为什么我不确定呢？一直以来，我相信任何包含NaN的表达式都将返回NaN。好吧，也许只有将NaN除以零-在这种情况下，将引发ZeroDivisionError异常。百分之一百的NaN！



我将表达式输入记事本的单元格中：

>>> 1**nan + 1**nan
2.0

确实？等待：

>>> arange(5)**nan
array([nan,  1., nan, nan, nan])

也就是说，由于某种原因，NaN幂的一个为1，但NaN幂为零，所有其他数字均为NaN。逻辑在哪里？怎么了？



因此，让我们再次去：

>>> 0**nan, 1**nan
(nan, 1.0)

也许只是因为缺乏对NaN的深入了解的实际需求，我只是没有怀疑什么？也许我知道，但是忘了？甚至更糟-我不知道并且忘记了吗？



我们去维基百科。在那里，这个问题也被指定为问题，但是为什么没有这样解释一切。但是我了解到：

>>> hypot(inf, nan)
inf

虽然，同时：

>>> sqrt(inf**2 + nan**2)
nan

您知道，这也有些奇怪。



好的，我们从Wikipedia转到第182页的C99，最后得到了一个逻辑解释，为什么pow（x，0）对任何x都返回1 ，即使x等于NaN：

>>> power(nan, 0)
1.0

如果功能 $$$f(x)$ 被提升为力量 $$$g(x)$ 并且其中 $$$g(x)$ 趋于0，则结果将为1，无论值是多少 $$$f(x)$...







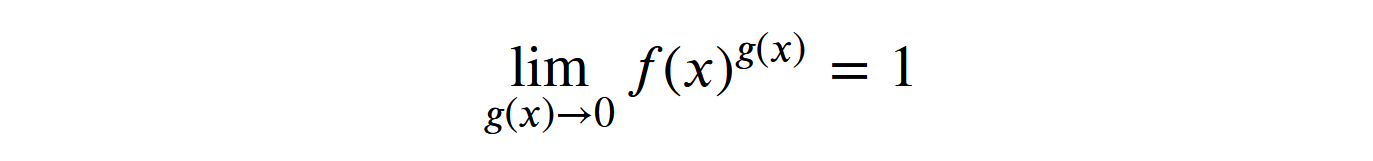
如果结果不取决于函数的数值$$$f(x)$，则1是有效结果，即使对于NaN也是如此。但是，这仍然不能解释为什么NaN幂为1的原因是1。我们



寻找另一个C99，在461页上没有看到任何解释，只是要求pow（+1，y）应该对所有y返回1 ，即使相等NaN。一切。



另一方面，解释为什么pow（NaN，0）= 1比pow（NaN，0）= NaN更可取，这仍然表明NaN不应从字面上理解为非数字...假设，通过一些计算，我们得到的数字超过了为此数字类型分配的内存大小，例如：

>>> a = pi*10e307
>>> a
inf

结果，我们得到了inf，这个数字到底是什么我们不知道，但仍然是某种数字。然后，我们一次又一次地计算出一个太大的数字：

>>> b = e*10e307
>>> b
inf

a和b 之间的差异将返回NaN：

>>> c = a - b
>>> c
nan

我们可以将c视为非数字的唯一原因是因为我们没有使用足够精确的计算。但是，在c中， NaN下方仍然隐藏着一些含义。我们不知道这是什么意思。但是它仍然是一个数字，并且由于这是一个数字，因此pow（1，NaN）= 1并不足为奇。



为什么然后pow（0，NaN）= NaN？事实是，如果我们将0提高到任意幂，那么我们实际上会得到零。一种情况除外-度为0时：

>>> 0**0
1

因此，在表达式pow（0，NaN）中，NaN的特定值存在歧义。当然，可以在NaN下隐藏0的可能性很小，并且可以假定pow（0，NaN）= 0。但是，尽管如此，最好还是放心使用，因为您永远都不知道会导致什么。也许这就是标准制定时的推理方式。



我什至不知道该说些什么...如果您事先知道答案，那么很可能会被您羡慕，因为可以将这些知识派上用场的领域可能充满了有趣的任务。反之亦然。在评论中写出来。



PS由于NaN指的是浮点数，因此它可以是字典键：

>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'

在实践中使用它有意义吗？我认为这不值得。