在第一部分中,我们研究了外部代数,并意识到3D中的法线向量可以解释为双向量。通常,要转换双矢量,您需要一个不同于转换普通矢量的矩阵。使用双矢量的规范基础,我们发现这是伴随矩阵,与逆转置成比例。这种推理至少部分地解释了为什么法线被逆转置矩阵变换。
但是一些问题被扫到了地毯下。
我们考虑了伴随矩阵,但没有显示它们与代数证明如何转换平面方程有关需要逆转置矩阵。从某种意义上说,矩阵之间的比例是牵强的。
而且,我们看到了 来自外部代数的向量为向量几何对象提供了自然的解释,其中包含长度,面积和体积的单位,这些单位在缩放时会相应更改。但是,对于密度,我们找不到类似的东西-与长度,面积和体积成反比的单位。
在本文中,我们将讨论完成绘画所需要的另一个几何概念。将这个新概念与已经研究过的外部代数相结合,将阐明并解决剩余的问题。
作为向量
本文的大部分内容将重点放在接受和返回各种类型的向量的函数上。要了解它,您需要做一些精神上的翻筋斗,如果您以前从未遇到过,这似乎是违反直觉的。
在这里是:返回向量本身的函数是向量
乍一看,这种说法似乎毫无意义。向量和函数是完全不同的事物,例如苹果和...椅子,对吗?函数从字面上看如何可以是向量?
! . , : . , , .
: ( , ) — . . , , "". .
, , . , .
( : , . !)
(3D) (2D), / , . :
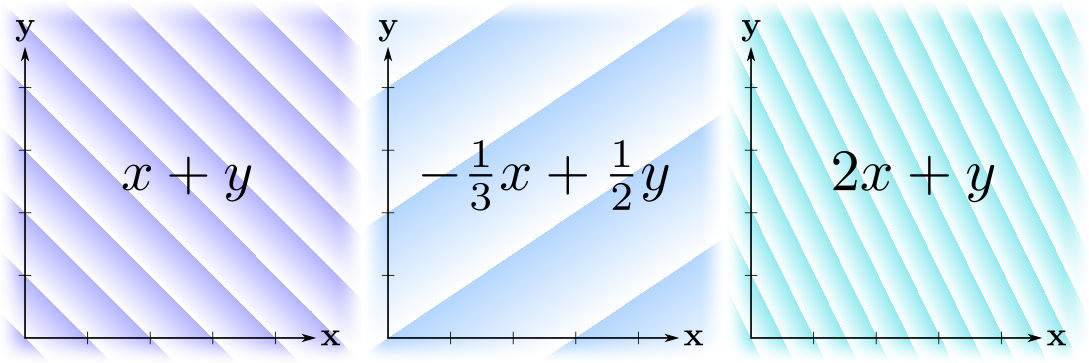
— . . , "́" ( ́ ) , .
, . , .
, — , , . - , , . , , .
, . . , — — , :
, — !
, : . .
, , , . , , "" . , — , … .
: . — , — . , . , — , .
:
, " " , .
. , , . :
. :
.
, , , . , . , . .
:
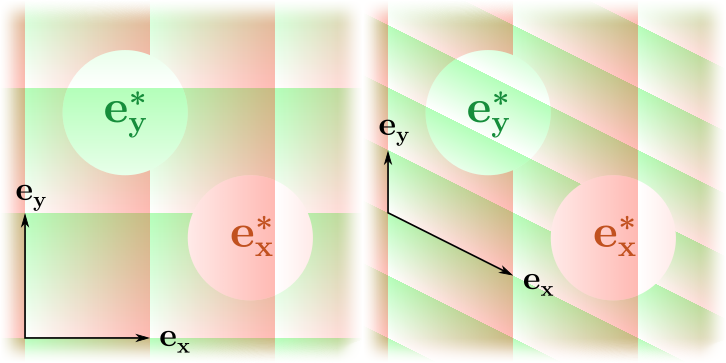
:
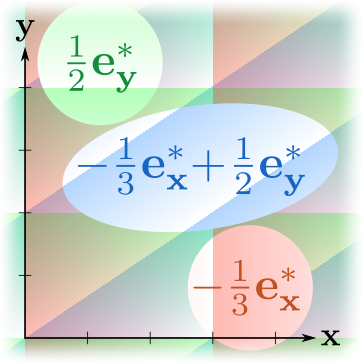
. :
, ( ), , , .
! "" ( ), ( 3D), ( ). !
— , . ?
: . , . : - . ( , ).
: , , . :
, , .
, . " " : .
, , . , . .
, . , ?
, , . , :
! , . "" "" . , , !
, . , (, , , //) - . ( ), " "" ?"
"". , , - , . .
. , , — , . .
. , :
:

? : .
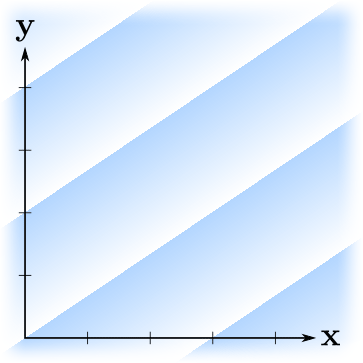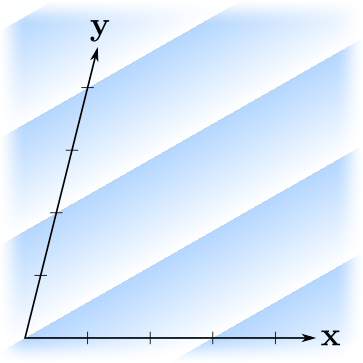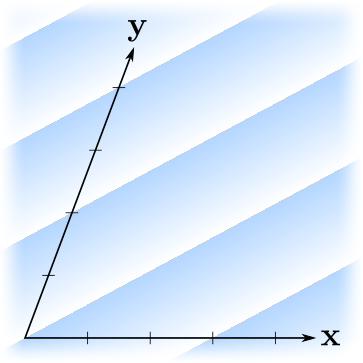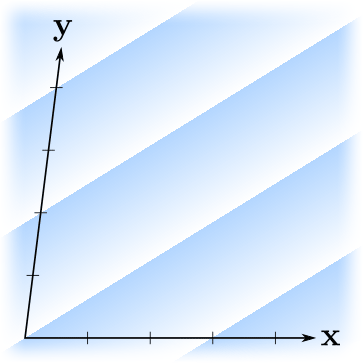
, ? . , — . ?
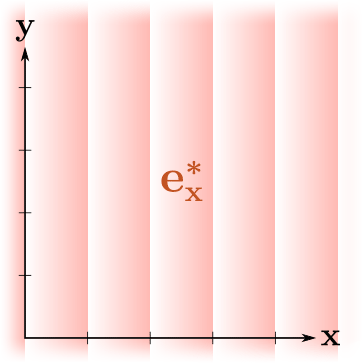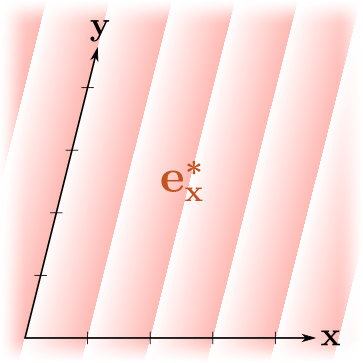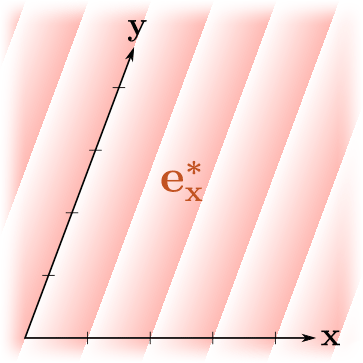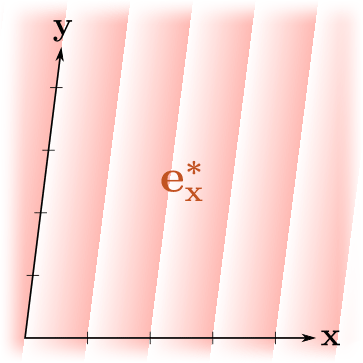
, ! , , , "" , . , .
, . , , , ,
!
, , . , , ( ), . :
.
, , .
?
, — 2D 3D. , , :
.
, , . :
, .
, , .
. , , , ? ?
, . " " , , . , : , . : , — .
这就是我想谈谈法向向量的变换的全部内容,但是还有更多问题待解决。在第一部分的结尾,我问了一个关于负规模的问题。现在我们减去了一级,但是-2和-3呢?为了理解这一点,我们必须将外部代数和对偶空间相结合,这将在第三部分中进行。