
可能每个人都面临这样一个事实,即他们不得不面对一些艰巨的任务,即使是在长时间的顽固工作或几天之后,也无法立即找到解决方案。今天,我们将讨论这类问题中的一类-NP完全。
总的来说,在日常生活中完成这些任务是否现实?实际上,它们出现在很多情况下:组合图,图和网络,逻辑公式的执行,使用图,最佳加载,图,离散优化问题,找到最长的序列,找到相等的总和以及许多设置问题!这不是完整的列表。
切入点之下是一个非正式的指南-如何理解您面前可能会有NP问题,以及如果事实确实如此,该怎么办。今天,我们从实际的角度对这个问题进行攻击。
确保她真的在你面前
您怎么知道什么时候遇到NP完全问题?首先,最简单的启发式检测通过已知的NP完全问题,以确定类似的东西,有很多这样的列表,搜索例如。
其次,考虑任务的以下属性:
- 我们需要从空间exp(n)中选择n个元素的解决方案
- 如果您已经从该空间获得了长度为n的解,则可以轻松地(按多项式)检查它
- 决策要素之一的选择(可能)会影响所有其他要素(不一定是全部)的选择。
- 在最坏的情况下,可以始终枚举选项,并通过简单的枚举考虑整个指数空间。
- 参数n-解的长度或空间本身不具有固定值,也就是说,我们不是在谈论始终固定的8 x 8棋盘,而是关于N x N问题的一般形式。
在这里和这里 阅读有关NP完全问题的性质的更多信息。
此清单上的工作示例
让我们举一个关于最近被批准为NP完全问题的简单例子!
根据文章的材料。您需要将N个皇后放在大小为N乘N的板上,前提是板上已经放置了K <= N(图片来自原始科学文章)
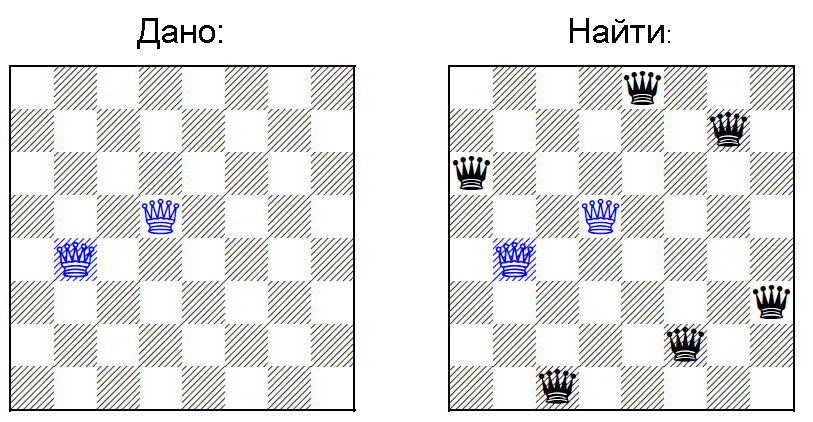
首先,请注意,部分约束的拉丁方NP的非常相似的问题是完整的。
然后我们遍历列表:
- 您需要从空间exp(N)(= N ^ 2 *(N ^ 2-1)* ....)找到N个皇后。
- N个皇后的解决方案很容易检查-对于每个皇后,您都需要检查对角线,垂直线和水平线。
- 设置一个会使其他多个选择无效-即 解决方案的要素之间存在依赖关系(您不能独立安排皇后区)。
- 在这里,您可以用蛮力解决exp(N)中任意选择的板的问题-我们将第一个放在(i,j)位置的第一个板上,将第二个放在其他任何空置的板上,依此类推。回溯保证找到解决方案。
- 该问题没有固定的参数-即,它以一般形式表示,并且随着N的增加,复杂度也随之增加。
请注意,如果始终知道主板是干净的并且任务变得微不足道,则列表中的一项会失败。
而且,这是一种有条件的实用方法-一种用于检测NP完全问题的启发式方法(具有所有优点和缺点)。
混合
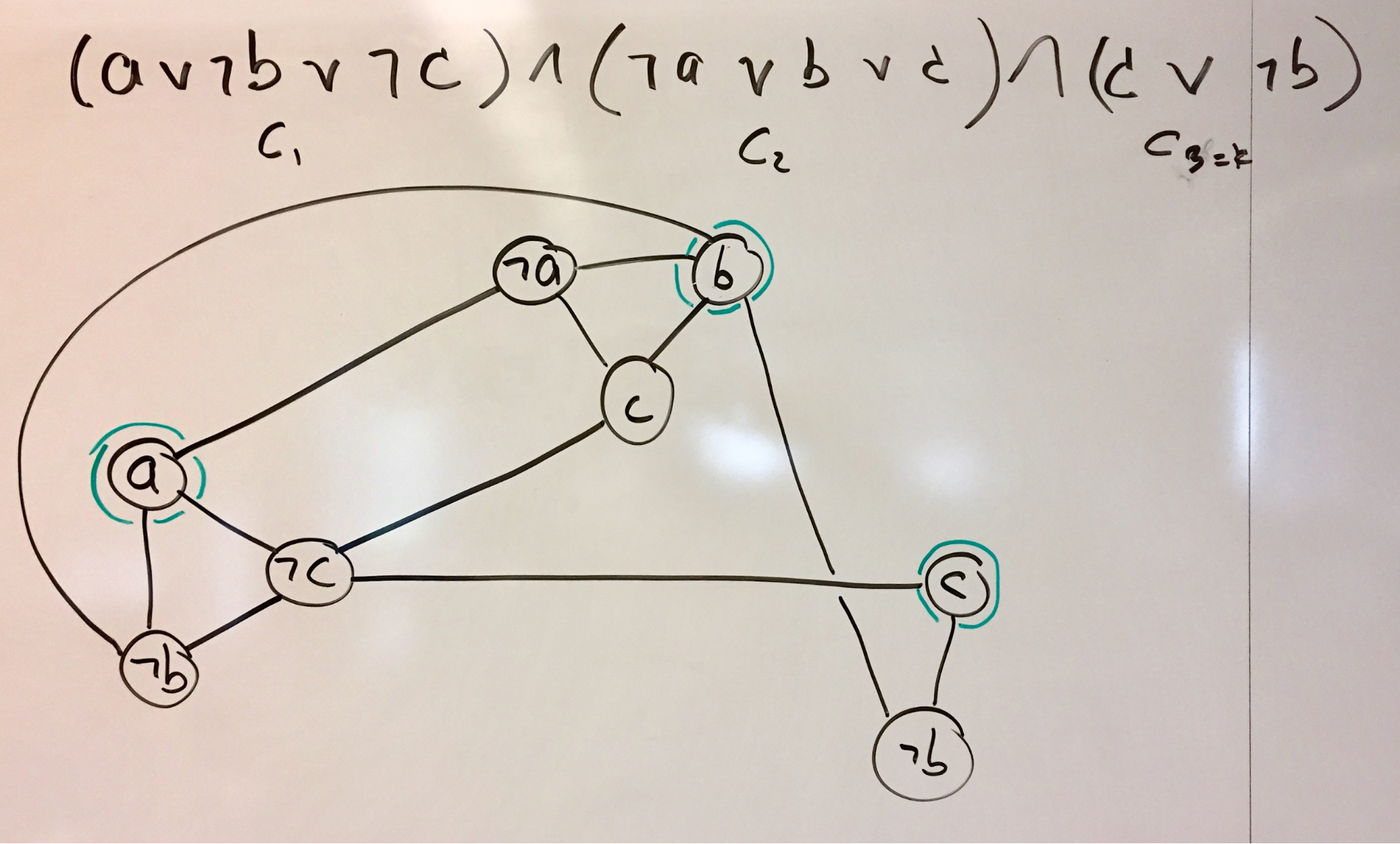
资料来源
为什么在手头上遇到类似的问题,在形式上很难理解我们正面临NP问题?我们确实需要向我们提出一个NP问题,然后我们将确定我们的问题是NP难题!而且,如果我们能够像上面的列表中那样模拟它,那么它就完整了-即至少NP并且不超过NP,实际上是“ NP问题中最难解决的问题”(与NP其余部分一样)。
好吧,我们需要吗?毕竟,如果直截了当,直截了当,您就面临一个NP问题,那么,如果您不写科学文章,就不需要证明任何事情。
而且您也需要(我们将在下面讨论):
- 使用可解决此类任务的系统模拟您的任务;
- 找到适合您情况的解决方案;
- 找到一个满足我们的近似解决方案。
不要放弃!
最重要的是评估尺寸参数和实际方案!
xkcd.com/287
例如,您知道尽管参数的值不是固定的,但并非在所有实际情况下都实现条件N <100,这意味着条件枚举可能对您来说是一个真正的解决方案。
您需要自己确定:参数的真正值是可能的并且真正地进入系统中,数据的一般分布和特征是什么,什么是真实的,什么不是?我们需要最优化的解决方案吗?让我们看一下这些要点。
输入数据的分配
或尽管在一般情况下输入数据可以是任意数据,但对于皇后的例子又是这样-通常一个皇后是固定的,甚至没有。这意味着您有90%的时间可以使用非常简单的解决方案,并且仅在极端情况下才调用复杂的解决方案。
平均而言,所有通常的组合都很简单:一个补充皇后的问题-我们知道有条件的DFS +启发式方法在大多数情况下可以非常快速地找到解决方案,并且只有在非常非标准的情况下才非常困难。

这是一个示例,说明如何针对使用逻辑编程技术对整个此类问题进行建模的通用方法,评估非常专业的NP完全平铺问题的解决方案:
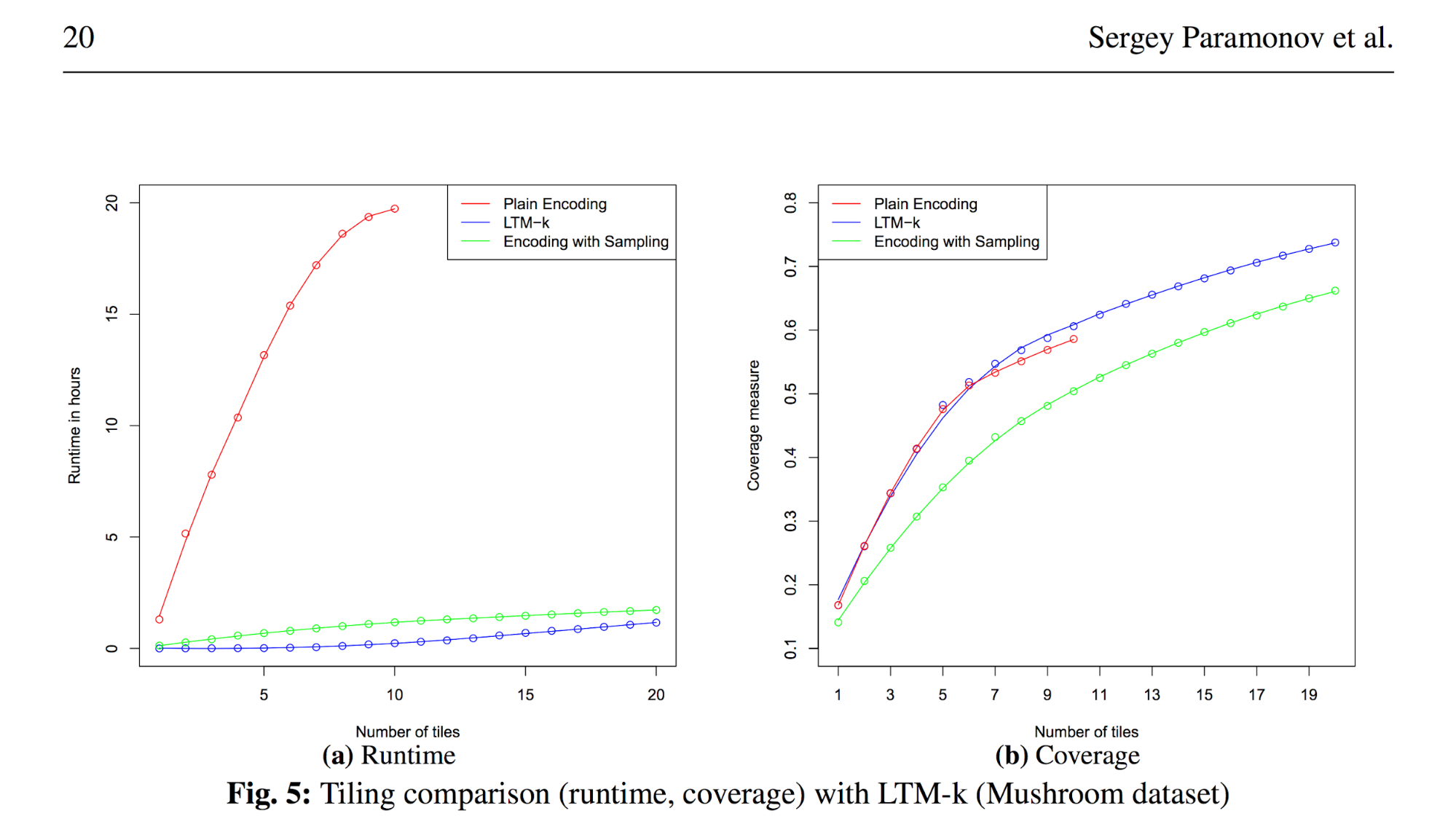
(摘自《关系数据分解》(Paramonov,Sergey; van Leeuwen,Matthijs; De Raedt,Luc:关系数据分解,机器学习,第106卷))
首先,特殊LTM-k解决方案的速度与通用方法有很大不同。因此,仅针对此类问题的基于启发式的解决方案就可以完全解决该问题。
其次,通过牺牲解的质量,通用逼近方法的速度非常相似。
启发式和近似
最后也是最强大的工具是使用NP完整的问题建模系统,例如Answer Set Programming。
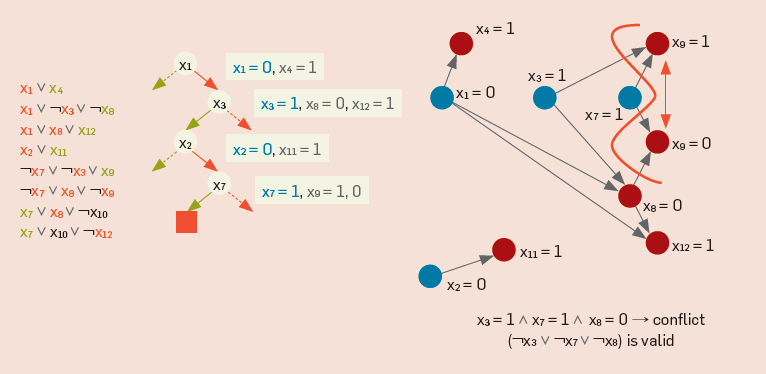
有关逻辑编程语言的更多信息。
例如,皇后布局问题的解决方案将如下所示:
% domain
row(1..n).
column(1..n).
% alldifferent: guess a solution
1 { queen(X,Y) : column(Y) } 1 :- row(X).
1 { queen(X,Y) : row(X) } 1 :- column(Y).
% remove conflicting answers: check this solution
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 == Y2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 + X1 == Y2 + X2.
:- queen(X1,Y1), queen(X2,Y2), X1 < X2, Y1 - X1 == Y2 - X2.
进行了简单的实验以找到不同数量的皇后N的解,我们得到了以下结果:沿X轴-皇后,沿Y-每秒的时间来寻找解决方案:
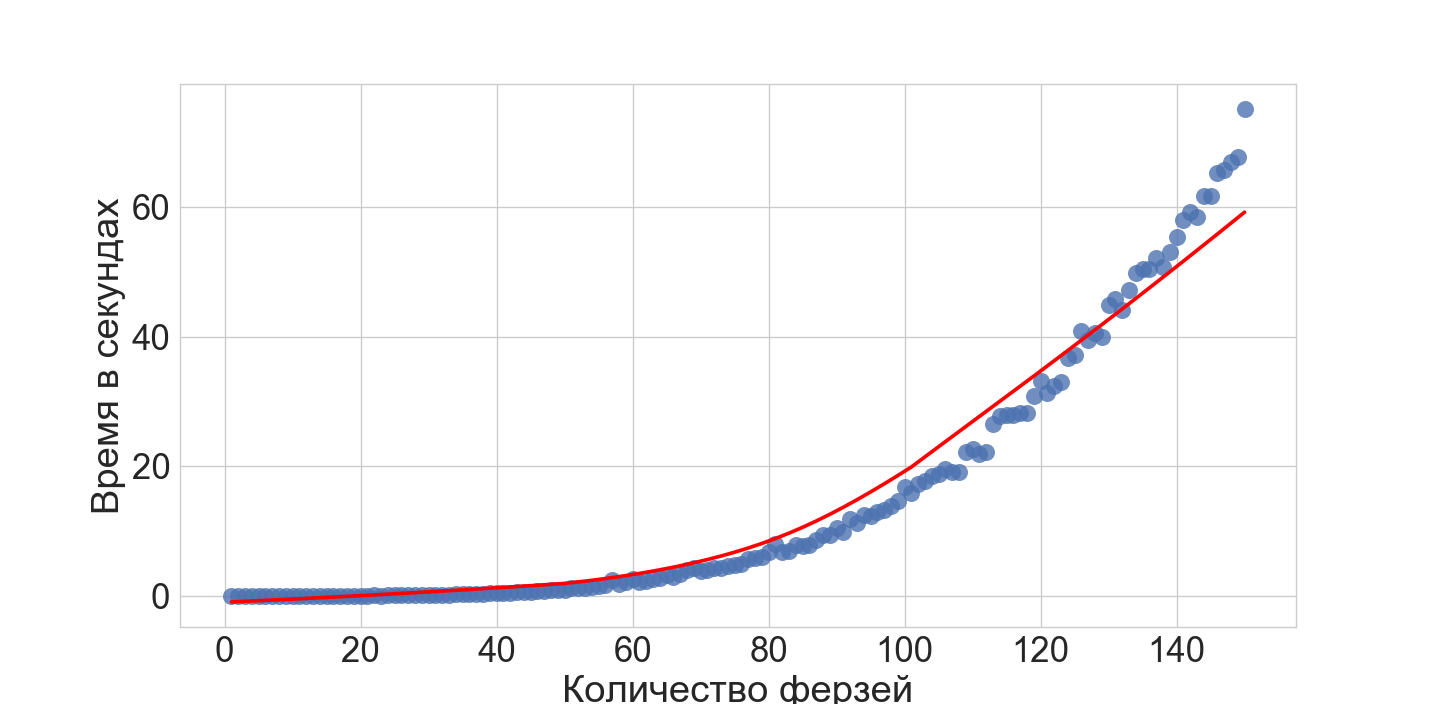
我们看到,尽管时间的增长显然不是多项式的(这是合乎逻辑的),但我们在有足够数量的皇后和董事会人数方面做得很好。
然后,如果我们知道什么板子尺寸对我们来说是真实的,我们就可以了解在实际系统中该精确解决方案对我们而言是可接受的。
结论
让我们以清单的形式仔细阅读文章中的想法
- 确定您确实有NP问题。
- 了解什么是现实的参数值和数据分布。
- 尝试编写(顺序取决于开发人员和/或任务):
- 准确的启发式解决方案(基于我们的分析)-足够快吗?
- — ?
- NP- — ? , CPU ? .
- : , .
- — , — . !
:

