关于线性变换,存在一个如此神秘的事实:其中一些变换,即非均匀缩放和剪切,由于某种原因会区分“普通”矢量和法线。当我们通过矩阵变换“法线”矢量时,由于某种原因,法线需要通过逆转置矩阵进行变换。如何理解呢?
通过简单的计算,您可以确保逆转置矩阵保持法线与其切平面的垂直性。在某种程度上,这种证明是足够的,但它错过了有关其背后所有几何结构的更深层且更有趣的故事。这是我想在接下来的几篇文章中讲述的故事。
单位和比例
在深入探讨本文的核心内容之前,这里有一个简短的摘要。考虑良好的旧均匀缩放比例(所有轴上的一个因子)。很难想到更无害的变换-只是所有向量乘以相同的数字。
但是,经过仔细检查,这里发生的事情并非完全无关紧要。某些数量带有物理“尺寸”或“单位”,例如长度,面积和体积。缩放时,这些值会根据其单位变化。有些值通常是``无量纲的'',缩放后不会改变。
例如,让我们列出在三维空间中缩放时所有可能的单位行为。我们将比例因子表示为... 然后:
- 无量纲数字不变,换句话说,它们乘以...
- 长度乘以...
- 面积乘以...
- 体积乘以...
但这还不是全部:密度也随比例因子的倒数而变化: - 线性密度乘以...
- 面积密度乘以...
- 堆积密度乘以...
密度可以表示诸如每长度纹理像素的数量,几何概率或体积中的粒子数量之类的东西。如果3D模型在增加的方向上按比例缩放,并且纹理的大小不变,则其texel密度会降低,依此类推。
, ( ) , : , ( ), , - . , -3 3. , - , .
( , . , 3D.)
, - . ? ? ? -, .
, . , . , Geometric Algebra for Computer Science. .
— , , , , . -, — . , — . .
— ( ) , . , , . , .
, , . , . , . , , , .
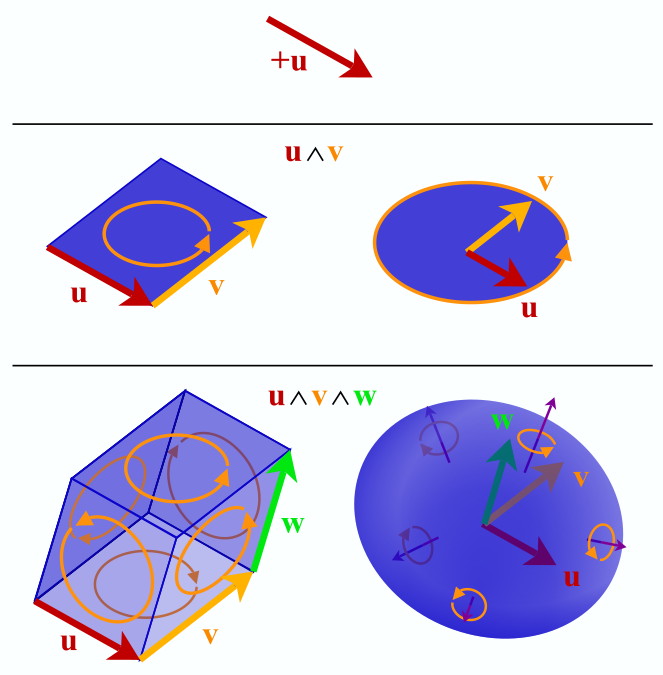
, — , , . , , , , .
. , , . , , "" "", "" "". , , .
́ , . , - . .
-
, . , , :
, , , , . :
— , . . , , . " " , .
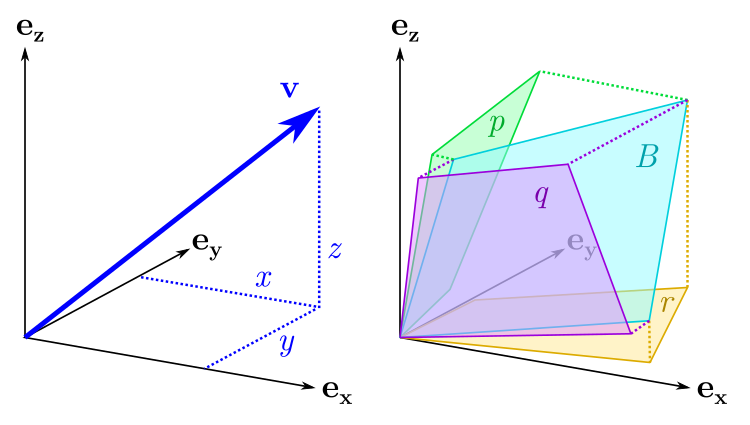
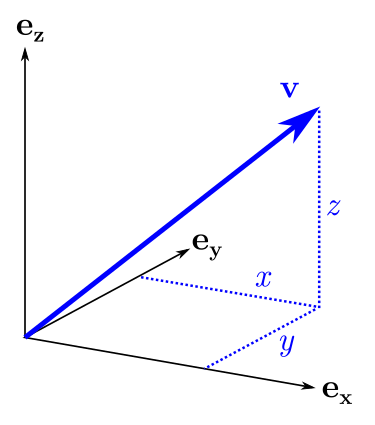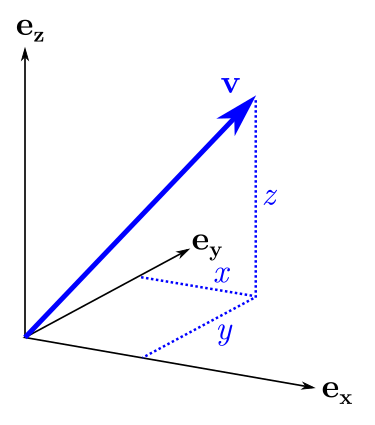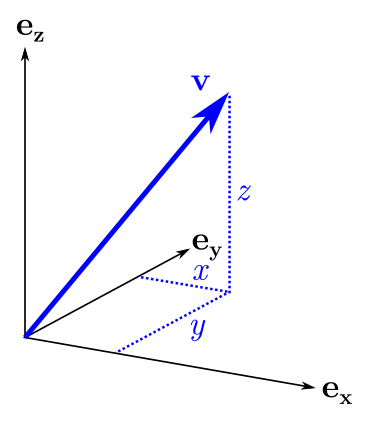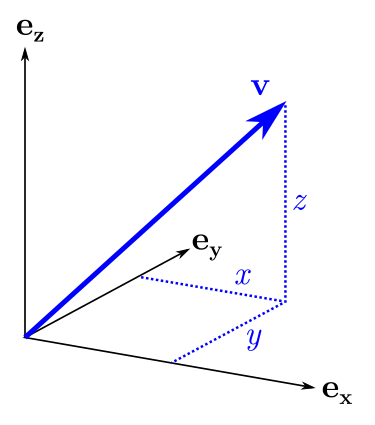
:
, 3D , : "" . — .
, : ( 1), ( 2) ( 3). 0. , , , . , , :
, , . , ( ).
, "" . , , . , .
, , .
" ", , , .
, . . :
, . :
. -, : . , . , . , .
3 . , .
-
, , — , — . ?
, , - . , . , , .
, :
, , , , , .
? ( ), . . , , :
! , , , .
, . , - . :
. , ?
, . 3 , . :
: 3, . , : , , — .
? . , "" . , . : , , , , , .

, . , , :
, . :
: , 3, .
, :
, , , :
, , . : .
: :
?
— , . .
. - - :
- . .
- .
- , . !
, .
, ? . , , . , . , , !
- , , , . , , . , , .
( , . . .)
, , - . , - - , .
. . : 3D. , — !
. , . , :
, , . , , , .
:
. , , (, ). , , . . , .
! , .
, - . — . ( ) " ".
, . , "" , . ? , , ? , , ( ). .
: , , -3 3. , - 0到3。但是,缩放比例为负的矢量单位呢?它们存在吗?如果是这样,它们是什么?
在下一集中,我们将进行更深入的挖掘,使我们的几何故事更加复杂。