什么?做什么的?
你好!
我想考虑一个计算几何问题,即构建凸3D船体。在我看来,这既不是最复杂的算法,也不是最简单的算法,它对于分析非常有用且有用。
如果您从未遇到过这样的任务,那么我想了解它,这将是一件很有趣的事情。
如果您刚刚听说过有关凸包的信息,则可以了解更多有关它们的信息。
如果您是凸包的专家,您可能想再次听听解决一个有趣问题的方法。
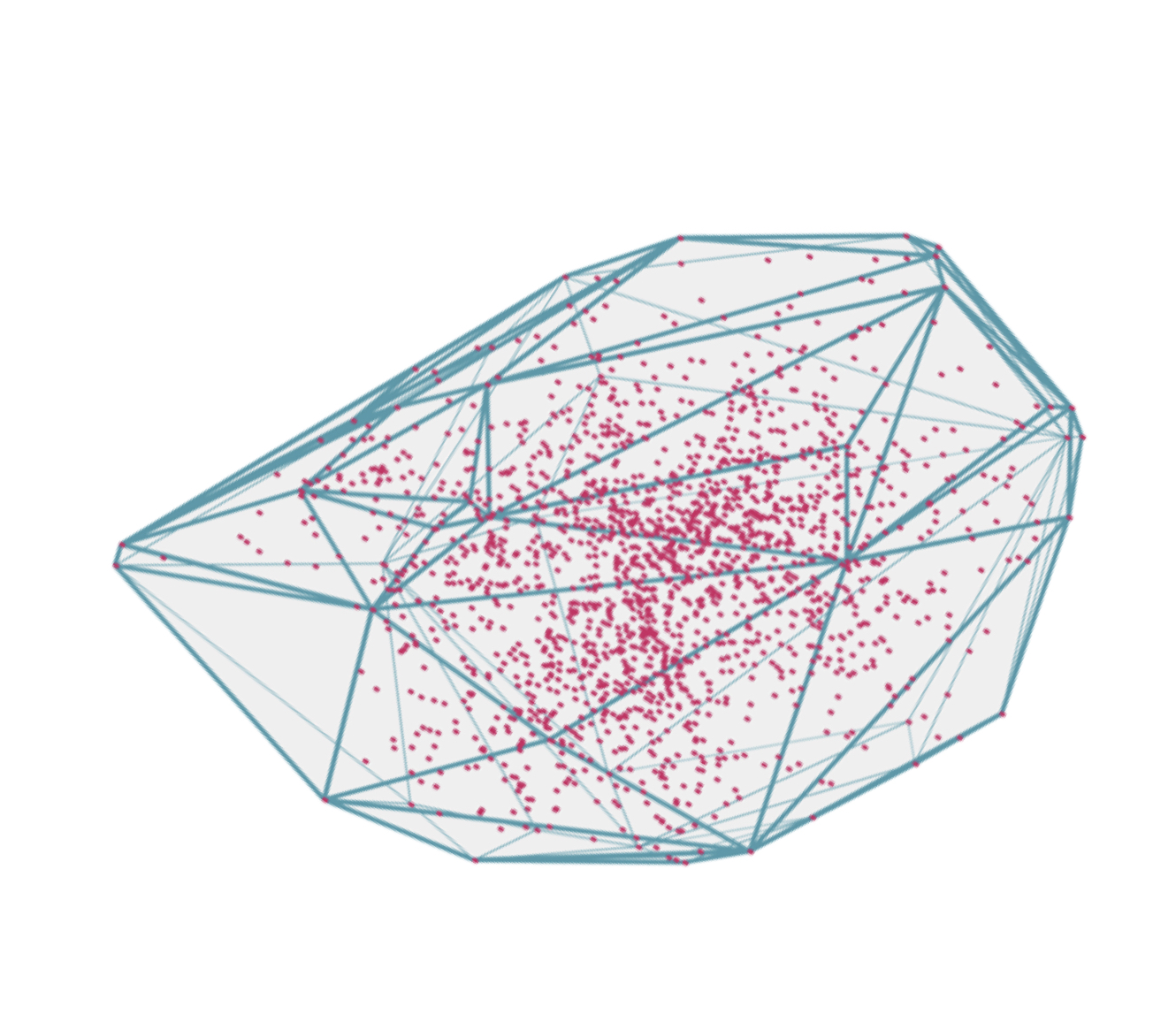
内容
- 什么?做什么的?
- 什么是凸包?
- 常用的词
- 算法说明
- 渐近性
- 算法实现
- 全面实施
我表示感谢 无印良品4ok 在撰写和编辑文章方面提供帮助。
什么是凸包?
X集的凸包是包含X集的最小凸集。
严格,但不是很清楚。现在,我将尝试通过一个例子来告诉您:
想象一下平面上的一组点,假设我们想知道为了使其余点集位于轮廓曲面内必须连接的最小点数是多少。这是找到最小凸包的问题。

2D
,
, , , , , , "" , .
, , , 3D . , .
: , ?
— .
— . , , : .
, , .
, ( ) " ".
, 4 . 3 .
, , .
, , 3d , . , .
1.
, , , , .
, .
Z. , , "" Z . XY , . . , . P, , "" — f.
, . Q, f ( prQ). , () {P, Q} {Q, prQ} — — . , Q , . Q .

. R, , P, Q R (0, 0, 1) . , f — XY. , , . , , R .
, , , , ( - ).
, P, Q, R .
-! , .
2.
, , , . , .
: , . , , , , () ( ), , . , , , , .
: , . : .
1. ? , . . E. , , E — R. ( E) , E R. , , , — .
2. , , " ", E , , E .
3. , , . , , . , , , .
4. , . , . , "" , .
5. , "" , .
6. , . , .
, ( ), 3D .
, , . , . N, H , O(NH). H 2N, O(N^2).
, , , O(NlogN), , . 2D , O(NlogN), , , , .
, , : .
, , , , , . C++.
. . , , -. - . ( , ).
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point (coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator- (const Point& other) const;
Point operator+ (const Point& other) const;
bool operator!= (const Point& other) const;
bool operator== (const Point& other) const;
};. 22 ( ).
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}( A — — - - AB AC):
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}( ):
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}:
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}, .
. , . , , , , . , , .
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false; // , ?
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)) :
first(first), second(second), flatness(flatness) {}
};Flatness — . 3 , ( ). — Another, . ( — if — .)
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two);
};Class .
class ConvexHull
{
struct Flatness;
struct Edge;
std::vector<Point> points_; //
std::vector<Flatness> verge_; //
std::vector<Edge> edges_; //
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull(); }
};
: Z ( , )
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}, :
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}. (-)
. , : . - , , .
:
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point; //
first_point = findMinZ();, Z. "".
double min_angle = 7; // 2pi, 7
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i) //
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;, .
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;, , XY, (0, 0, 1). .
( ), .
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
} :
:
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);: , . , : .
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}, , e , . , , is_closed = true, , , , — — , .
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id); // -1,
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} // #include <iostream>
#include <vector>
#include <cmath>
#include <stack>
#include <iomanip>
using coordinate = int64_t;
struct Point;
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22);
Point VectorProduct(const Point& A, const Point& B, const Point& C);
double GetLenghtVector(Point A, Point B);
double GetAngle(const Point& n1, const Point& n2);
struct Point
{
coordinate x;
coordinate y;
coordinate z;
Point(coordinate x = 0, coordinate y = 0, coordinate z = 0) : x(x), y(y), z(z) {}
Point operator-(const Point& other) const
{
return Point(x - other.x, y - other.y, z - other.z);
}
Point operator+(const Point& other) const
{
return Point(x + other.x, y + other.y, z + other.z);
}
bool operator!= (const Point& other) const
{
return (x != other.x || y != other.y || z != other.z);
}
bool operator== (const Point& other) const
{
return (x == other.x && y == other.y && z == other.z);
}
};
coordinate Det2x2(coordinate a11, coordinate a12, coordinate a21, coordinate a22)
{
return a11 * a22 - a12 * a21;
}
//[AB, AC]
Point VectorProduct(const Point& A, const Point& B, const Point& C)
{
Point a = B - A;
Point b = C - A;
return Point (Det2x2(a.y, a.z, b.y, b.z),
Det2x2(a.x, a.z, b.x, b.z),
Det2x2(a.x, a.y, b.x, b.y));
}
//vector AB
double GetLenghtVector(Point A, Point B = Point(0, 0, 0))
{
Point vec = B - A;
double lenght = std::sqrt(vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
return lenght;
}
double GetAngle(const Point& n1, const Point& n2)
{
double len_n1 = GetLenghtVector(n1);
double len_n2 = GetLenghtVector(n2);
double scalar_prod = n1.x * n2.x + n1.y * n2.y + n1.z * n2.z;
if (scalar_prod == 0)
{
return 0;
}
return std::acos((scalar_prod) / (len_n1 * len_n2));
}
class ConvexHull
{
struct Flatness
{
int first;
int second;
int third;
Point normal; // ,
Flatness(int first, int second, int third, Point normal) :
first(first), second(second), third(third), normal(normal) {}
int Another(int one, int two)
{
if ((one == first && two == second) || (one == second && two == first))
{
return third;
}
if ((one == first && two == third) || (one == third && two == first))
{
return second;
}
if ((one == third && two == second) || (one == second && two == third))
{
return first;
}
return -1; // error
}
};
struct Edge
{
int first;
int second;
int flatness; //
bool is_close = false;
Edge(int first, int second, int flatness = -1, Point normal = Point(0, 0 , 0)):
first(first), second(second), flatness(flatness) {}
};
std::vector<Point> points_;
std::vector<Flatness> verge_;
std::vector<Edge> edges_;
int count_; //
int findMinZ() const;
void findFirstFlatness();
int returnIsEdgeInHull(int a, int b) const;
void makeHull();
public:
ConvexHull(const std::vector<Point>& points): points_(points), count_(points.size()) { makeHull();}
};
void ConvexHull::makeHull()
{
findFirstFlatness();
std::stack<int> stack;
stack.push(0);
stack.push(1);
stack.push(2);
while (!stack.empty())
{
Point new_normal;
Edge e = edges_[stack.top()]; // ,
stack.pop();
if (e.is_close) // ,
{
continue;
}
int min_id = -1;
double min_angle = 7;
for (int i = 0; i < count_; ++i)
{
int another = verge_[e.flatness].Another(e.first, e.second);
if (i != another && e.first != i && e.second != i) // ,
{
// , i-
Point current_normal = VectorProduct(points_[e.second], points_[e.first], points_[i]);
double angle = GetAngle(current_normal, verge_[e.flatness].normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
new_normal = current_normal;
}
}
}
if (min_id != -1) // - 4
{
e.is_close = true; // ,
int count_flatness = verge_.size(); //
int first_edge_in_hull = returnIsEdgeInHull(e.first, min_id);
int second_edge_in_hull = returnIsEdgeInHull(e.second, min_id);
if (first_edge_in_hull == -1)
{
edges_.push_back(Edge(e.first, min_id, count_flatness));
stack.push(edges_.size() - 1);
}
if (second_edge_in_hull == -1)
{
edges_.push_back(Edge(min_id, e.second, count_flatness));
stack.push(edges_.size() - 1);
}
if (first_edge_in_hull != -1)
{
edges_[first_edge_in_hull].is_close = true;
}
if (second_edge_in_hull != -1)
{
edges_[second_edge_in_hull].is_close = true;
}
verge_.push_back(Flatness(e.first, e.second, min_id, new_normal));
}
} // while
} //
int ConvexHull::findMinZ() const
{
int min_id = 0;
for (int i = 1; i < count_; ++i)
{
if (points_[i].z < points_[min_id].z ||
(points_[i].z == points_[min_id].z && points_[i].y < points_[min_id].y) ||
(points_[i].z == points_[min_id].z && points_[i].y == points_[min_id].y &&
points_[i].x < points_[min_id].x))
{
min_id = i;
}
}
return min_id;
}
void ConvexHull::findFirstFlatness()
{
int first_point, second_point, third_point;
first_point = findMinZ();
double min_angle = 7;
int min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i)
{
continue;
}
Point start = points_[first_point];
Point next = points_[i];
double angle = GetAngle(start - next, next - Point(next.x, next.y, start.z));
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
second_point = min_id;
min_angle = 7;
min_id = -1;
for (int i = 0; i < count_; ++i)
{
if (first_point == i || second_point == i)
{
continue;
}
Point normal = VectorProduct(points_[first_point], points_[second_point], points_[i]);
double angle = GetAngle(Point(0, 0, 1), normal);
if (min_angle > angle)
{
min_angle = angle;
min_id = i;
}
}
third_point = min_id;
//
if (VectorProduct(points_[first_point], points_[second_point], points_[third_point]).z > 0)
{
std::swap (second_point, third_point);
}
Point new_normal = VectorProduct(points_[first_point], points_[second_point], points_[third_point]);
verge_.push_back(Flatness(first_point, second_point, third_point, new_normal)); //
edges_.push_back(Edge(first_point, second_point, 0));
edges_.push_back(Edge(second_point, third_point, 0));
edges_.push_back(Edge(third_point, first_point, 0));
}
int ConvexHull::returnIsEdgeInHull(int a, int b) const
{
for (int i = 0; i < edges_.size(); ++i)
{
if ((edges_[i].first == a && edges_[i].second == b) ||
(edges_[i].first == b && edges_[i].second == a))
{
return i;
}
}
return -1;
}.