👩🏿‍✈️ 🧑🏿 🏨 密码学中的背包问题 ▫️ 🛀 👦🏼

密码学中的背包问题（Knapsack问题）是美国密码学家Ralph Merkle和Martin Hellman在其基础上开发的第一个公共密钥加密算法的问题。

在程序中进一步

提出背包问题（+为什么要提背包？）
轻松而艰巨的挑战
示例
历史

什么是公钥加密？

, , «», .

. , , , .

: , .

, - !

第一个通用公钥算法使用背包算法。

根据公共密钥系统的定义，需要两个密钥才能成功加密（和解密）消息。消息的“合法”收件人知道密钥

А

而发件人拥有另一个公钥

B

$B$ ...

如果公钥被攻击者知道该怎么办？

有一个答案：必须使用转换（单向函数）从私钥中获取公钥。

f

$f$ 具有以下两个属性：

$B = f(A)$ 知道A，就很容易计算函数本身

$A = f^{-1} (B)$ ，并且很难计算逆函数

什么是“容易”和“困难”？

.

«» , . ..

n

$n$ , —

t \propto n^{a}

$t \propto n^a$ ,

a

$a$ — . , .

«» . , , .

..

n

$n$ ,

t \propto 2 n

$t \propto 2n$ , , .

背包问题的公式如下

集合（背包向量）

A = (a_{1}, . . ., a_{n})

$A = (a_1, ... , a_n)$ 是有序的

n

$n$ （

n > 2),

$n > 2),$ 不同的自然数

a_{i}

$a_i$ ... 让有一个数字

k

$k$ -整体而积极。任务是找到这样的一套

a_{i}

$a_i$ 这样总的来说

k

$k$ ...

在背包问题的最著名版本中，需要找出给定的一对是否具有

(A, k)

$(A , k)$ 决定。在密码学中使用的变体中，您需要此输入

(A, k)

$(A , k)$ 在知道存在这样的解决方案的情况下构建解决方案。这两个选项都是NP完整的。

背包类比

在最简单的情况下

k

$k$ 表示背包的尺寸（容量），每个数字

a_{i}

$a_i$ 表示可以装进背包的物品的尺寸（重量）。我们的任务是找到这样一组物品，以便

背包完全装满。

即，假设您有一组砝码1、6、8、15和24，则需要打包一个30磅的背包。

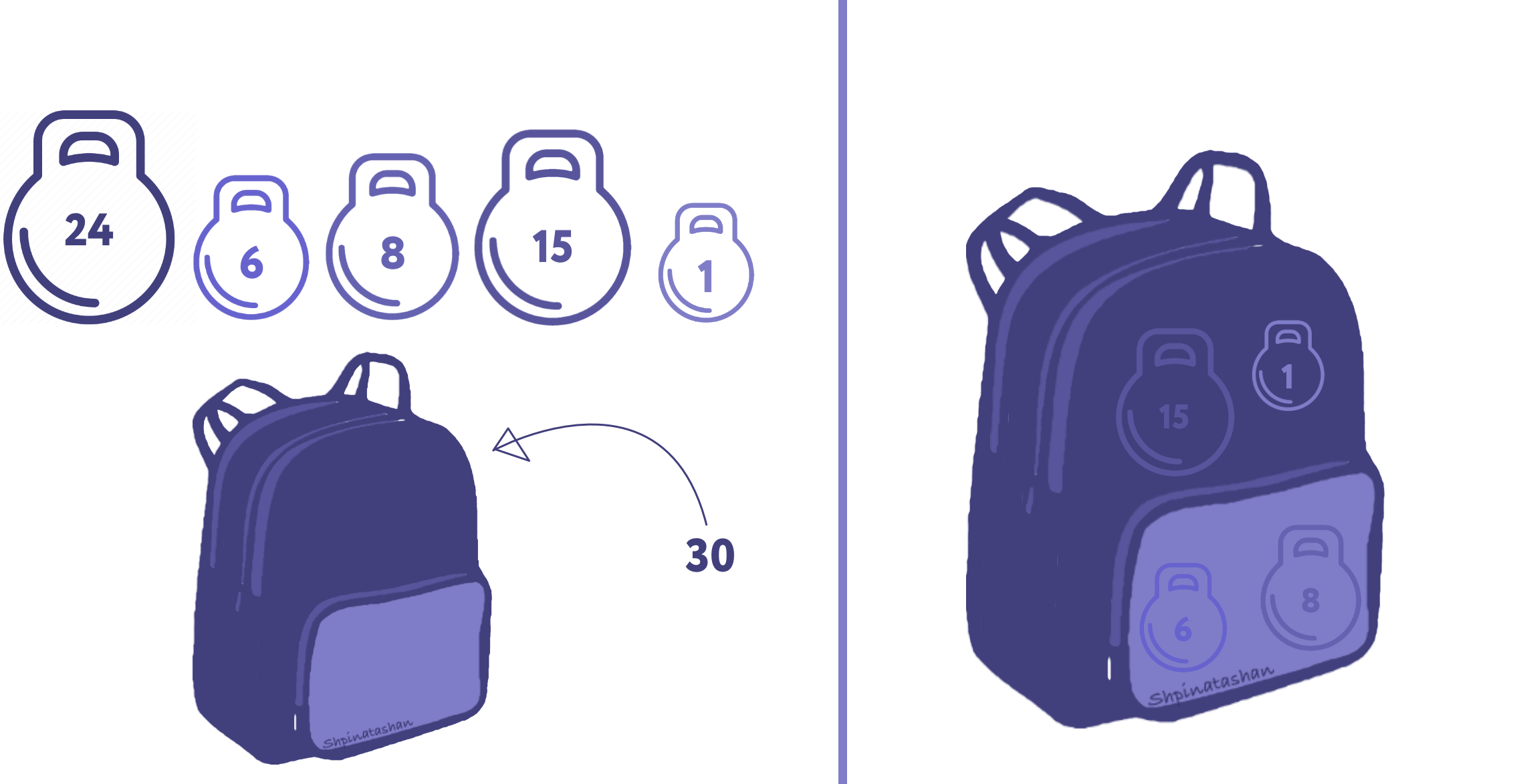
原则上，总可以通过彻底搜索子集找到解决方案

А

并检查他们的总和是

k

$k$ ... 在我们的情况下，这意味着蛮力

2^{5} = 32

$2^5 = 32$ 子集（包括空集）。这是完全可行的。

但是如果有几百个数字怎么办 $a_i$ ？

在我们的示例中，n = 5，以便不使表示复杂化。在实际条件下，一个示例将有300个

a_{i} - х

$a_i-$ ... 最重要的是，与穷举搜索相比，算法的复杂度要低得多。在其中搜索

2^{300}

$2^{300}$ 子集无法处理。事实上，背包问题被称为NP完全... NP完全问题被认为是难以计算。

该功能是否满足指定要求？

我们定义功能

f (x)

$f(x)$ 以以下方式。任何数字

0 \leq x \leq 2 n - 1

$0 ≤ x ≤ 2n − 1$ 可以由

n

$n$ 位，如有必要，在其中添加前导零。现在让我们定义

f (x)

$f(x)$ 作为从

A

$A$ 总结所有这些

a_{i}

$a_i$ 二进制表示法中的相应位

x

$x$ 等于1。

即，

f (1) = f (0 . . . 001) = a_{n}

$f(1) = f(0 . . . 001) = a_n$

f (2) = f (0 . . . 010) = a_{n - 1}

$f(2) = f(0 . . . 010) = a_{n−1}$

f (3) = f (0 . . . 011) = a_{n - 1} + a_{n}

$f(3) = f(0 . . . 011) = a_{n−1} + a_n$

. . .

$...$

功能

f (х)

$f( )$ 确定

n -

$n-$ 组

A

$A$ ... 显然，如果我们能够计算

x

$x$ 的

f (x)

$f(x)$ ，那么几乎可以同时解决背包问题：

x

$x$ 它的二进制表示立即被计算，从而给出集合的成分

A

$A$ 包括在

f (x)

$f(x)$ ... 另一方面，计算

f (x)

$f(x)$ 的

x

$x$ 轻巧。由于背包问题是NP完全的，

f (x)

$f(x)$ 是单向功能的理想人选。当然，必须要求 $n$ 足够大，少不了 $200$ ...

加密

纯文本

(. plain text) — , , . ( ).

有两种加密方法：

通过将背包向量的元素提高到加密消息的相应位的幂，然后将所有结果相乘，即可得到消息密码。 $A = (2,3,5)$ 和消息 $(100)$ ，则密码将是数字 $2^1*3^0*5^0=2$ ... 这是乘法的方式。
通过将此背包向量的元素乘以加密消息的相应位，然后将所有结果相加，即 $A = (2,3,5)$ 和消息 $(100)$ ，则密码将是数字 $2^ *1+3^ *0+5^ *0= 2$ ... 此方法称为加法。

示例

要以二进制表示形式对纯文本进行加密，则将其分成多个长度的块

n

$n$ （例如，您可以用二进制11110表示权重30）。据信，一个表示背包中有物品，而零表示它不存在。

背包加密为创建公共和私有密钥提供了一种很好的方法，其中私有密钥易于使用，而公共密钥难以确定。

因此，我们可以创建一个系统，其中：“硬”问题将用作

公钥；有了它，您可以轻松加密，并且无法解密消息。

私钥-“简单”问题将作为使用它，您可以轻松地解密邮件。如果没有私钥，则必须解决“困难”的背包问题。

“容易”的问题

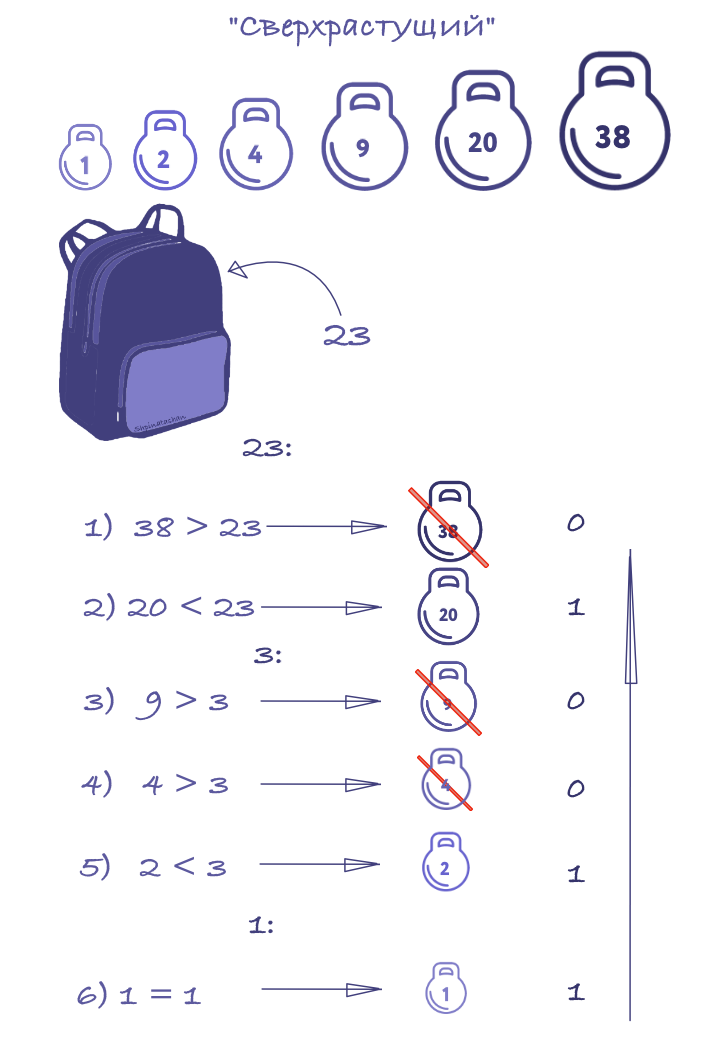
超级成长背包矢量

A = (a_{1}, . . ., a_{n})

$A=(a_{1},...,a_{n})$ ,

Σ_{i = 1}^{j - 1} a_{i} < a_{j}

$Σ_{i=1}^{j-1} a_{i} < a_{j}$

j = 2, . . ., n

$j=2,...,n$ , . .

对于超增长向量A，背包问题很容易解决。那些。背包很容易组装。

让我们举个例子：

算法

.

, , . , .
.
(1)-(2) .

, .

“难题

解密非超大背包的问题要困难得多。

Merkle和Hellman创建了一种算法，该算法使用超大号私钥背包和非超大号公钥背包。

他们通过承担超大背包任务并将其转换为非超大任务来完成此任务。

（Merkle和Hellman使用模块化算法，设计了一种将“轻”背包变成“硬”背包的方法）

创建公用密钥

几个重要概念

$(x, mod m)$ $x$ $m$ ,

$x$ — , $m > 1$ , [x/m] — ,
$x = (x, m o d m) + [x / m] * m$
$x = (x, mod m) + [x/m]*m$

$A$ , $m > max A$ $t < m$ , $(t, m) = 1$ .

$B = (b_1, . . . , b_n)$ , $b_i = (ta_i, modm)$ , $i = 1, . . . , n$ , , B A m t , , $(m, t)$ .

$(t, m) = 1$

$t^{−1} = u$ , ,

$t u \equiv 1 (m o d m)$
$tu ≡ 1 (mod m)$

$1 ≤ u < m$ . , $A$ $B$

$m, u$ .

$m > max A$

$m > Σ_{i=1}^{n} a_{i}$ , , $B$ $A$ $m, t$ .

— , , , .

密码系统的创建者选择了这样的系统

A, t, m, B

$A, t, m, B$ 该向量

A

$A$ 超级增长

B

$B$ 来自

A

$A$ 相对于

m, t

$m, t$ ... 向量

B

$B$ 扩展为加密密钥和长度为二进制的块

n

$n$ 以数字形式发送给设计师

β

$β$ 使用向量获得

B

$B$ ...

邮件拦截器必须解决背包问题才能进入

(B, β)

$(B, β)$ ... 密码系统的创建者计算

α = (u β, m o d m)

$α = (uβ, modm)$

并解决背包进入问题

(A, α)

$(A, α)$ ...

以下引理说明了为什么所有这些方法都有效。

引理。让我们假装

A = (a_{1}, . . ., a_{n})

$A = (a_1, . . . , a_n)$ 超级成长矢量图和矢量

B

$B$ 衍生自

A

$A$ 相对于

m, t

$m, t$ ... 进一步假设

u \equiv t^{- 1} (m o d m)

$u ≡ t^{−1} (mod m)$ ，

β

$β$ -任意自然数和

α = (u β, m o d m)

$α = (uβ,modm)$ ... 那么以下陈述是正确的。

（i）背包问题

(A, α)

$(A, α)$ 可在线性时间内解决。如果存在解决方案，那么它是唯一的。

（ii）背包问题

(B, β)

$(B, β)$ 最多有一个解决方案。

（iii）如果有解决方案，请输入

(B, β)

$(B, β)$ 那么它匹配唯一的入口解决方案

(A, α)

$(A, α)$ ...

证明（第104页）

示例

考虑一个超增长序列；该序列不存在。例如{1、2、4、10、20、40}。模数必须大于序列中所有数字的总和，例如110。乘数不应与模数有共同的因数。因此，让我们选择31。

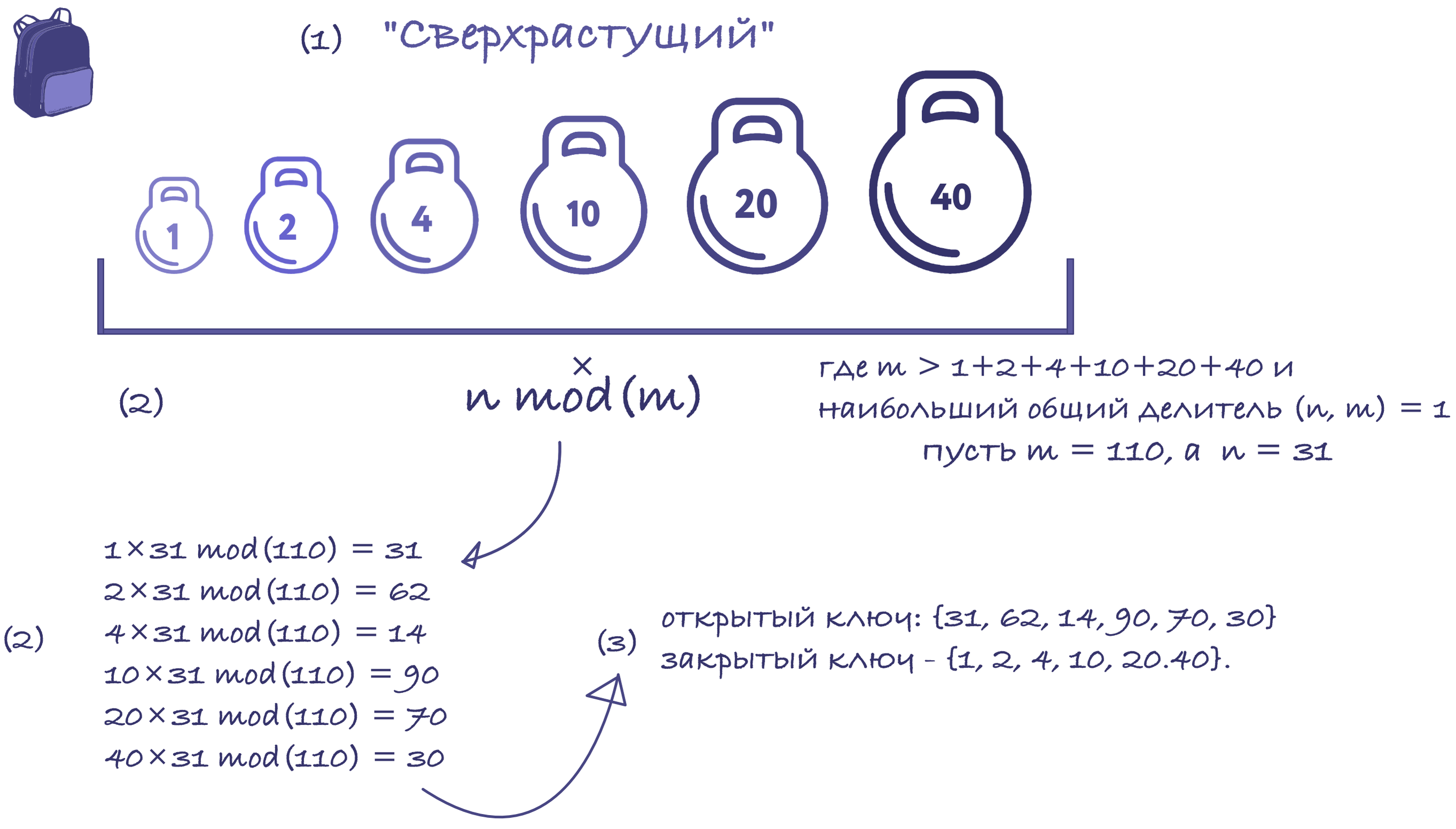
因此，我们计算了公钥：{31、62、14、90、70、30}和私钥– {1、2、4、10、20.40}。

现在让我们尝试发送一个二进制序列：100100111100101110

公钥的一些好处

当使用公共密钥密码系统时，双方不见面，他们甚至可能彼此不认识并且使用任何形式的通信。

密钥长度。在对称密码学中，如果密钥长于原始消息，则不会获得真正的收益。对于公共密钥密码系统，加密密钥的长度无关紧要，因为它是公共的和公共的。因此，解密密钥的长度不是很重要（接收者仅将其存储在秘密的地方）

历史

长期以来，背包式密码系统由于其NP完整性和高速的加密和解密而被认为是最有吸引力和最有前途的密码系统。许多方案都使用背包问题（有各种变体），以下只是其中的几种：紧凑背包问题，乘法背包问题，模块化背包问题，矩阵覆盖问题，群分解问题……

不幸的是，大多数方案都容易受到影响攻击。事实证明，尽管这个问题被称为NP完全问题，但基于背包问题设计安全的密码系统并非易事。大多数背包密码系统已被黑客入侵。尽管如此，与整数分解和离散对数相反，一般背包问题（解决方案）是一个经过证明的NP完全问题。

有人认为有一天可以发明多项式时间算法来解决整数分解和离散对数问题，而背包问题仍然是NP完全的。

这里有几个“ BUT”。

首先，NP完整性基于最坏情况分析，其次，NP完整性是普遍问题的特征，而不是特定情况。这意味着，如果考虑平均复杂度，则背包问题可能很简单。

该材料是根据以下文献制备的：

（1） A. Salomaa。公钥密码术。 -斯普林格出版社（1990）。 75-82，第101-111页

（2）闵健来背包加密系统：过去和未来-加利福尼亚大学，2001年

（3）王保苍，吴谦宏，胡玉璞。基于背包的概率加密方案。2007

（4） - （5）

密码学中的背包问题

背包问题的公式如下

背包类比

加密

“容易”的问题

“难题

公钥的一些好处

历史

More articles: