 如果类似于两次狭缝实验,粒子到屏幕的路径上的所有空间都充满了缝隙,将会发生什么?
如果类似于两次狭缝实验,粒子到屏幕的路径上的所有空间都充满了缝隙,将会发生什么?
« — , .»
« » —
C:
- :
- ,
:
在19世纪初,决定论在世界的科学图景中占主导地位-这种理论认为系统的初始参数完全决定了系统的进一步发展。牛顿力学使人们可以非常准确地预测不太大的物体以比光速低得多的速度运动的行为,后来出现的特殊和通用的相对论使得对于非常大的物体以接近光速的速度运动也可以进行类似的计算。
拉普拉斯恶魔的出现似乎只是一种假设的计算设备,它能够接收任何系统的初始参数作为输入并随时计算其站立时间,只是时间问题。尽管拉普拉斯恶魔存在的可能性与之相关的自相矛盾已经引起了极大的怀疑,但科学家们已经开始预见到将几乎完全战胜不确定性和人类思想的胜利。

但是几乎同时,研究人员试图以极小的时空尺度穿透自然结构给确定性带来了坏消息。因此,新量子理论的主要陈述之一是不确定性原理,它说,如果系统已连接(交换)参数,则我们测量其中一个参数的精度越高,确定另一个参数的确定性就越差。
基于这些想法,无法准确预测任何事件,因为任何测量都存在一定的不确定性,而且这一事实并不符合当时科学界的许多成员的喜好。批评者的阵营是由爱因斯坦,那个时候谁已经有世界权威,谁当家对应 与他的对手和同事海森堡-麦克斯·伯恩(Max Born)谈到不确定性原则的可能性:“无论如何,我相信[上帝]不会掷骰子。”

不确定性原理,纹身和书法
不确定性原理的操作通常归因于测量过程本身的属性,但是还有更多的根本原因,最简单的方法是通过两个参数来举例说明它们:动量和粒子坐标。就像可以以两种根本不同的方式完成同一幅图一样:矢量和光栅,即以线的形式(例如在书法中)或以点集的形式(例如在纹身中)。同样,可以通过两种替代方式描述粒子的运动:借助动量-质点速度矢量 或使用一组时空坐标

左:书法大师绘制恩索符号(円相,),来源。右:纹身人体皮肤的过程,来源。
根据不确定性原理,我们将更准确地确定时空中物体的坐标
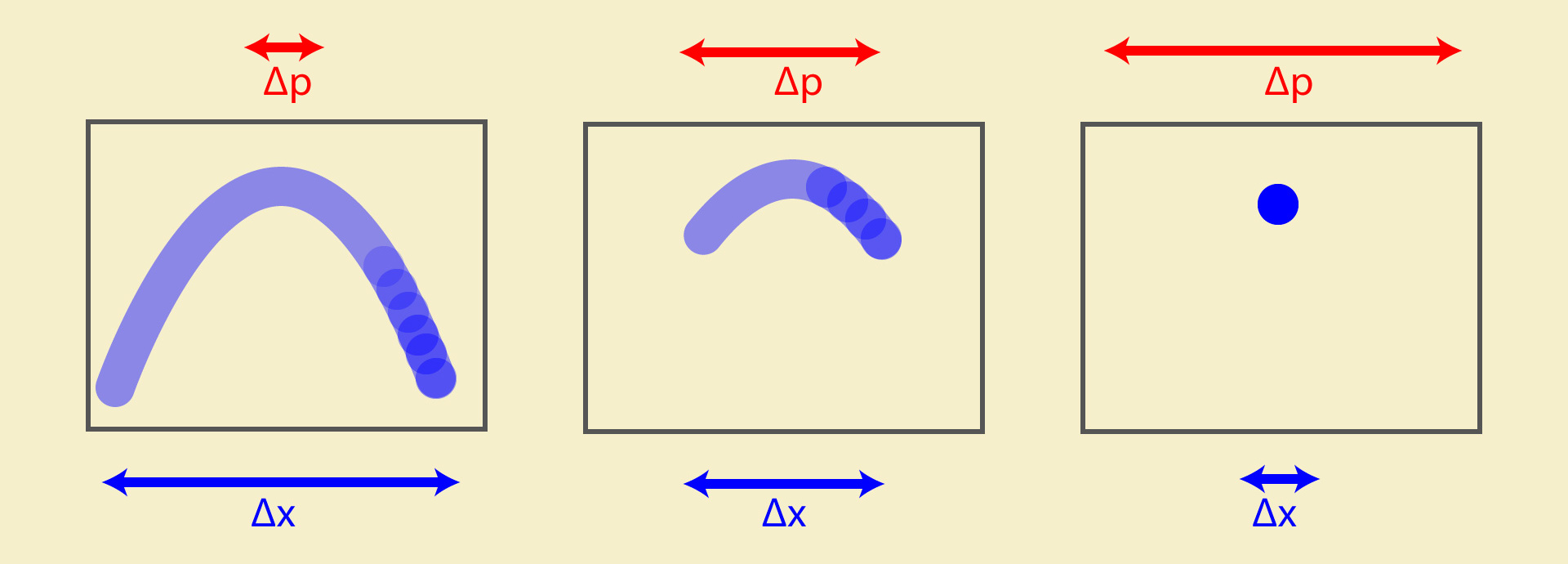
从左到右分别显示了三个运动对象的镜头,随着时空间隔(相机快门速度)的增加,有关脉冲的信息量(粒子轨迹)如何减少。
在宏观物体的世界中,这种影响不是大问题,如果我们要以与汽车本身大小相当的精度来设置汽车的坐标,那么就不会有问题-汽车可以安全地进入隧道并仍保持其可预测的轨迹。但是,如果我们尝试对光子执行相同的操作,并开始通过逐渐减小的缝隙传输它们,那么起初,光点将如预期的那样变得越来越窄,但是当缝隙的大小与光子波长可比时,缝隙出口处的光子轨迹将变为越来越难以预测,并且光斑将开始在宽度上扩展。换句话说,我们越准确地知道粒子从何处飞过,对粒子下一步将移动到哪里的了解就越少。

以上,从左至右:用连续狭缝还原,得到的干涉图案源。底部:实验装置图,来源。
物质波及其振幅
但是很难让人受到光线的干扰,因为每个人都已经知道光是波,并且波前的每个点也将成为波的来源,并且通过减小间隙,根据惠更斯-菲涅耳原理,我们得到了第二个前锋,而第二个前锋缝隙的大小将越来越像来自点源的波浪。
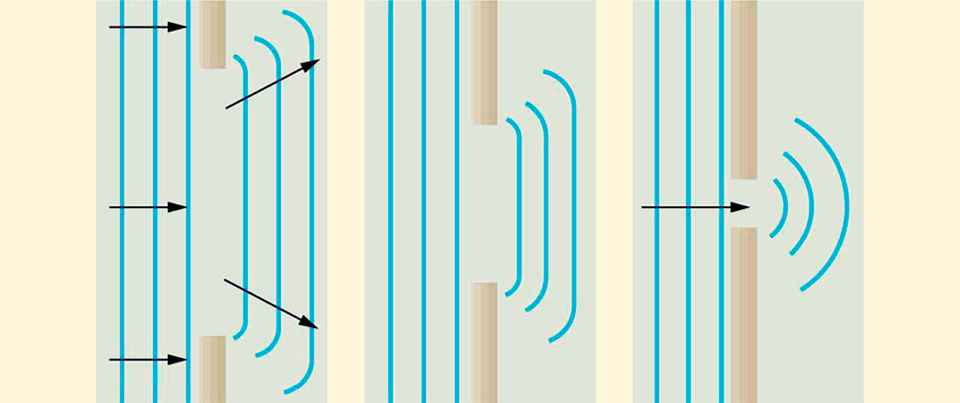
穿过孔,源的正向波阵面的衍射。
实际上,由于其几何性质,任何波都不会局限在一个点上,因为要生成最简单的波,就需要进行两次测量-波幅(高度)和波长(宽度)。如果我们开始压缩波浪的高度,那么它将在长度上扩展,反之亦然。但更有趣的是,对物质粒子(电子,原子甚至有机分子)进行了类似的实验,并且它们都展示了波衍射。
1923年,法国物理学家路易斯·德布罗意(Louis de Broglie)在他的著作《波浪与量子》中首次提出了不仅光子而且总的说来任何东西都具有波性质的想法。”这一假说是部分已经在1927年确认,作为戴维森-革末实验,这表明电子的波衍射,这带来了德布罗意当之无愧诺贝尔物理学奖于1929年的结果
后来,公知的双缝实验用电子,输送这表明物质粒子的波不仅可以经历弥散,形成次级波阵面,而且这些次级波还可以彼此放大,以相同的相位相遇,或者相反地相互熄灭,以反相相遇,形成干涉图案,类似于宏观水波或声波。

: , . : , , .
但是,如果在水中的波浪-水粒子上下的这种振荡运动,声波-类似于空气分子的运动,振荡其是波的物质,其可以是一个光子,原子,分子,人?正式地,科学家们从未对此分数达成共识,但是,他们学会了根据坐标或可以测量的任何其他参数来计算描述该波的函数,并发现该函数模数的平方是概率的准确估计。测量结果。因此,包括杰出物理学家理查德·费曼(Richard Feynman)在内的许多科学家将其称为波函数-具有概率振幅。所有的物质和辐射都是某些抽象的数学概念的波,这似乎有些奇怪,但是正如我们将试图进一步说明的那样,通过接受该陈述,您可以对许多量子效应获得相当清晰的解释。
复数和概率阶段
从一个和两个狭缝的实验中我们已经知道,在许多方面,概率振幅的行为都像最普通的波一样,甚至可以通过双狭缝,彼此重叠,增加或反之减少粒子出现在某个点上的可能性,从而产生干涉图案。

. : — . : . .
并且,如果我们将事件的概率定义为导致事件的结果数与所有可能结果的总数之比,则可以得出该概率是一个正数,介于零到一之间,但是如果我们采用任意两个密度图在某个点找到粒子的概率,我们将看到这些图的振幅相加总会大于分别大于每个图的振幅,并且不会获得破坏性干扰。
如果我们将属性添加到使它们发生干扰的概率波中怎么办?想象一条直线,其上的每个点都将对应于粒子的坐标,然后从每个点垂直地推迟与该点处的粒子位置相对应的概率。连接点
您可能已经猜到,这种结构与复数非常相似,复数也具有模数-长度和相位-角度。然后,每个坐标将对应一个复杂的平面,其中概率矢量将像钟针一样旋转,如果它们朝一个方向看,它们将加起来,如果朝相反的方向,它们将被减去。通过连接这些箭头的两端,我们得到了波动函数的形状或粒子沿一维直线移动的概率的幅度。
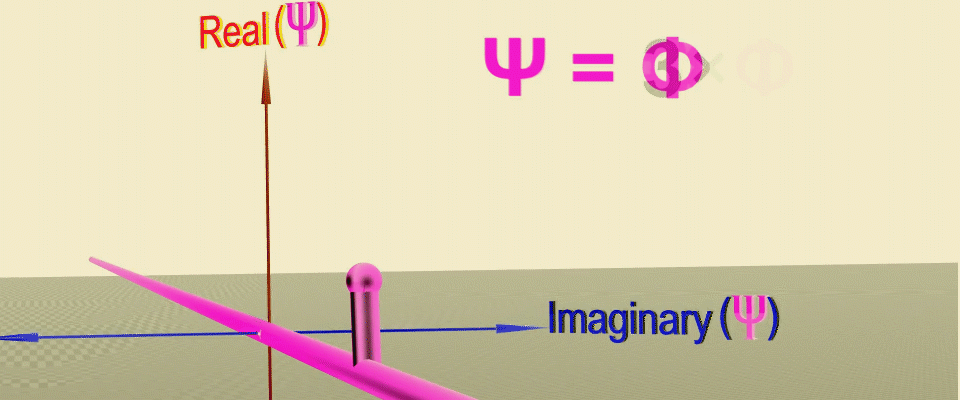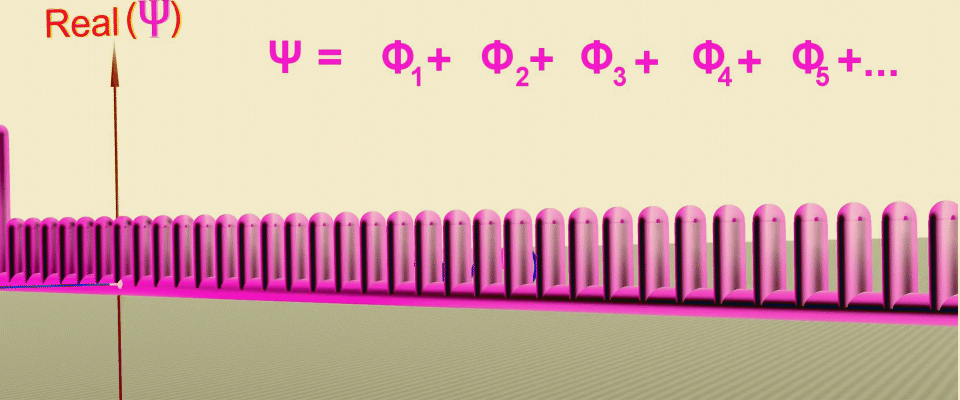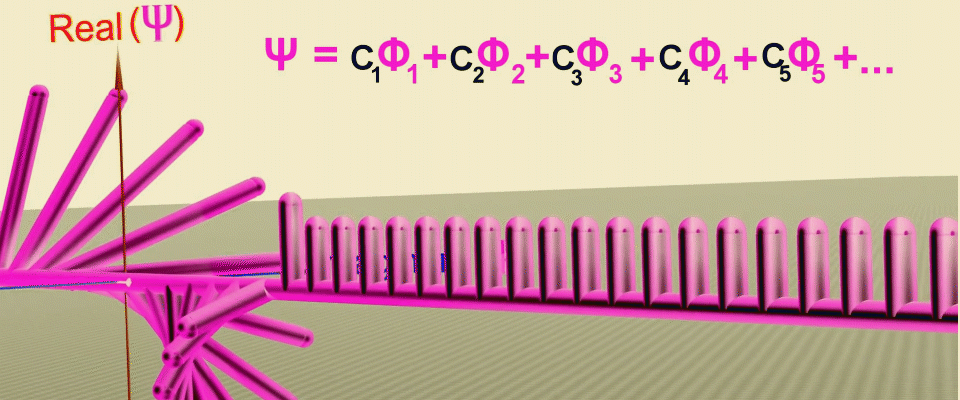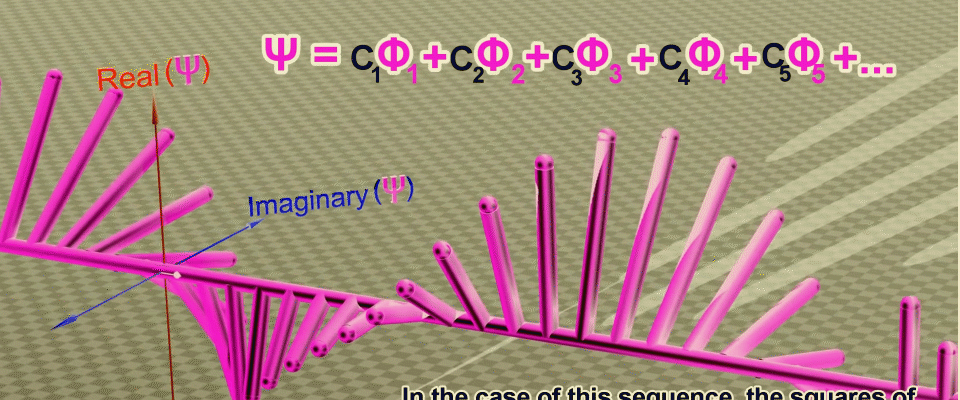
连续变换的动画,可以让您获得波函数作为沿粒子路径(绿线)上的点处的概率振幅之和,首先设置振幅的实部,然后设置复数平面中的相位(旋转角度)。来源。
复数的形式为
量子理论的基本公理之一被称为伯恩定律(Born Rule),它指出,波动函数模的平方为我们提供了概率密度函数,即在我们的示例中,根据坐标找到粒子的概率分布。
快速刷新内存,复数的模数是到原点的距离-
( x 2 + ( y − 1 ) 2 ) 2 = x 2 + ( y − 1 ) 2 = ( x + y − 1 ) ( x − y − 1 )
我们得到一个复数模量的平方是其乘以相同复数的乘积,仅在虚部系数之前的符号不同
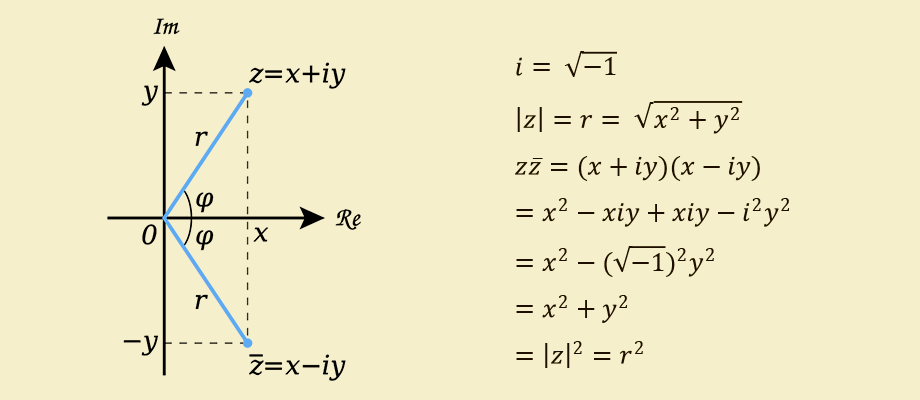
哪里:-复共轭数 z ¯
虚构单位的真实世界
这是我们已经理解的:wave函数为每个坐标分配一个特定的复数。实际上,这就是波动函数的作用-它们将复数分配给一些可测量的参数,该参数的旋转角度称为相位。复数相位负责放大和衰减概率的干扰效应,这是通过将波函数乘以其镜面反射-复共轭来获得的。
当被问及为什么波函数模的平方会给出概率密度时,量子理论通常会回答-
让我们想象一下,我们对波函数或概率密度函数一无所知,只是简单地进行了许多观察并用点标记了粒子出现的位置和频率。同时,我们了解到,必须用某种概率密度函数图来描述结果的分布,知道该函数本身将非常有用。
为了找出哪个函数与我们的点相对应,让我们以最简单的方式开始对数据进行拟合,即选择将通过最大可用点数的多项式。让我们从两个点开始,为它们选择第一阶多项式的系数,即线性函数

使用numpy.polyfit函数从具有正态分布的正态分布的概率密度函数中提取的拟合点示例,该多项式的阶数从线性到18次。您可以确保多项式的阶数对应于其图形通过的点数。
Python代码:from numpy import * from matplotlib.pyplot import * from mpl_toolkits.axes_grid.axislines import SubplotZero mu, sigma = 0, 0.1 x = np.arange(-1,1,0.02) y = 1/(sigma * np.sqrt(2 * np.pi))*np.exp( - (x - mu)**2 / (2 * sigma**2) ) y1 = poly1d(polyfit(x,y,1)) # linear y2 = poly1d(polyfit(x,y,2)) # quadratic y3 = poly1d(polyfit(x,y,3)) # cubic y4 = poly1d(polyfit(x,y,4)) # 4th degree y5 = poly1d(polyfit(x,y,10)) # 10th degree y6 = poly1d(polyfit(x,y,18)) # 18th degree fig = figure(figsize=(20,8), facecolor='#f4efcb', edgecolor='#f4efcb') ax = SubplotZero(fig,111) fig.add_subplot(ax) ax.plot(x,y1(x),'r',label=u'') ax.plot(x,y2(x),'g',label=u'') ax.plot(x,y3(x),'orange',label=u'') ax.plot(x,y4(x),'b',label=u'$4$ ') ax.plot(x,y5(x),'c',label=u'$10$ ') ax.plot(x,y6(x),'m',label=u'$18$ ') ax.plot(x,y,'k.',label=u'') ax.set_xlabel(u'x') ax.set_ylabel(u'y') ax.set_facecolor('#f4efcb') ax.minorticks_on() ax.legend(frameon=False,loc=8,labelspacing=.2) ax.annotate(' 18 :'+'\n'+str(y6.coeffs), xy = (-1,1.2)) setp(ax.get_legend().get_texts(), fontsize='large') fig.savefig("Curve fitting.svg",bbox_inches="tight",pad_inches=.15)
并且由于概率密度可以通过多项式近似,因此该多项式肯定有根,并且还有一个奇妙的定理,代数的主定理说是的,任何多项式都必须具有复数解,并且如果根是实数,那么这意味着虚部等于零(向量的旋转角为零),因为实数集完全包含在复数集中
如果有复数
例如,让我们想象一下,概率密度是由二阶多项式描述的
另一方面,知道了根并使用Vieta的公式,我们可以如下分解相同的平方三项式:
当然,这是一个非常宽松的推理,旨在以某种方式理解正在发生的事情,并通过一个简单的示例显示复数是完全有理的,并且其共轭乘积可以提供类似于概率密度的信息。

漫画带笑话,涉及实数和波函数乘以其自身的复杂共轭。来源
好的,让我们假设我们对概率振幅如何工作,为什么它们很复杂以及如何从中得出普通概率有一些想法。我们可以继续讨论这些概率为我们预测的问题,即有关测量结果的问题。
波动函数和概率密度
通过获得在某个坐标中找到粒子的概率密度,我们可以预测在不同点观察粒子的频率。例如,如果概率密度由高斯曲线描述(如下图左侧所示),则
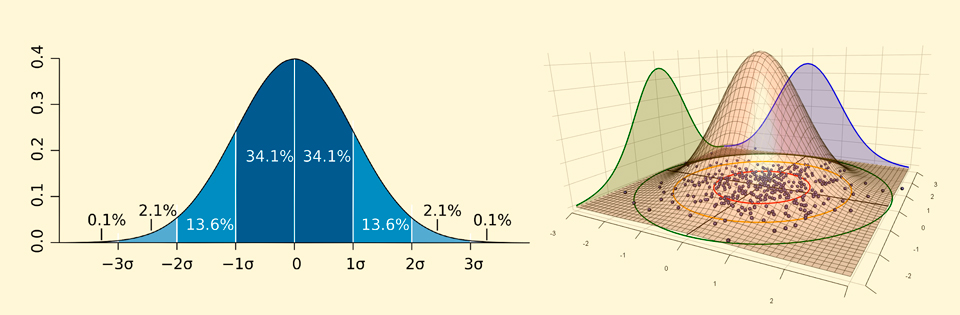
一个相当简单的方案:坐标的波动函数设置分布的形状,然后告诉我们在空间点测量粒子的可能性。但是,这种解释会导致奇怪的矛盾,有时将粒子视为概率振幅的波更为自然。例如,下面的左图显示了电子与氢核相互作用的概率密度。根据该图,您可以得到所谓的电子轨道的形状-原子核周围最可能与电子发生相互作用的区域,如右图所示:

左:在三个能级上在单个质子附近找到电子的概率密度曲线
在上图中,您可以看到轨道的形状如何根据电子的能级而变化-电子的能量越高,首先,壳的半径越大,这是可以理解的,因为能量越大,电子越能抵抗核的吸引力,并且越强从原子核可以相互作用,但同时,每个新的能级都添加了一个概率为零的部分,称为节点,因此,例如,电子在第三能级的轨道具有层状球体的形式,其内部包含两个区域,即概率检测零电子。
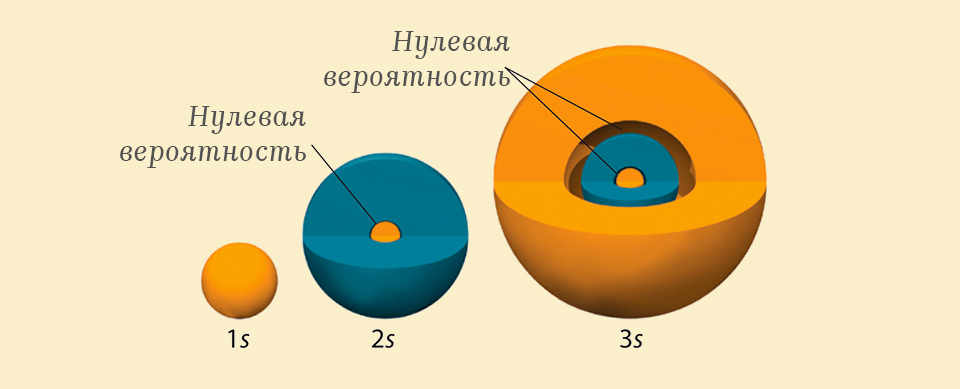
在从左到右的三个能级上,在一个氢原子核附近发现电子的概率轮廓:1s,2,s 3s。来源。
这样的概率分布看起来很奇怪,因为从一个球体到另一个球体如果不跨越它们之间的嵌套球体是不可能的。
但是,如果您将电子视为概率的振幅,那么一切都会很自然地得到解释,在下图中是氢原子周围电子半径的波动函数,在一维中针对三个能级计算。

查看波函数的图形,可以更容易地理解,原子核所持有的电子是驻波,并且像任何驻波一样,它将具有所谓的节点(节点)-由于对反射波的干扰而导致振幅为零的区域。
 一维驻波源中干扰节点(红点)的形成示例。
一维驻波源中干扰节点(红点)的形成示例。
如果一维波(如上图中的动画)仍然不像氢原子的分层三维电子壳的形状,那么我建议想象一个在二维平面上从点源传播的波。因此,要查看此类二维波的完整形状,您需要将其分为三个部分测量。对于一个二维世界的居民来说,这样的波浪只会是一组偏离中心的圆。同样,在三维波中,它们生活在四个维度中,但对我们来说,它们看起来就像是发散的三维球体。

右:在2D表面上传播的波的动画。左:该波在平面上的投影示例。
量子退相干势垒
亚伯拉罕·佩斯(Abraham Pais)是一位杰出的物理学家和科学史学家,与20世纪科学传奇星系合作,其中包括:约翰·冯·诺依曼,艾伯特·爱因斯坦,尼尔斯·玻尔,麦克斯·伯恩,保罗·狄拉克,沃尔夫冈·保利等。在描述有关量子物理学中观察者问题的对话之一时,他引用了爱因斯坦向他提出的一个问题:
“你真的认为月亮只有在你看时才存在吗?” (Rev.Mod.Phys.51,863-914(1979),p.907)。
的确,随着我们世界量子性质的发现,关于客观现实存在的古老哲学困境变得更加重要。波动函数可以以所需的精度预测测量结果,但是它是否与测量和观察者无关地存在,并且如何验证?
首先,有必要定义什么是观测和测量。为了测量物体的大小,我们在其上应用尺子,以测量温度-我们使用温度计来测量速度-向其发送电磁波。
在所有这些情况下,我们都需要被测对象与其他对象的交互,可以初步准备其状态,这样的对象称为测量系统。他们关掉温度计,准备好测量系统,放在腋下,进行交互,然后评估控制系统的状态已发生了多少变化。这是一个普遍原则,任何测量都是被测系统与控制系统之间的相互作用。
任何观察也是一种测量,观察到的东西是我们使用内置在人体中的测量系统获得的有关物体的信息,该系统也与物体相互作用。如果我们看着一个物体,那么我们将与该物体发出的光子发生相互作用,该光子落在眼睛的视网膜上,从而导致相互作用的复杂级联以及进入大脑的神经信号的发射。
« ? … . , , , . , … : “ , , ”».
«. » —
波的叠加原理告诉我们,当两个或多个波在空间中的一个点相遇时,相互作用的结果将是一个新波,这是它们的振幅之和。这样,测量结果将始终是被测波和测量系统的波函数的某种叠加。
现在出现一个合理的问题:如果我们接受一切都由概率振幅的波组成的断言,那么为什么我们
为了回答这个问题,让我们再次看一下双缝实验:电子一次飞过双缝并击中屏幕,并在屏幕上标记一个点;当重复多次此过程时,这些点形成的干涉图案对应于波通过两个缝的通过。

左:从波通过双缝隙时的干涉图案的动画来源。右:通过双缝后记录单电子的实验结果。资料来源:《新物理学》,2013年3月,第15卷。
但是,如果我们想知道电子穿过了哪一个狭缝,并在其中一个狭缝的前面放了一个测量装置,那么屏幕上的干涉图将消失,并且在屏幕上我们只会看到两个峰值。所有这些令人困惑,并且可能会给人一种印象,那就是有一条特殊的规则告诉电子,如果没有人在看,那么它就会以波的形式传播,当他们试图对其进行测量时,它会变成一个局部粒子。这听起来很奇怪,因为对于一个简单的电子而言,保持这么多复杂的规则根本不符合自然的精神。

一种漫画,将现象划分为量子和古典,颇为有趣。来源(http://www.bourbaphy.fr/zurek.pdf)
如果仅应用叠加原理,可以得到相同的观察效果吗?所以如果首先我们有一个波动函数来描述单个电子与屏幕相互作用的坐标
在一个波动函数的情况下,为了找到一个点处粒子相互作用的概率,我们将波动函数在此点的值乘以它自己的复共轭,虚部被抵消,我们得到经典的概率:
p ( x j ) = | ψ ( x j ) | 2 = z j ∗ z j = | z j | 2
在两条可能的路线重叠的情况下,我们将波浪函数的总和相乘:
p ( x j ) = | ψ 1 ( x j ) + ψ 2 ( x j ) | 2 =
= ( z 1 j ∗ + z 2 j ∗ ) ( z 1 j + z 2 j ) =
= | z 1 j | 2 + z 1 j ∗ z 2 j + z 2 j ∗ z 1 j + | z 2 j | 2
在上面的表达式中,除了复数模块外,我们还收到以下形式的条款:
z 1 z 2 = | z 1 | ⋅ | z 2 | [ c o s ( φ 1 + φ 2 ) + i s i n ( φ 1 + φ 2 ) ]
要了解两条替代路径的相位将如何相互作用,可以将相位想象成以给定速度旋转的箭头,随着波的传播,箭头的一整圈旋转对应于波长,旋转速度对应于频率。

黑色箭头显示了具有不同源频率的两个波包的相位“旋转速率”的比较。
由于通过将一个原图分开可以得到两个备选波函数,因此可以合理假设它们的频率和波长相同,并且所产生的波的箭头将以相同的速度旋转。基于此,当在屏幕上的某个点相遇时,相位差将仅取决于电波到该点的距离差。
这意味着,在与每个孔等距的位置处,波将与箭头的相同位置相遇,即在一个相位中,在此位置,我们将看到干涉图样的峰值,并且在行进距离差为该长度的一半处波浪-波浪的箭头将在相反的位置会合,并且将发生破坏性干涉,这将产生黑点。如果您再移动一点至差异是整个波长,则箭头将再次重合,依此类推。
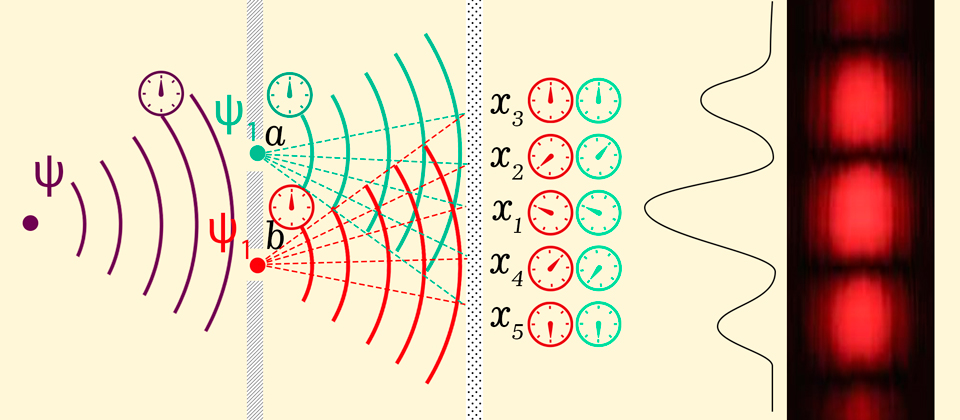
敲击屏幕的两种可能方式的出现导致原始波功能被划分为两个具有相同相位的功能,以带箭头的刻度盘的形式显示。相同的相位表示箭头的相同旋转速度。当在箭头的相同位置击中屏幕上的某个点时,波浪会产生相长干涉,如果箭头方向相反,则会产生相消干涉。
当我们测量时,干扰在哪里消失,电子会穿过哪个狭缝?通过检测器后,没有出现两个波函数,但出现了许多其他不同的波动函数,因为即使检测器是微观的,它仍将由大量原子组成,例如,甚至百分之一克的铁都包含约
也拿
p ( x j ) = | ψ 1 ( x j ) + ψ 2 ( x j ) + . . . + ψ n ( x j ) | 2 =
= ( z 1 j ∗ + z 2 j ∗ + . . . z n j ∗ ) ( z 1 j + z 2 j + . . . + z n j ) =
= ( ∑ j = 1 n z j ∗ ) ( ∑ j = 1 n z j )
为了清楚起见,我们将这些和乘以矩阵形式
[ ( z 1 ∗ ) ( z 1 ) ( z 1 ∗ ) ( z 2 ) ⋯ ( z 1 ∗ ) ( z n ) z 2 ∗ ) ( z 1 ) ( z 2 ∗ ) ( z 2 ) ⋯ ( z 2 ∗ ) ( z n ) ⋮ ⋮ ⋱ ⋮ ( z n ∗ ) ( z 1 ) ( z n ∗ ) ( z 2 ) ⋯ ( z n ∗ ) ( z n ) ]
我们得到的总数
这种不同步状态称为混合状态。)。尽管混合状态的波函数也会产生干扰,但干扰的结果将不再取决于波的传播距离,并且在屏幕的每个点上,人们都可以预期到相同数量的相长和相消干涉项,平均而言,它们将产生零贡献。 ... 正如气体分子的撞击不会使物体从其位置移开一样,因为物体在每个时刻都受到来自各个方向的冲击的次数大致相等。

波动函数的相干损失通过检测器后 1 导致屏幕上各点的干扰项的贡献为零,并且出现了与两个高斯峰的叠加相对应的模式。 d
在一般情况下,量子系统与外部环境的任何相互作用都不可避免地且非常迅速地导致状态的混合,并因此导致相位失步和替代状态的平均化(去相干)。
因此,我们对以下问题的回答是:为什么我们在正常条件下不观察宏观物体中的量子效应-为了获得宏观物体状态的叠加,必须将其与外界环境完全隔离开来,包括将其置于完全真空中,冷却至超低温并屏蔽不同领域,这在实践中很难实现。换句话说,薛定ding的猫即使在为产生其叠加所需的条件做准备时也会死亡,而放射性粒子会在很久以前就衰变,并用毒药破坏安瓿。
一点量子密码学
您的智能手机仍然没有量子处理器这一事实,您也必须归咎于退相干。毕竟,即使是最现代的量子计算机实现,也要占据整个房间,而它们的大部分设计都是低温冷却和屏蔽系统。
D-Wave 2000Q量子计算机结构图,来源。
但是,如果退相干在创建量子计算机时是一个大问题,那么在密码术中,测量过程中波动函数的不可避免变化就派上用场了。例如,如果我们将光子作为量子位,则根据其极化角,我们可以为零和一个选择两个不同的编码选项:
0 1 0 1
让我们将这两种编码方法指定为两个基础:
然后,如果光子飞过偏振器并撞击检测器,那么我们可以确定它是水平偏振的

左:垂直取向的光子被线性偏振滤光片阻挡。右:将偏光滤镜转到垂直极化的光子自由通过。来源。 90 °
到目前为止,一切都与经典图片编码系统完全一致。但是由于叠加原理,我们可以将对角光子表示为水平偏振和垂直偏振的组合,然后如果将其穿过定向为过滤垂直光子的偏振器,则输出将仅具有幅度为

左侧:对角光子(红色箭头),表示为电磁场的水平和垂直分量(粉红色和紫色箭头)。右:线性偏振滤光镜可阻挡对角光子的垂直分量,并输出水平偏振光子。来源
这意味着,如果我们在随机选择的基础上对每个下一个比特进行编码,则接收者还需要更改偏振滤光片的旋转,因为如果他测量以水平-垂直为基础编码的光子

穿过垂直线性偏振器,对角和反对角光子失去水平分量,输出是振幅为从原来的。来源。 1 / 2
第一个量子密码协议基于此原理-
因此,爱丽丝会收到一条加密的消息和一个密钥,如果收件人鲍勃也有一个密钥,则他可以再次执行XOR操作并获得原始消息。量子密码物理学只允许您交换密钥,因此在算法中
在完成量子密钥的传送后,有必要摆脱错误的,对于这一点,所谓的键筛分过程应用中,当爱丽丝发送鲍勃一个在其中键是通过经典信道简单地编码的碱基序列,在此之后鲍勃验证与他在其中所测量的光子的一个该序列在收到密钥后,将那些原来是错误的位置发送给爱丽丝。爱丽丝删除错误的位置,并将获得的密钥进一步用于加密。
量子技巧是,如果窃听者连接到通道,例如-Eve,它将截获一个光子,对其进行测量,然后将其进一步定向到Bob,然后在选择不正确的基础上测量被截取的光子,这也将不可避免地破坏该叠加。因此,即使经过筛选,在验证过程中,鲍勃的密钥中仍然存在可以检测到的错误,当爱丽丝通过经典渠道将其密钥片段发送给鲍勃时,如果验证没有发现错误,则可以放心使用密钥用于消息传递。
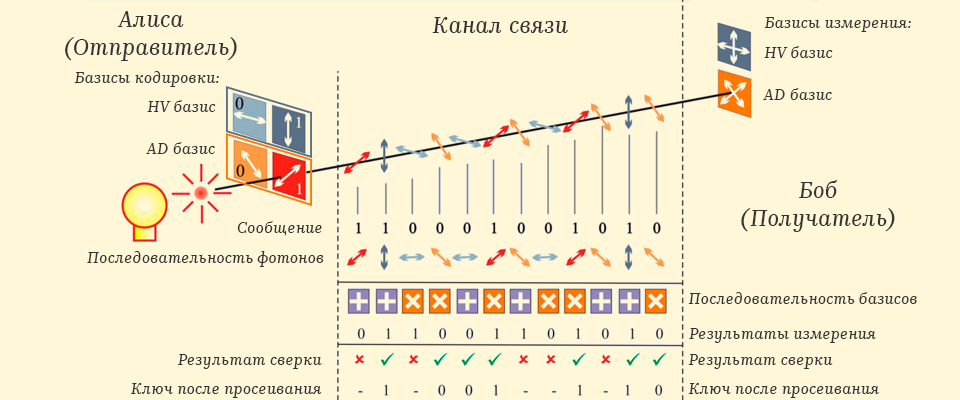
加密算法的逻辑图... 来源。 B B 84
结论
我希望从本文中您可以收集到一些信息,并对从一个奢侈的想法到量子理论如何成为我们宇宙最完整,最准确的物理模型之一有一个总体印象。最后,对于那些希望深入研究该主题的人,我想推荐一些资源和书籍:
- “物理学和哲学”-维尔纳·海森堡(Werner Heisenberg),对量子理论的理解,被其最杰出的创始人之一所见。
- QED-光与物质的奇异理论是杰出的理查德·费曼(Richard Feynman)的经典著作,该书取材于他60年代在加州理工学院(Caltech)进行的科普讲座。
- « » — , , , — .
- « » — - , , .
- Physics Videos by Eugene Khutoryansky — YouTube , , , .
- Minute phisics — , , , : , , .
- 3Blue1Brown-牛津校友格兰特·桑德森(Grant Sanderson)的频道,是易于理解的演示文稿和独特的概念可视化的完美结合,这些概念来自:量子物理学,线性代数,神经网络。格兰特(Grant)还是非盈利性项目可汗学院(Khan Academy)网站上提供的多元微积分课程的作者。