长期以来,数学家一直试图适应一些原则上无法解决的问题

我们想说一切皆有可能。在贾斯特·诺顿(Jaster Norton)的书《可爱与魔术亭》(Cute and the Magic Booth)中,国王拒绝告诉米洛他的目标是无法实现的,因为“如果您不知道这是不可能的话,那么很多事情就可能实现” [尽管这些是本书中其他人物的话。翻译 ]。但是在现实世界中,某些事情实际上是不可能的,我们可以用数学来证明。
人们以许多不同的方式使用“不可能”一词。他可以描述一些不太可能的事情,例如找到两副相同的洗牌牌。它可以描述由于时间,空间或资源不足而几乎不可能完成的任务,例如用手重写整个国会图书馆。永动机等设备在物理上是不可能的,因为它们的存在将与我们对物理学的理解背道而驰。
数学上的不可能是不同的。我们从明确的假设开始,并使用数学推理和逻辑得出结论,有些结果是不可能的。运气,毅力,时间或技巧都无法使任务可行。数学史上充斥着不可能的证明。其中许多被认为是最杰出的数学结果。但这并非总是如此。
对于可能的第一个证据的惩罚是严格的。历史学家相信在公元前5世纪。Metapont的Hippasus毕达哥拉斯(Pythagoras)的追随者,发现不可能找到可以测量正五边形的边长和对角线长度的线段。今天我们说,边长为1的正五边形的对角线长度是黄金比例,ϕ = 1/2(1 +√5)-是一个无理数。希帕索斯的发现对毕达哥拉斯的信条提出了挑战,“一切都是数字”,因此传说说,希帕索斯要么淹死在海中,要么被逐出毕达哥拉斯人的行列。
一个多世纪后,欧几里得将线和圆提升为几何的基本曲线。随后,几代几何学家仅借助指南针和标尺就绘制了各种各样的东西-划分角度,绘制垂直线等。但是,某些看起来很简单的结构使希腊几何感到困惑,其结果是获得了神话般的地位,并激怒了2000多年的数学家。这些问题是将任意角度分为三个部分,构造一个立方体的侧面,该侧面的体积是给定立方体的两倍,构造所有正多边形,还构造一个正方形,其面积等于给定圆的面积。
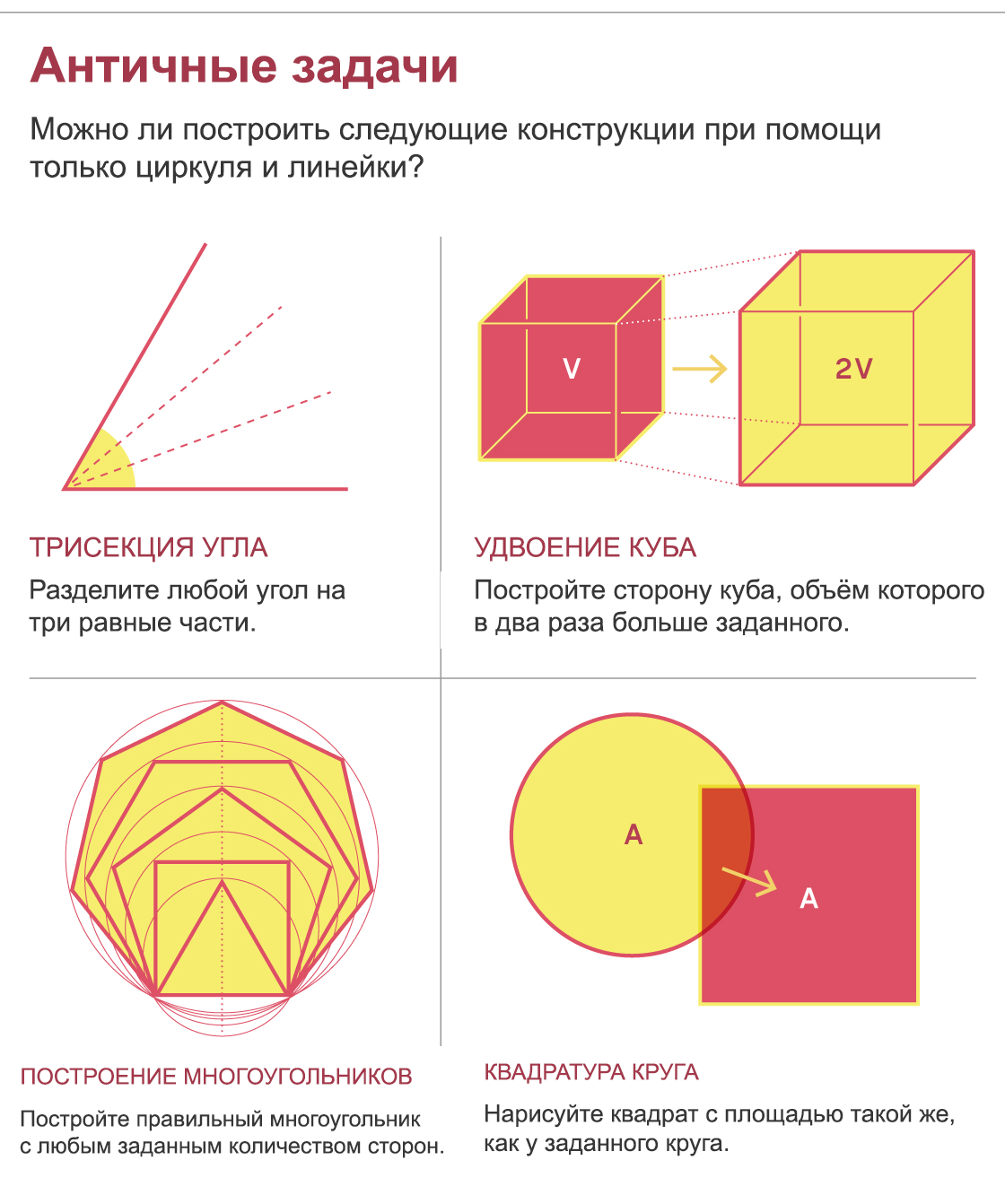
尽管这些问题本质上是几何问题,但并非无法解决这些问题的证据。需要新的数学来证明不可能解决它们。
在17世纪,雷内·笛卡尔(Rene Descartes)做出了一项基本发现:如果我们仅将自己限制在指南针和尺子上,就不能绘制任何长度的线段。如果我们从长度为1的线开始,我们只能构造其长度可以使用整数,加法,减法,乘法,除法和平方根表示的线(如黄金分割率)。
因此,寻找证明不可能解决几何问题(即无法构造特定对象)的证明的策略之一将是表明无法以这种方式表示最终图形的特定段的长度。但是为了严格说明这一点,需要后来出现的代数。
两个世纪后,笛卡尔的同胞皮埃尔·洛朗·凡泽尔(Pierre Laurent Vanzel)使用多项式(系数和变量的和加到幂上)和其根(使多项式等于零的变量)来解决这些经典问题。例如,在将立方体加倍的问题中,体积为单位立方体两倍的立方体的边必须等于... 这是多项式x 3 -2的根,因为...
Wanzel在1837年证明,要使用罗盘和直尺构造线段,其长度必须是无法分解的多项式的根,并且其幂(变量的最高幂)为2的幂。例如,黄金分割率是二阶多项式x 2 -x-1的根。但是x 3 -2是三阶多项式,所以你无法建立。因此,Wanzel得出结论,将立方体加倍是不可能的。
同样,他证明了不可能使用经典工具将任何角度三等分或构造某些规则的多边形-例如,一个七边形多边形。有趣的是,所有三种不可能的证明都张贴在同一页面上。正如艾萨克·牛顿(Isaac Newton)和阿尔伯特·爱因斯坦(Albert Einstein)患上了奇迹般的年纪时,这种情况可以称为“ pagina mirabilis”(奇迹页)。
证明余下的问题是不可能的,即对圆进行平方,需要一些新的东西。 1882年,费迪南德·冯·林德曼通过证明其超越性,即不是任何多项式的根,证明了关键点-不能构造数字π。
这些经典问题可归因于声誉不佳,并被认为是诱使数学家撞上不可能的坚石的警报器。但是我认为它们的灵感启发了几代创造性思想家。
这同样适用于由于过桥这样简单的操作而引起的新的不可能完成的任务。想象一下,就像我的许多学生一样,您住在匹兹堡,这座“桥梁之城”。任何喜欢冒险的骑自行车的人都可能想知道,从家中开始骑行是否能穿越匹兹堡主要河流的22座桥中的每座,只返回一次。
1735年,普鲁士市长为伦纳德·欧拉(Leonard Euler)设定了类似的任务,仅对国王尼斯堡(现在的加里宁格勒)设定了任务。这个城市的七座桥连接着河流和岛屿的三岸。起初,欧拉(Euler)认为这个问题不是数学问题:“这种解决方案与数学关系不大,而且我不明白您为什么希望数学家将它交给您而不是别人。”
但是,很快欧拉证明了解决这个问题的可能性,并在此过程中创建了一个新的数学领域,他称其为排列的几何学-我们今天称之为拓扑。他意识到具体的细节-桥梁的确切位置,土地的形状等。 -不重要。只有他们的联系很重要。后来,数学家使用我们今天所谓的图来完善欧拉的公式。连接性的概念是学习社交媒体,互联网,流行病学,语言学,路线规划等的核心。
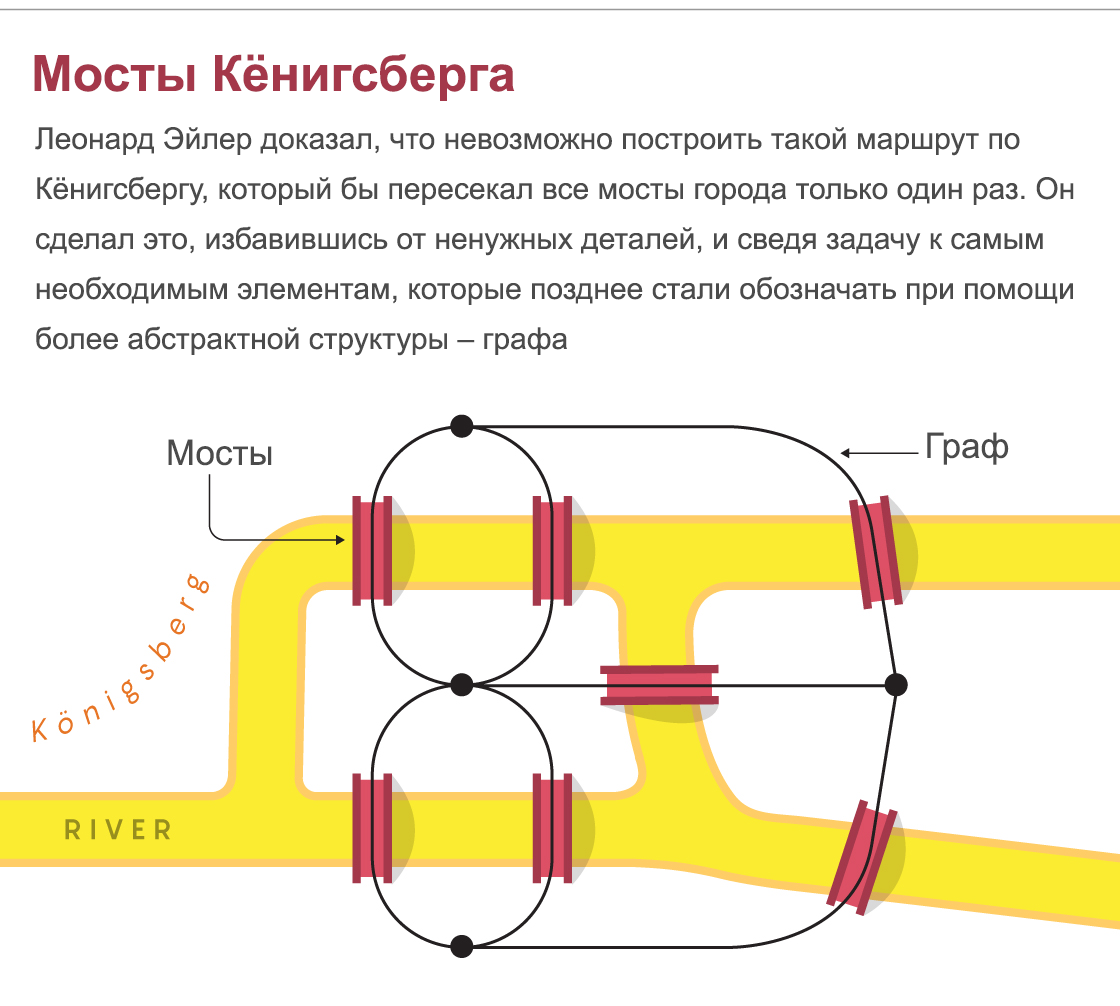
柯尼斯堡(Königsberg)桥梁:伦纳德·欧拉(Leonard Euler)证明,沿着柯尼斯堡(Königsberg)修建一条仅跨越城市所有桥梁一次的路线是不可能的。为此,他消除了不必要的细节,并将问题简化为最必要的元素,后来又开始使用更抽象的结构(图)来指定问题。
欧拉的证明非常简单。他认为,每次我们进出然后离开一块特定的土地时,我们都必须消除两座桥梁。因此,每块土地都必须连接偶数个桥。但是,由于通往科尼斯堡(Königsberg)各个区域的桥梁数量奇多,因此不可能建立这样的路线。同样,通向匹兹堡阿勒格尼河上盖斯岛的三座桥梁也使得无法建立理想的自行车道。
正如这个问题表明的那样,不可能不限于抽象数学。它们可能产生现实世界的后果,有时甚至是政治后果。
最近,数学家转向了格里曼德制的概念。在美国,每次人口普查后,各州都必须重做选区。但是有时执政党以荒谬的方式改写其边界,以最大限度地发挥其政治权力。
许多州对“紧凑”区的要求没有严格的数学定义。 1991年,丹尼尔·鲍尔斯比和罗伯特·波普尔提出4πA/ P 2作为测量面积A和周长P的紧凑性的一种方法。这些值的范围从圆形教区的1到长周边的变形县的几乎为零。
同时,尼古拉斯·斯蒂芬诺普洛斯(Nicholas Stephanopoulos)和埃里克·麦吉(Eric McGee)在2014年引入了“绩效差距”,以衡量地区改革计划的政治完整性。两种不同的选票策略是让选区中的反对派获得不到50%的选票,或者是100%左右的选票。这些策略中的每一种都会使反对派失去合适的候选人,或者在没有选出的候选人上浪费选票,从而失去选票。效率差距描述的是丢失的相对票数。
这两种措施都有助于识别搬运工。但在2018年,鲍里斯·阿列克谢夫(Boris Alekseev)和达斯汀·米森(Dustin Mixon)事实证明,“有时候,形状怪异的县可以实现较小的效率差距”。就是说,从数学上讲,总不能吸引县同时满足鲍尔斯比-波普的要求和效率差距的完整性是不可能的。
但是,检测和防止秘密管理技巧是一个快速发展的领域,吸引了许多有才华的研究人员。与古代问题或柯尼斯堡桥梁问题一样,我相信,接管工夫的问题将激发创造力并为数学的发展做出贡献。