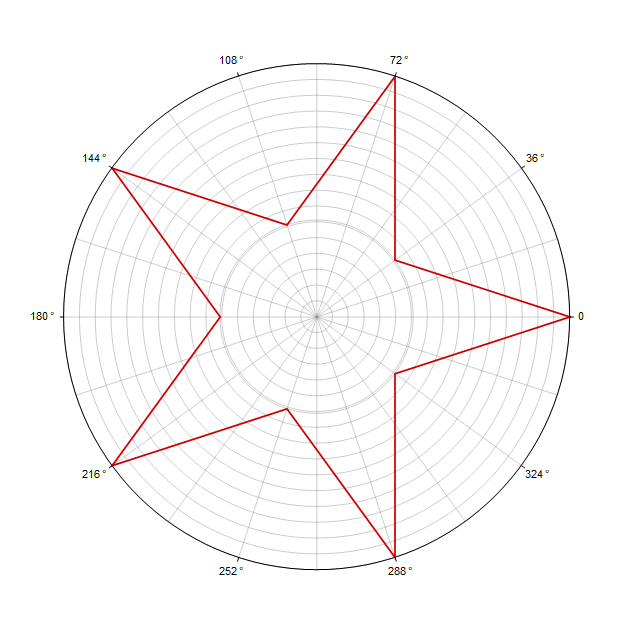
极坐标中的等边多边形的公式看起来非常简单
并具有以下参数:
是角度;
是凸顶点的数量;
确定边在一条直线上通过多少个顶点。负值也是允许的-符号将确定恒星向哪个方向弯曲;
刚度-在我们得到一个圆,而与其他参数无关,因为具有直线的多边形,中间值为至圆形和多边形之间的中间图形。
使用此公式,您可以通过两种方式绘制星星:
1)
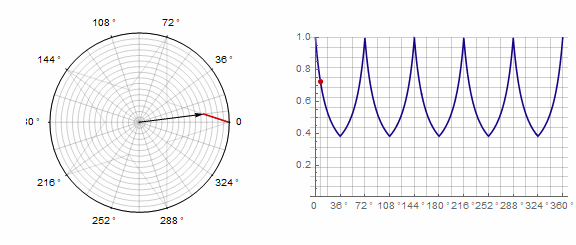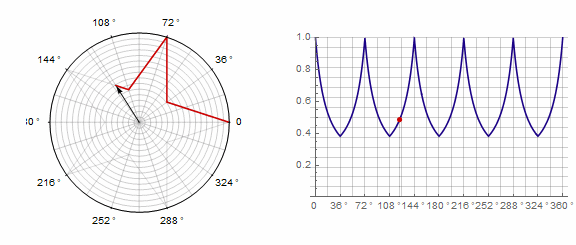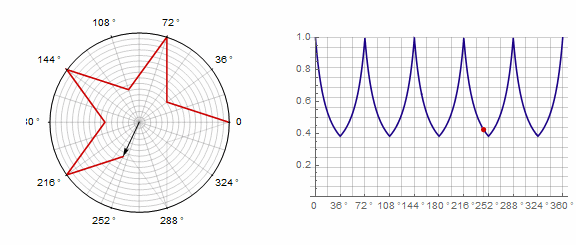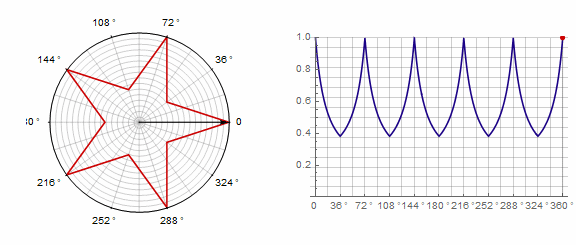
2) 。在这种情况下,您需要转两圈而不是一圈:
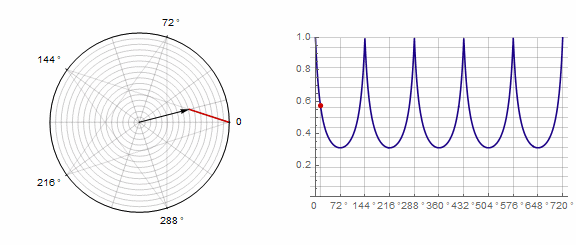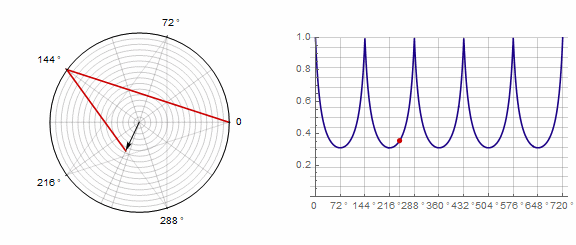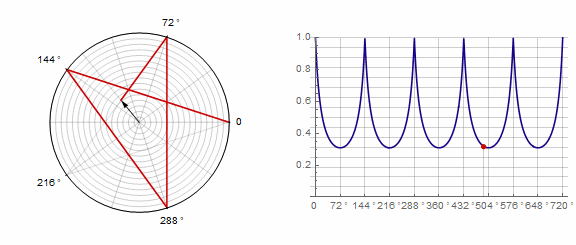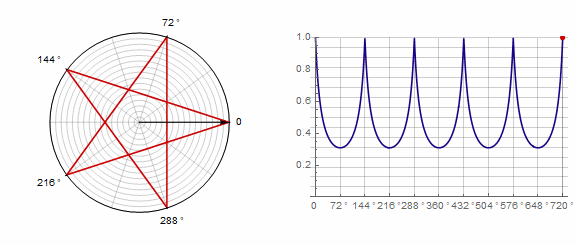
参数 对多边形的影响如下(此处从-1变为5):
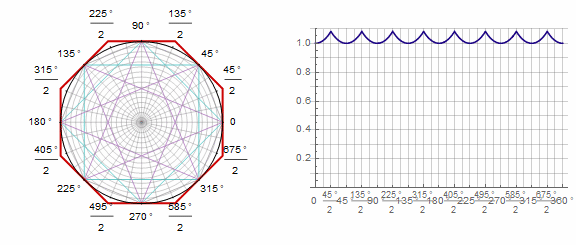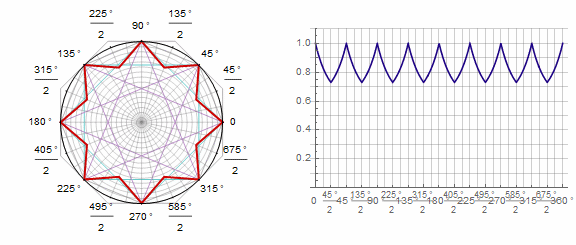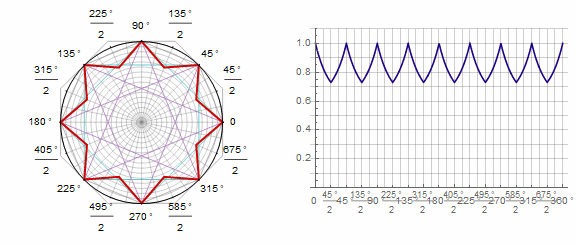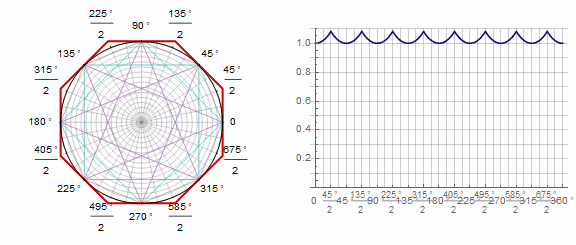
参数 动画中的k:
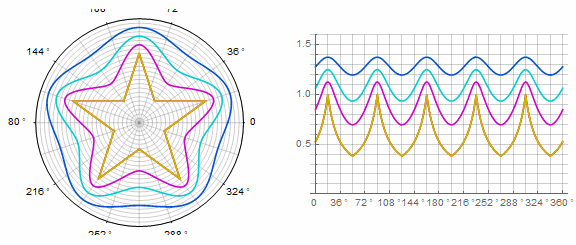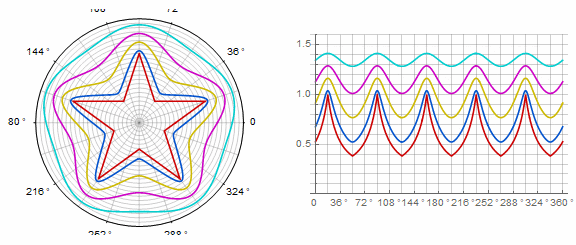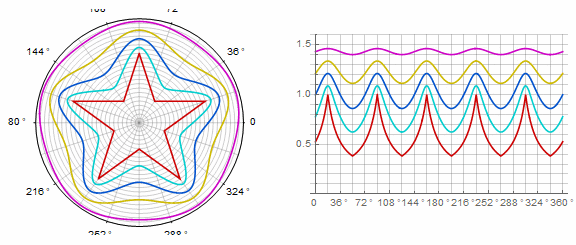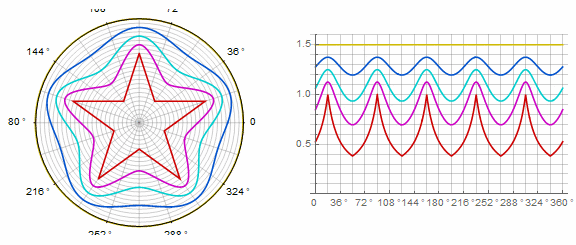
复杂的形式和修改
您可以用复杂的形式重写原始公式,并且尽管其中存在虚数单位,半径值仍将保持有效:
乍一看,这似乎毫无意义,因为公式变得有些麻烦-但不要下结论。首先,其中没有反正弦,这完全改变了公式的数学含义,并让您对星状多边形的构造有不同的看法。其次,它还可以用于获得特殊情况的紧凑公式,例如。第三(也是最有趣的),它可以被创造性地修改并获得其他意想不到的形式。为了使半径中可能出现的虚部出现而不会引起计算歧义,可以通过乘以来将其立即减小为笛卡尔坐标。。以下是一些修改的示例:
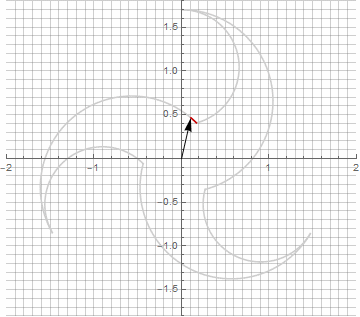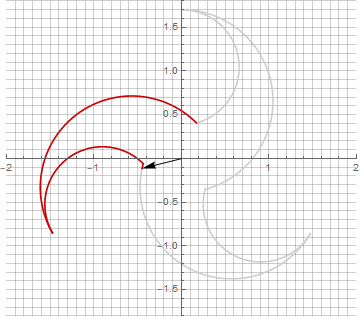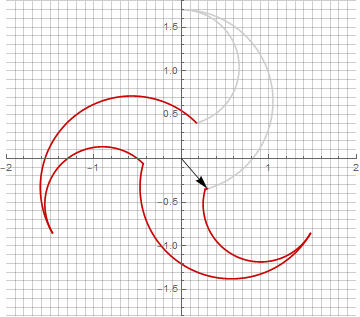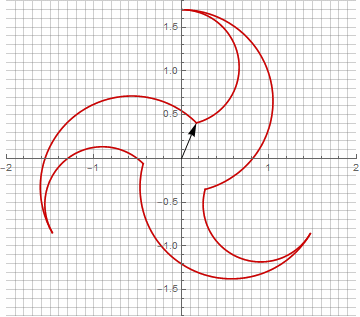
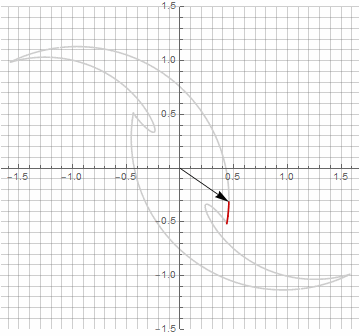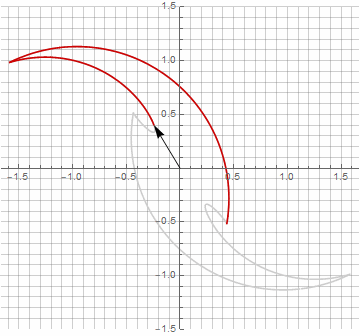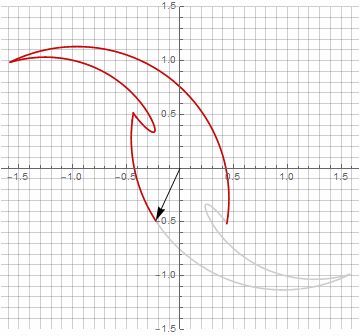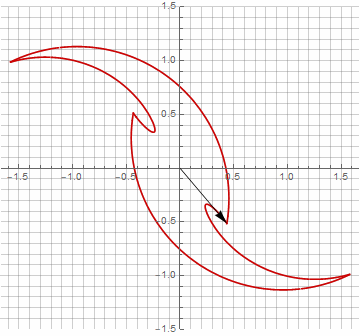
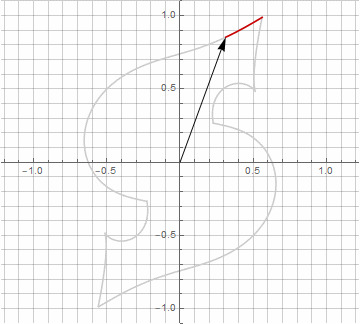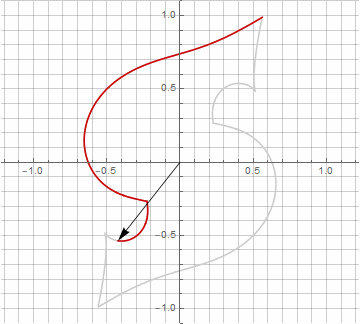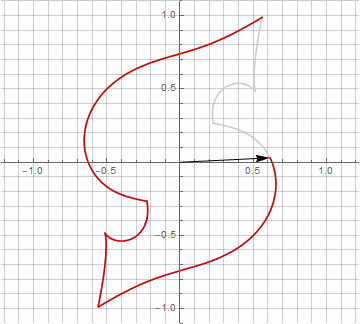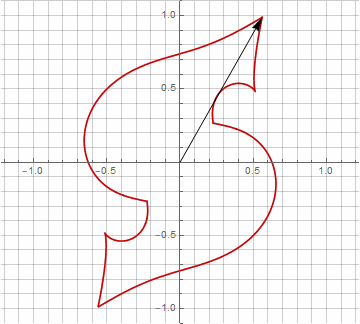
您可能已经注意到,向量的旋转不再是均匀的-正是由于半径中虚部的出现。
四边形和东西
我们的公式有一个奇妙的特殊情况-正方形,其公式可以写成
要么
(选择最喜欢的那个)。
在稍微发达的情况下,您可以定义圆和正方形之间通过点的中间图形 表面上
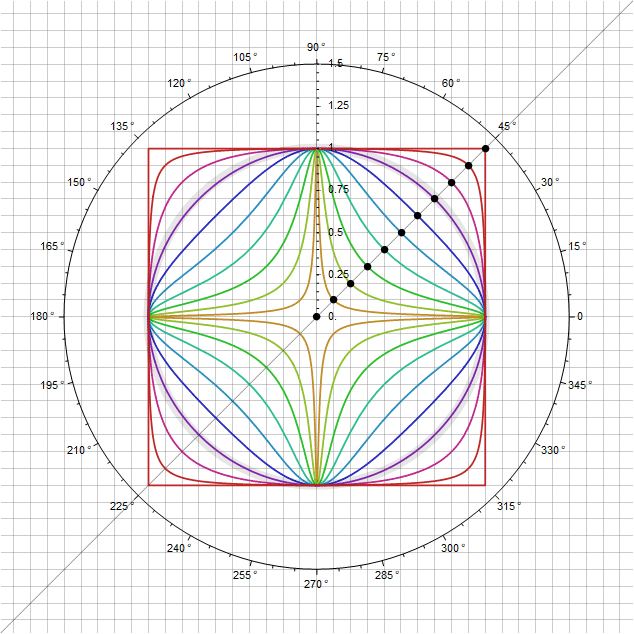
您还可以为这些形状添加变化,同时保持它们通过点的条件 -直接调节参数本身 取决于角度,以便在通过对角线时其乘数等于1。例如,代之以 功能 ,我们将获得一个附加参数 通过它可以调整其他弯曲。特别是对于 您得到以下信息:
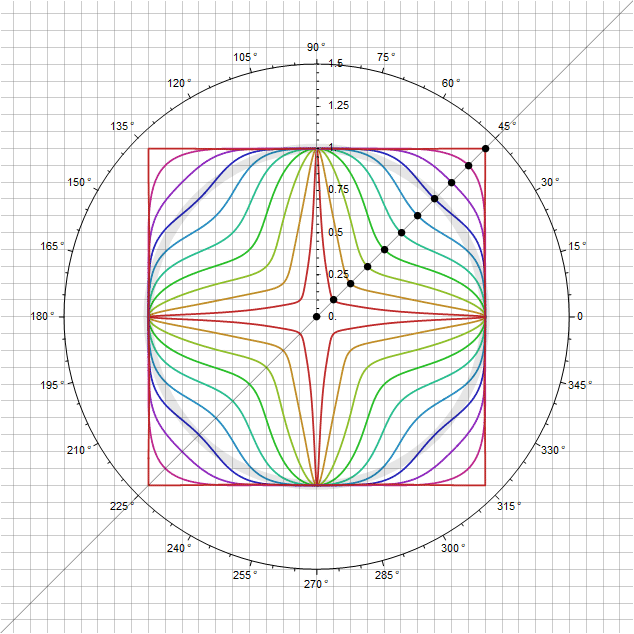
在更扩展的情况下,您不仅可以定义正方形,还可以定义矩形,并且仍然以极坐标定义:
甚至计算其面积(通过椭圆积分):
注意
( ) , .
这将使轮廓从圆形过渡到矩形,并控制截面面积。这里面积是恒定的:

在这里,该区域呈指数增长:
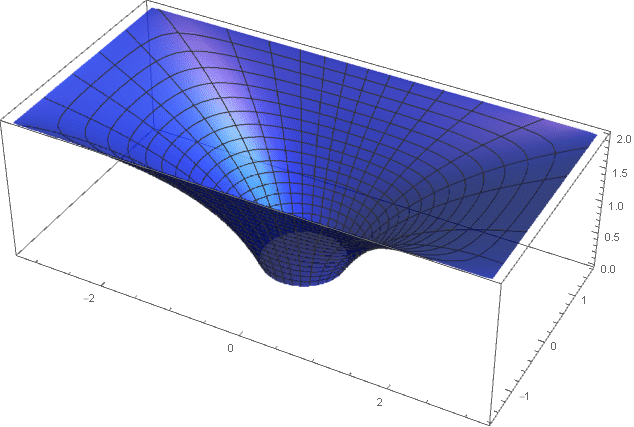
转到笛卡尔坐标
极坐标中的任何公式都可以通过笛卡尔坐标中的方程式表示,并且至少以两种方式表示-取决于图形边界上的渐变形式将改变。为此,只需通过坐标的反正切来计算角度,然后通过减去半径就可以通过半径矢量将公式变为常数
或除法
第二种选择是可取的,因为它沿多边形的侧面给出了直线渐变。
注意
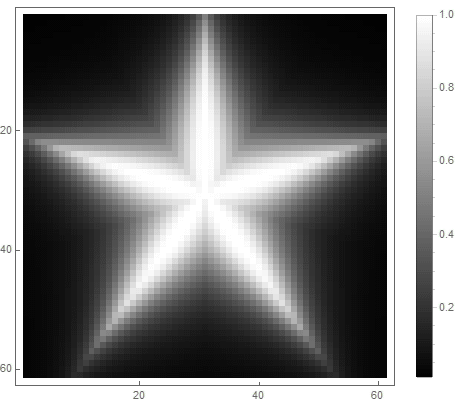
等式右侧的公式的值(在第二种情况下)将从 之前 如果点 进入图中,并从 无限广告-如果没有。通过选择不同的功能将其转换为亮度,您可以获得不同的光栅化选项。对于指数( 对于第一个 对于第二种选择),我们得到
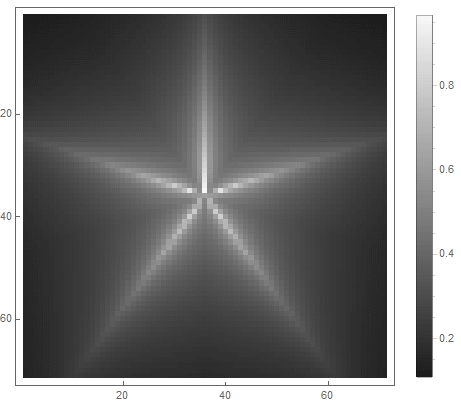 |
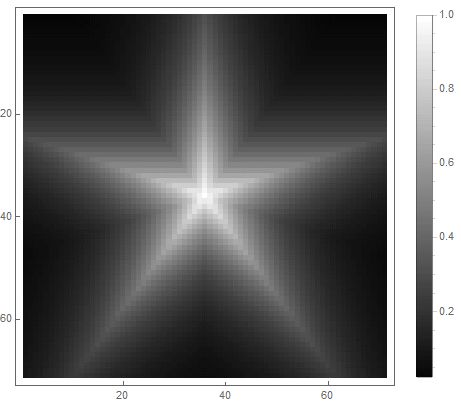 |
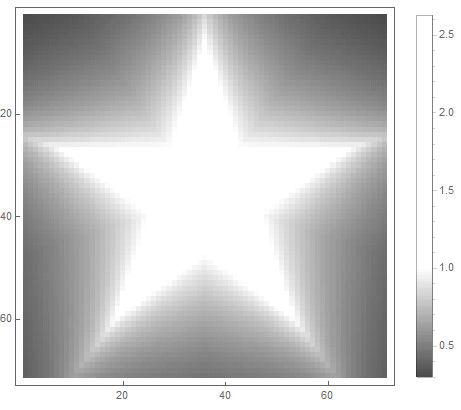 |
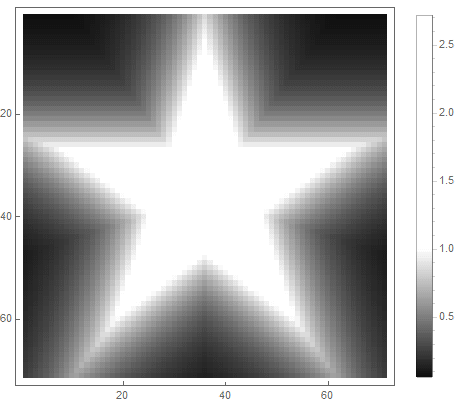 |
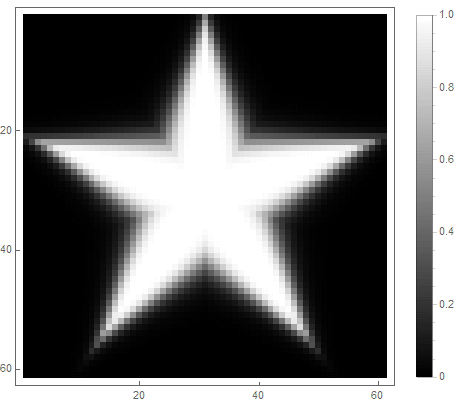
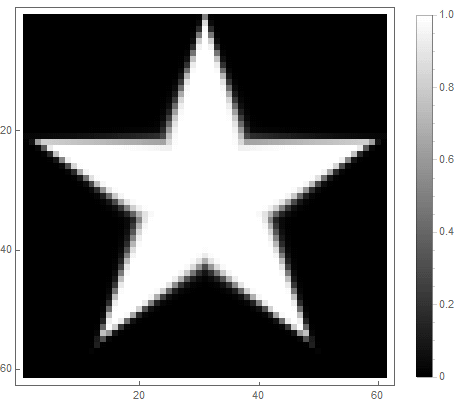
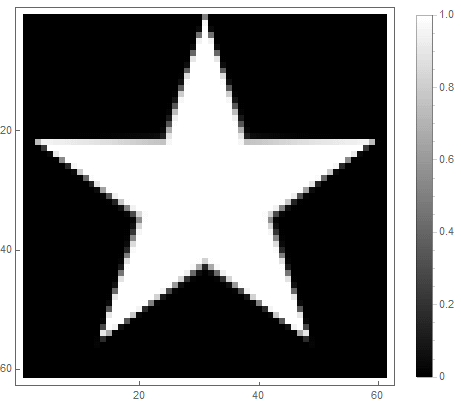
可以使用经典的低通滤波器 ,其中 -滤波器的阶数,它决定衰减的程度。
对于第一种选择:
 |
 |
 |
 |
第二:
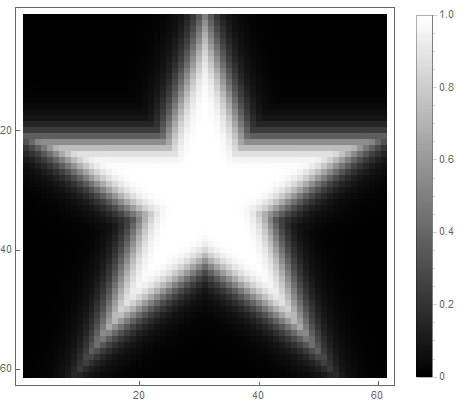 |
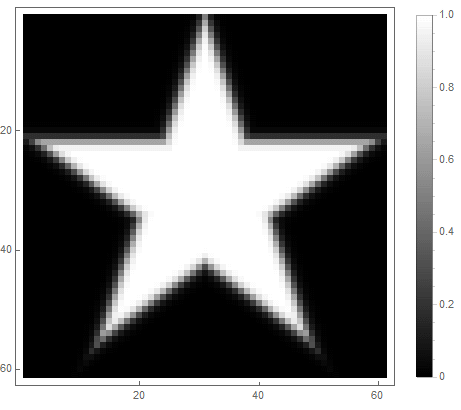 |
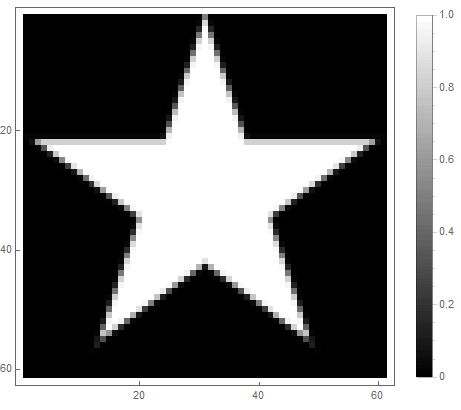 |
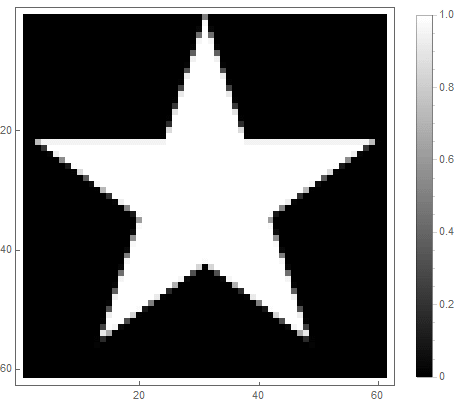 |
您也可以通过显式设置插值边界来使用分段连续函数。
除了这样的栅格化之外,您还可以设置变形-例如,将棋盘格挤压成圆形:

甚至将其拉到一个球体上:

式
附录:公式的来源
数学文本中讲故事的经典风格包括引理/定理及其证明的交替-好像可证明的陈述是从上面的启示出现在作者的脑海中的。而且尽管这有一定道理,但在公式出现之前通常要先进行一些研究工作,对公式的描述比形式证明可以更好地理解其含义。陈述的真实性又可以通过导致它们的步骤的真实性来追溯。
因此,在这里也是如此-如果文章以复杂形式的公式开头,那么其外观将是非显而易见的和违反直觉的,并且声明的属性将需要其他证明。但是在三角形式的记录中,很有可能可以追溯其出现的历史。
1)我们从最简单的情况开始-在极坐标中绘制直线。为此,您需要求解方程其解决方案很明显 ...
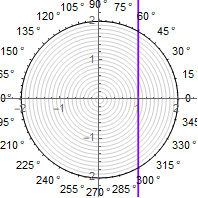
2)此外,割线参数需要被“循环”以提供直线上的扭结。正是在这个阶段,其他解决方案使用除法余数形式的“脏黑客”。它还使用顺次采用正弦和逆正弦函数-
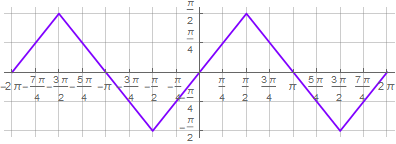
这种方法使您可以对所得公式执行标准数学运算,
例如
:
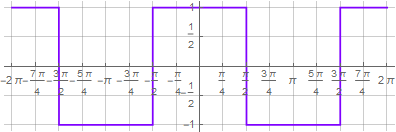


由于使用了相同的符号,因此可以使用三角函数的复杂表示形式将极坐标中的平方函数简化为更美观的外观。在Wolfram Mathematica中,可以使用TrigToExp和ExpToTrig函数完成此操作:
代码
↓
Sec[1/2 ArcSin[k Sin[2 \[Phi]]]]^2//TrigToExp//ExpToTrig//Sqrt[#]&//FullSimplify
↓
多亏了相同的记录,您可以使用附加的乘数获得圆和方之间的平滑中间图形 由于正弦参数不足一个- :
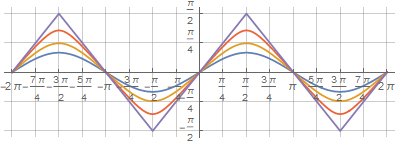
为了使函数与给定点相交,您只需要制作一个方程式并重新计算 :
代码
↓
Solve[(Sqrt[2/(1+Sqrt[1-k Sin[2 \[Phi]]^2])] /. \[Phi]->Pi/4)==x, k] /. x->k
↓
3)参数 和 实际上,只是以创新的方式添加了它们,并且对其效果进行了实验研究。
4)通过转到参数视图并“拉伸”轴,很容易获得矩形
但是之后 现在将不再意味着角度 只是一个参数,它通过投影到坐标轴上来描述矢量。要返回极坐标,您需要找到向量的长度(通过平方和的根),角度(通过比率的反正切),并通过 并替换结果表达式 ...
代码
↓
↓
↓
With[{r = Sqrt[2/(1 + Sqrt[
1 - Sin[2 t]^2])]}, {Sqrt[(a r Cos[t])^2 + (b r Sin[t])^2],
ArcTan[(b r Sin[t])/(a r Cos[t])]}] // Simplify
↓
Solve[ArcTan[(b Tan[t])/a]==\[Phi], t]
↓
Sqrt[2] Sqrt[(a^2 Cos[t]^2 + b^2 Sin[t]^2)/(1 + Sqrt[Cos[2 t]^2])]
/. t -> ArcTan[(a Tan[\[Phi]])/b] // Simplify
↓
简化这样的公式已经更加困难了,这将需要几个阶段:
- 通过替换去直角坐标 ;
- 变成指数形式;
- 简化;
- 进行反向替换 和 ;
- 回到指数形式;
- 简化。
结果,我们得到以下公式:
代码
↓
Sqrt[2] Sqrt[(a^2 b^2 Sec[\[Phi]]^2) /
((1 + Sqrt[Cos[2 ArcTan[(a Tan[\[Phi]])/b]]^2])
(b^2 + a^2 Tan[\[Phi]]^2))] /. \[Phi] -> ArcTan[x, y]
// TrigToExp // Simplify
// # /. {x -> Cos[\[Phi]], y -> Sin[\[Phi]]} &
// TrigToExp // Simplify // FullSimplify
↓

结论
如您所见,即使在多边形这样简单而普遍的事物中,您也可以找到并提出新的事物。故事还没有结束-一般情况下的面积公式仍然未知,任意的,不仅仅是规则多边形的面积公式仍然未知,并且扩展到幂级数和三角级数的过程也没有考虑。同样,对于3维情况,可能存在类似的公式。
因此,如果您被告知数学中的所有事物都是已经发明的,并且仅存在普通人无法理解的问题,请不要相信。真正的数学家不了解许多纯粹的实际问题,或者由于周围没有足够的炒作而对他们的解决方案不感兴趣,或者因为他们已经对实现它们的解决方案有了粗略的想法。不要害怕解决其解决方案在Wikipedia中不可用的问题,不要害怕发布其解决方案,也不要害怕阅读有关一切无用性的文章下的评论。
PS在这里下载Mathematica的原始文档。