
继续讲这个话题,我会说我看过其他Habr作者关于这个话题的出版物。人们对问题很感兴趣,但是没有人愿意涉足理论。像先驱发现者一样行动。如果他们获得新的成果和成就,那就太好了,但是没有人为此奋斗。
但是实际上,事实证明它比已知情况更糟糕,没有考虑很多因素,在不建议这样做的情况下使用了该理论的结果,并且总体上看起来并不十分严峻,尽管应该理解的哈伯并不为此而努力。读者不能也不应该充当过滤器。
原始备选方案集,其评估和评估
已知找到解决方案的问题仅在选择的多种选择情况下出现。要考虑决策情况,制定特定的决策问题(DP),选择一种解决方法,就必须具有一些有关替代方案,偏好关系的初始信息。
让我们在小节中说明存在哪些获取方法。备选方案具有许多会影响决策的属性(功能)。例如,对象的属性(重量,体积,硬度,温度等)的指标可以是定量的或定性的。
让一个来自Ω的备选集的某些属性用一个数字表示,即存在一个映射ψ:Ω→E1,其中E1是实数的集合。然后,用指示符来表征这种属性,并且就指示符而言,数字z =ψ(x)被称为替代项的值(估计)。
为了评估替代方案,有必要测量指标。
定义。某种特性指标的度量应理解为以某些单位为该指标的各个级别分配数值。在这种情况下,测量单位的选择很重要。
因此,例如,如果首先以立方米为单位测量容器的某个部分的体积,然后以升为单位进行测量,则指示器的本质不会改变;只有单位数会改变。这些属性度量可以缩放,乘以或除以该属性度量的常数。
另一方面,有些属性的指示符不允许对它们的值进行此类操作。物体的加热程度以温度为特征,以度为单位。该指标的值+ 10°和–15°不能判断温度为+ 10°的人体比其温度为–15°的人体要加热多少次。
从这些示例中,有可能(并且很重要)得出结论,即体积和温度指数是指不同类型的属性,在z =ψ(x)的值上,某些转换f(z)= f(ψ(x))是允许的或不允许的...
即,将一组可允许的变换f(z)作为确定测量某种属性(属性)的指标的比例的类型的基础。对研究人员强调的功能指标进行一次或另一次测量,我们来确定要进行测量的比例尺类型。
如果没有正确解决此问题,我们可能会在处理观察结果时承认对测量结果的错误处理。当指标值经历给定规模类型所允许的一组转换之外的转换时,就会发生这种情况。
定义。测量尺度是协议接受的各种大小的相同值的值序列。
让我们更详细地考虑秤的主要类型。
1.标称标度。当研究人员处理某些特征所描述的物体时,使用名义标度。根据给定对象是否具有某个特征值或不存在某个特征,将该对象称为一个或另一类。
例如,如果我们在谈论人,那么特征的价值(特征的尺度是由两个性别值构成的:男性和女性)允许我们明确地将每个人分配给某个类别。因此,该标尺称为分级标尺。这样的标志可以使一个人被称为,例如,老师,木匠,或者根据该职业的指标的值来称呼他人。
这种情况下的规模是由所有专业的名称构成的。显然,在这个规模上,零表示没有,尽管该学科中没有专业可以使他精确地分配给没有专业的人类别。尽管以方便起见,通常按字母顺序排列,但专业名称并没有按此比例排序。
基于这些考虑,这样的标度被称为命名标度。
在此范围内,有效的值转换都是一对一的函数:f(x)≠f(y)<=> x≠y。
2.顺序秤。如果所研究的特征(例如材料的硬度)在物体上表现出不同并具有无法具体测量的值,但是人们可以明确判断任何两个物体其表现的比较强度,那么他们说该特征的值是按序数尺度测量的。一个典型的例子是矿物质的硬度。未定义刻度上的参考点为0。
特征值定义如下。这对中较硬的矿物在另一方留下了划痕。根据此特性值的所有矿物可以按以下顺序排序:第一个是最硬的,第二个更硬,它仅在第一个上留下划痕,第三个在前两个上留下划痕,依此类推。
序数标度和标称值之间的差异在于可以对特征的值进行排序,而名义规模的值甚至无法订购。序数刻度的缺点是它不成比例。
不可能回答一种矿物比另一种矿物难多少倍的问题。序数标度的允许变换包括具有以下特性的所有单调递增函数:x≥y => f(x)≥f(y)。
3。间隔刻度(interval)。与顺序量表的不同之处在于,对于它们描述的属性,这不仅有意义,并且等价关系和顺序关系也有意义,而且各种属性的定量表现之间的间隔(差)之和也有意义。一个典型的例子是时间间隔刻度。
可以添加和减去时间间隔(例如工作时间,学习时间),但是添加任何事件的日期毫无意义。
另一个示例,长度(距离)-空间间隔的比例是通过将标尺的零与一个点对齐来确定的,而在另一点进行读取。这种类型的秤还包括摄氏,华氏和Reaumur的温度秤。
在这些比例尺中,线性变换是允许的,(x-y)/(z -v); ∓他们应用程序查找数学期望值,标准偏差,不对称系数和位移矩。
4.差异量表(点)差异量表与顺序量表的不同之处在于,区间量表不仅可以判断大小大于另一个,还可以判断有多少个,实质上,这是相同的绝对量表,但是其值是相对于绝对值(x-y)<(z -v)的一些值; ∓
5.关系量表...一组允许的变换包含所有相似性变换的比例称为关系比例。参考点固定在此比例尺上,允许更改测量比例尺。
让此比例尺测量对象的长度。在这种情况下,您可以从以米为单位切换到以厘米为单位,将度量单位降低100倍。显然,在这种情况下,以相同单位测量的两个物体A和B的长度L(A)和L(B)的比率在改变单位时不会改变。
以这种尺度衡量的特征指标的值可以
回答这个问题,即一个对象比另一个对象更能表现出多少次特质。为此,有必要考虑值L(A)/ L(B)= k的比率。
如果比率大于一个(k> 1),则第一个对象A的属性指示符的值是B的k倍,如果k <1,则对象B的属性指示符的值是A的1 / k倍。是乘以一个正整数,仅此而已。
6.绝对规模。所有比例中最简单的比例是仅允许一个转换f(x)= x的比例。这种情况对应于测量对象属性指标的唯一方法,即对象的简单重新计数。
该比例尺称为绝对比例尺。当注册对象x时,除此对象外,我们对其他任何东西都不感兴趣。绝对比例尺可以视为某些其他比例尺的特定实现。
决策任务。获取关系矩阵
我们列出了ZPR的可能设置,包括:
- 替代品的线性排序(链的顶部是最好的);
- 突出最佳选择;
- 突出显示最佳选择的(无序)子集;
- 突出显示最佳选择的有序子集;
- 替代品的部分排序;
- 有序(部分有序)替代方案的拆分;
- 替代品的无序划分(分类)。
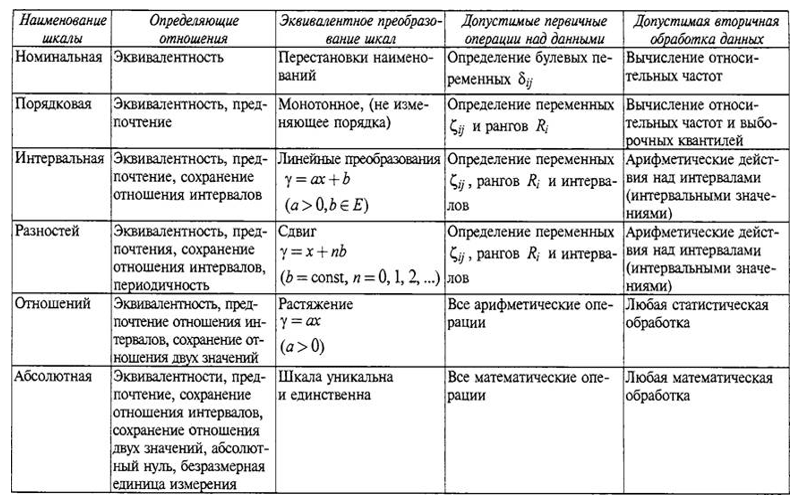
在对不同规模的替代品属性指标的测量结果进行分析的基础上,可以用不同的方式表示测量结果[1,5]。
1.分类表。该表是在以名义比例进行测量时获得的,它是一个表,其行是:对象的名称,列是类的名称 ...等。如果对象属于该类,则在类1,类2等列中放置1;如果不属于该类,则放置0-(对象表类)。
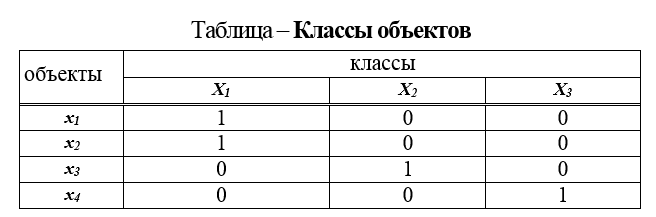
方阵。它的第i行对应于第i个元素集合Ω的x i和元素的第j列。在第i行和第j列的交点处,如果对象比对象优先,如果对象为零优于对象,1/2如果有物体和漠不关心,什么也没放-如果对象是无与伦比的和无法比较。
下面的矩阵中提供了这种偏好关系的示例。
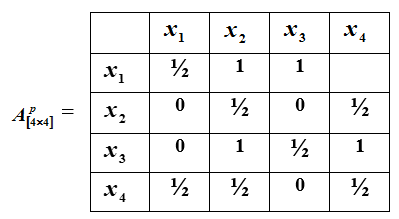
3.指标表。在关系量表中获得。选择将要测量的指标的属性。进行这些特性的测量,并将测量结果记录在表格中。
在列中表格的p 1,p 2,p 3,p 4优先级比率包含用于评估对象的属性指标的值和。
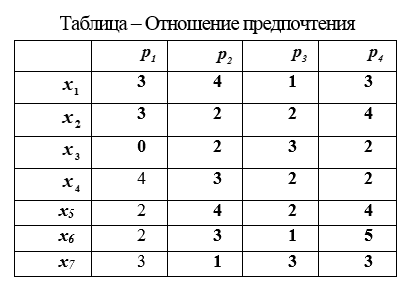
在以这些表示形式获得测量结果之后,我们需要以关系形式显示结果,因为我们将依靠发达的二元关系理论的仪器来求解ZPR。
偏好表到二进制关系矩阵的映射如下:
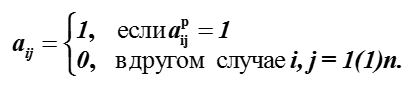
从偏好关系矩阵 4个替代示于表中。偏好关系将是矩阵,看起来像这样:
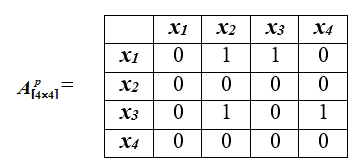
计分卡到偏好率矩阵的映射如下: 如果:
1)对象所依据的指标数量比对象优先大于对象所依据的指标数量优于对象;
2)针对对象所有指标均未取最小可能值。
3)条件1暗示那些对象所针对的指标并不比对象差构成了所考虑所有指标的大部分。
但是,如果满足此条件,则可能会根据对象所针对的那些指标比对象更糟糕,差异是显着的;为了减少在优先考虑x时的这种情况,引入了条件2。
解决决策问题的方法
让我们在收到初始数据之后,在备选集上具有关系R ... 任务是做出决定。主要方法是对替代方案进行线性排序(排序),即按价值,适用性,重要性等从“最佳”到“最差”的降序在链中构建替代方案。
比率R可以是:
- 完全不及格的态度;
- 偏序关系;
- 线性顺序。
只有在关系R呈线性的情况下,偏好的结构才能满足任务。在这种情况下,可通过构建有序集合的线图直接获得集合Ω中的替代项的排名。在图中,替代,将严格高于替代方法 如果愿意的话。
对于完全和传递关系提出的问题的解决方案,是使用方法(算法)对备选方案进行排名,而对于部分订单,则使用线性重新排序算法。这些算法将在下面的段落中讨论。
替代品的排名。令关系[Ω,R]完整且不可传递。完整性属性意味着所有替代方案集合中的彼此可比。仅当偏好图G [Ω,R]包含轮廓时,才可能存在非传递性。
必须变换关系图的结构,以便消除轮廓形式的逻辑矛盾。如果我们假设存在一个与R有关的轮廓 然后在对替代品进行排名时 应该位于更高的位置 ,这导致了矛盾。
让我们介绍以下语句[1,5]。
令B'和B“是形式为G [Ω,R]的图的两个任意轮廓,则如果某个元素 єB'占主导地位 єB'',然后是任何元素 єB'任何元素都占主导地位 єB''。
该提议可以将集合R划分为m个子集这样
因此,对集合的替代项进行排名的问题分为两个阶段:
1)选择图的轮廓,即 将集合Ω划分为子集
2)在第一阶段选择的轮廓元素的排名。
识别图形
轮廓的算法有一种简单的算法可以找到图形的轮廓[1]。让
从图论[10]得知,对于“稳定”矩阵的所有相同行的每个系统,对应于位于一个轮廓中的图的顶点的子集。将相应的顶点分组为类,我们将原始集合Ω划分为子集
显然,在这些子集中可以找到这样的子集
然后,我们使用相同的原理在其余子集中找到最佳子集,并将其放在第二位。我们将
继续执行此过程,直到所有子集都进入排名为止。
令偏好关系R通过矩阵在集合Ω上给出

关系图R在图5中示出。G。
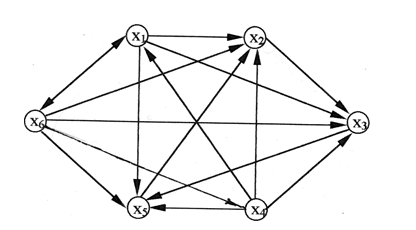
数字:D.非传递关系图R
要实现对一组元素进行排名的第一阶段,必须选择图G [Ω,R]的轮廓。这可以通过将图的邻接矩阵提高到连续的幂直到矩阵匹配来完成。
我们得到
接下来,我们依次计算矩阵的递增幂,并将它们与相应维的单位矩阵相加,直到矩阵停止变化为止:
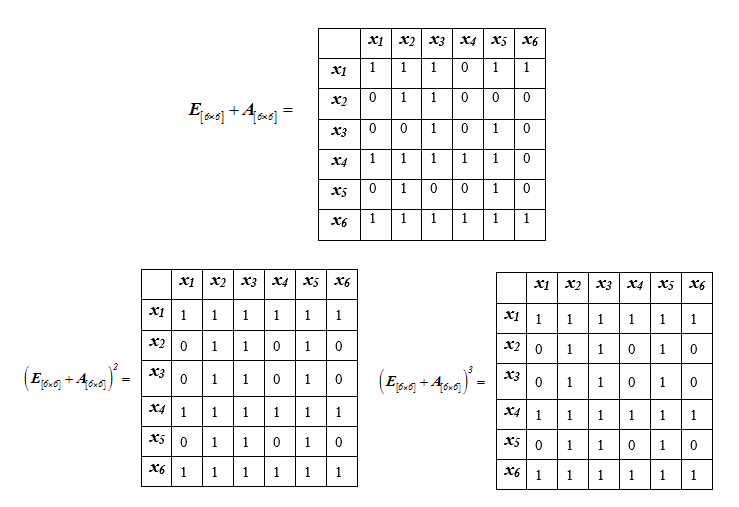
因为
要素
因此,我们将集合划分为m = 2个类
这将意味着子集的优越性
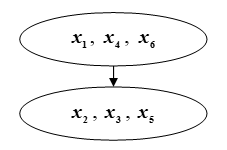
数字:质量控制。在第一阶段选择的轮廓的排序对轮廓
元素进行排序的算法。是否可以将关系的元素排列在相同的轮廓中,或者它们彼此相等,或者它们之间是否存在足够细微的差异以区分它们?事实证明,这种可能性通常存在[1]。
让我们用
让
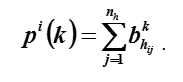
元素i的第k阶相对强度被理解为分数
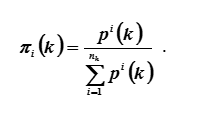
随着k无限增大(k→∞),数
由于Perron-Frobenius定理[1],该限制始终存在。轮廓邻接矩阵的归一化特征向量与其极限向量一致。因此,向量
不用计算积分力就可以找到
其中,λ是特征方程的最大非负实根
应注意的是,当矩阵乘以数s> 0以及将其与形式为sE的矩阵相加时,非负不可分解矩阵的归一化特征向量不变。
然后通过减少相应矢量分量的值对轮廓元素进行排序
我们将对集合的元素进行排名
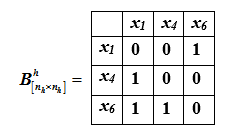
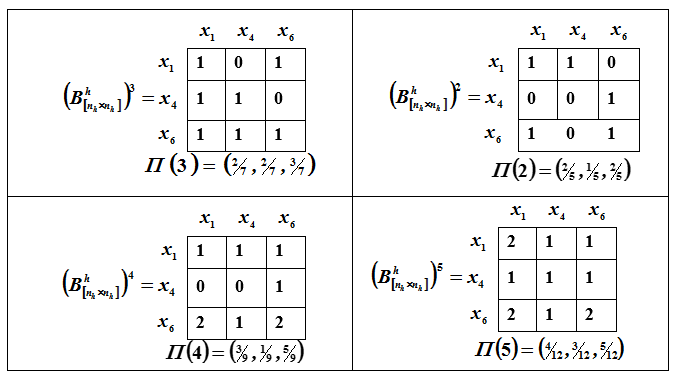
元素一阶积分力的向量
物品等级
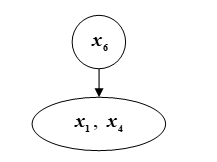
数字:R.元素排名
让我们找到表征第二,第三,第四和第五阶力的向量。
图中显示了排名的图形表示。P.
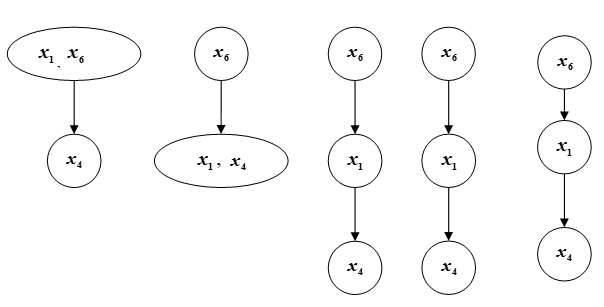

图C-链
以类似的方式对集合B2的元素进行排名,我们得到图9中所示的结果。对。
结合集合1和2的元素等级的结果,我们进入了集合Ω的元素的最终排序(图C)。
严格部分订单的线性重新排序
令由专家的个人判断汇总而得到的关系R(下文中的图A)为集合Ω的偏序关系。在这种情况下,Ω是有序集合。备选方案的线性排序的构造是按顺序量表获得其“功能”的全局评估。
由于某些原因,某些专家无法根据偏好比较某些替代方案。在这种情况下,集合Ω上的聚合关系R将不是线性顺序。显然,这导致了从Ω到替代方案的线性重新排序问题。这种重新排序通常可以通过多种方式进行。
对于部分排序,存在多个线性排序表示结构中的“本征排序”对于单个线性排序是不够的。因此,有必要解决部分订单的线性重新排序的问题。令R为偏序。
定理(Spielrein [5,10])。集合上的任何阶数R都可以扩展为该集合上的线性阶数。
Spielrein定理的推论:子集的任何线性重排
如果X是Ω中的子集,由不可比的替代组成,则X的任何线性排序都可以扩展为整个集合Ω的线性排序。在这种情况下,R的阶数以线性阶数表示
根据Spielrein定理,在集合Ω上存在一个编号
在一般情况下,查找线性附加排序的问题被简化为查找原始部分有序集的所有允许的编号。您可以写出Ω中所有元素的排列,其中会有n个!并针对每个条件检查“较大”元素对应于较大数字的条件。但是,这种查找所有其他订购的方法非常费力且效率低下。
对于具有阶次R的有序集合Ω,如果没有严格更大的元素x,则集合Ω的元素x'被称为最大值。如果x> x'对任何xΩ都不成立。如果元素x''比任何其他元素x大,则称元素x''为有序集合[Ω,R]中的最大元素。对于任何xΩ,x''> x [5]。
如果有序集合中有最大元素,则为最大元素。如果有序集具有单个最大元素,则它将是最大元素。在部分排序的集合中,允许多个最大元素。
对于n元素集Ω的任何编号,数字N分配给最大元素。如果通过删除此类最大元素之一已知从Ω获得的所有子集的所有编号,则可以获取集合Ω的所有编号。相同的技术应用于每个子集[7]。考虑一种用于构造有序集[Ω,R]的所有编号的算法。
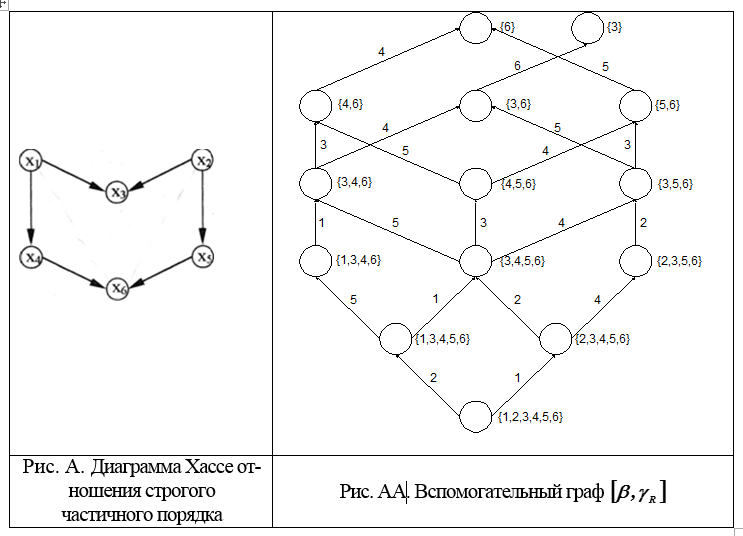
1.构造一个有序集[Ω,R]的辅助图[β,γR],其顶点满足以下条件:
a)是Ω的子集;
b)对于任何两个子集X,Yєβ,都是正确的:(X,YγR)如果
可以通过删除子集X的最大元素之一从子集X获得子集Y(图A和AA)。
2.对于集合γR的每个单元素子集,写下其唯一编号。为了获得子集X的所有编号,有必要枚举所有相邻的子集,并且对于每个这样的子集继续其所有编号。结果,将获得集合Ω的所有编号,即 的顺序R.所有线性扩展
的问题是要找到一个偏序,该图,其中示于图的所有线性额外排序。答:没有这方面的信息,例如,替代方案是否占主导地位
1.我们从集合开始构造一个辅助图[β,γR]
2.我们形成表格。AAA以查找作为图[β,γR]顶点的子集的所有编号。从上到下一行一行地填写表格。每行是表左表(表AAA)中记录的子集的编号。
3.组成由k个元素组成的子集X的编号时,有必要重写所有先前记录的(对于先前子集)子集YєγR(x)的编号,并为与Y补充X的元素分配一个数字。
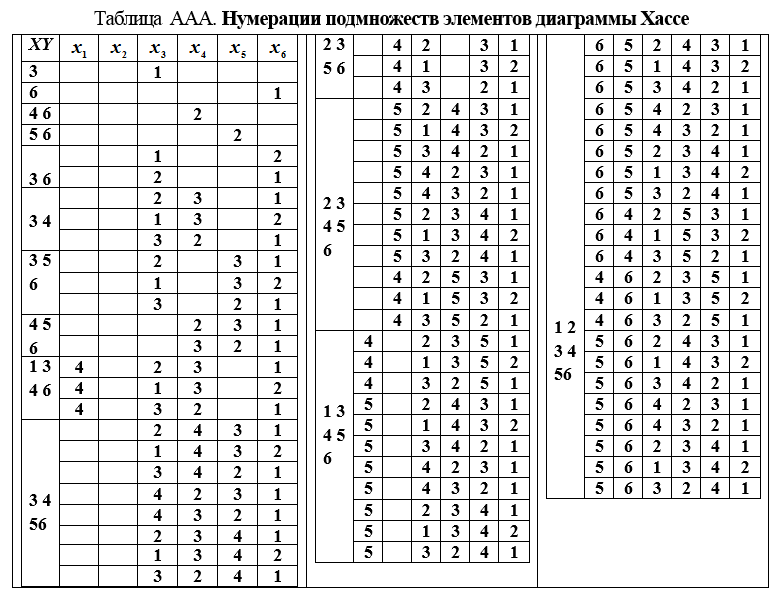
最后一个(下部)块(表AAA)包含集合Ω的线性重新排序的所有编号。这些重新排序的图形表示如图2所示。AAA。
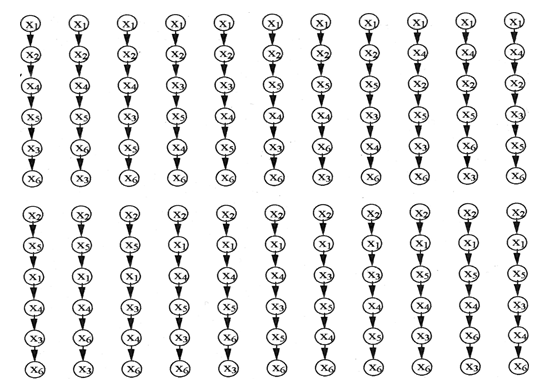
数字:AAA。预购的图形表示
应该注意,一组6个元素上有6个线性订购!或720,并以图7所示的曲线图给出的关系对设置的Ω进行线性重新排序。AA,总共22个,这也足以做出决定。
是否有机会减少此类选择的数量?是的,有。
为了减少线性附加订购的数量,您需要使用附加信息。
附加信息
令[Ω,R]为初始关系,则附加信息可以表示为集合Ω上的关系δ,其中条件(x,y)єδ,即,(x> y)被解释为一条消息,表明对象x支配了对象y;
然后,比率δ可以被视为以二进制比率δ给出的一组关于优势信息的类似消息,使用附加信息时有两种可能的情况:
- 关系图R∪δ包含轮廓;
- 关系R∪δ的图不包含轮廓。
在第一种情况下,使用
早先考虑的排序算法,以给定比率R∪δ对集合Ω进行线性排序。
在第二种情况下,使用
上面考虑的线性重排序算法执行具有给定比率R∪δ的集合Ω的线性排序。应当注意,不包含轮廓的关系R∪δ可以是非传递性的,因此不是部分顺序的。
为了成功摆脱这种情况,必须以Hasse图的形式给出附加信息δ和初始比率R。没有明确指示传递链接。附加信息的值将由线性附加阶数在使用时减少多少倍来确定。
例如,如果收到信息,
为所有对元素解决此问题
关于此对中的关系的附加信息的值越高,差异越小
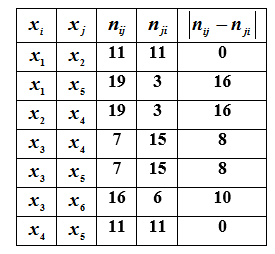
从表的分析可以看出,最有用的
信息将是关于成对关系的信息
结论
ZPR的制定和解决方案只有在多种选择和最佳选择的情况下才有可能。如果没有选择,请按照您所处的道路走。
决策者根据自己的偏好做出决策,这由偏好关系来描述。关系的存在使您可以建立用于研究的数学模型。通过使用不是专家的其他信息,可以消除偏好的不确定性。
注意对象的属性指标的测量和估计值的考虑。给出了经常被忽略的各种比例的示例。
列出了ZPR的可能公式以及解决方案所需的信息。
通过一个具体的数值示例,显示了代数方法在求解ZPR方面的应用,而没有使用统计样本和经验处理方法。
该方法基于定理的结果,该定理涉及将偏序扩展为线性(完全)阶的可能性。
二手文献清单
1. Berge K.图理论及其应用。 -M .:伊利诺伊州,1962.-320羽
2. Vaulin AE计算机安全问题中的离散数学。第一部分SPb .: VKA以A.F. Mozhaisky的名字命名,2015年-219羽
3. Vaulin AE计算机安全问题中的离散数学。二。 SPb .: VKA以A.F. Mozhaisky的名字命名,2017年-151羽
4. Vaulin AE信息计算系统的研究方法。问题2.-L。:VIKI他们。莫扎伊斯基(A.F. Mozhaisky),1984年-129羽
5. Vaulin AE信息计算系统的分析方法和方法。第1期。– L。:VIKI im。莫扎伊斯基(A.F. Mozhaisky),1981年-117羽
6. Vaulin AE数字数据处理方法:离散正交变换。 -SPb。:VIKKI他们。 A.F. Mozhaisky,1993年-106羽
7. Kuzmin VB在明晰和模糊二元关系的空间中构造群解。-M.:Nauka,1982年。-168羽
8. Makarov IM等人,“选择与决策理论”-莫斯科:菲兹马特利(Fizmatlit),1982年–328页,第52页。
9.罗森V.V. 目的-最优性-解决方案-M .:无线电和通讯,1982年– 169页。
10. Szpilraijn E Sur Textension de l'ordre partiel。-Fundam。数学,1930年,第16卷,第386-389页。