🤛🏽 🛍️ 🍮 选项：挂断电话，布朗移动。极客教育计划，第7部分 🙂 🚋 👩‍🎨

这是关于期权的故事的第二部分，我们将处理看涨期权飙升，无市场套利的情况，熟悉对冲和复制的思想，并讨论布朗运动是什么以及它与模拟金融资产利率随时间变化的行为有何关系。

将进行一些数学运算以获得对这些细节的更好理解。

这篇文章是我的视频讲座“ Put-call悬停和没有套利的条件”，“ Brownian motion ”的抄录，是金融科技课程Finmath的一部分。

挂断电话。使用无套利条件分析工具组合价格的示例

因此，从上一部分开始，我们知道到期时的看跌期权和看涨期权的付款情况（可以行使期权所提供的权利的时间），但是我们也想知道如何计算其他时间段的期权。为此，我们需要使用更复杂的数学仪器来构建数学模型。但是，在进行此操作之前，让我们先看一下电话平价关系，该关系并不复杂，在实践中非常有用。

回想一下，欧洲期权是一种合同，根据该合同，买方在未来的指定时刻获得了以预定价格买卖某些标的资产的权利，但没有义务。

标的资产可以是股票或货币汇率。基础资产的市场汇率称为现货，在公式中，该现货当时的价值

t

$t$ 表示为

S_{t}

$S_t$ ...

授予购买基础资产权利的期权被称为看涨期权。出售权是看跌期权。期权授予将来达成交易的权利的价格称为行使价，表示为

K

$K$ ...

合同中可以使用该期权的预先约定的时间是该期权的到期时间（到期）-

T

$T$ ... 到期时标的资产利率的值表示为

S_{T}

$S_T$ ...

让我们建立到期的付款时间表。我们有一定的基础资产-到期价格：

S_{T}

$S_T$ 以及付款

P

$P$ 我们收到。付款时间表将在这些坐标中

S_{T}, P

$S_T, P$ ... 开始吧

K

$K$ -轴上的打击水平

S_{T}

$S_T$ ...

我们要绘制的第一个选项是看涨期权。我们购买了看涨期权。

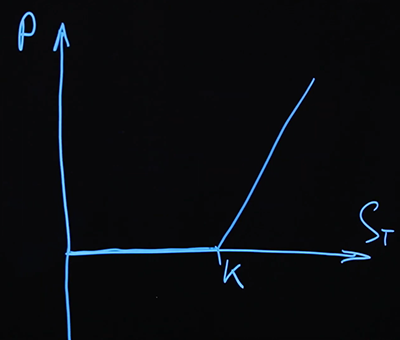
这也称为“多头”看涨期权，该期权上的加号位置。但是我们也可以出售期权，这就是所谓的short。

我们要抽出的第二个选择将是卖空。

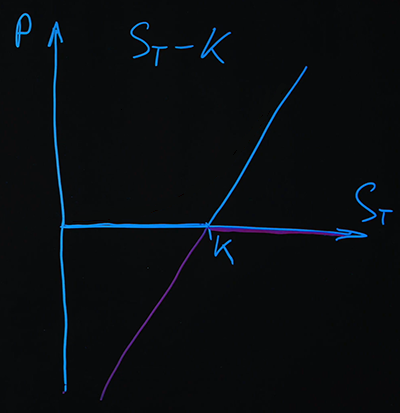
在该图中，我们可以看到，当我们将这两个付款相加时，我们得到了一个简单的线性函数，其定义为（

S_{T} - K

$S_T-K$ ）。可以通过分析获得相同的结果。我们有一个带加号的看涨期权头寸和带减号的看跌期权头寸：

C - P

$C-P$

让我们使用我们已经知道的分析公式：

m a x (0, S_{T} - K) - m a x (0, K - S_{T})

$max(0, S_T-K)-max(0, K-S_T)$ ...

为了扩大括号，我们必须考虑两种单独的情况

S_{T} > K

$S_T>K$ 和

S_{T} < K

$S_T<K$ ...

我们有以下系统：

{\begin{cases} S_{T} - K - 0, S_{T} > K \\ 0 - K + S_{T}, S_{T} \leq K \end{cases}

$\begin{cases} S_T-K-0, S_T>K \\ 0-K+S_T, S_T≤K \end{cases}$

在这两种情况下，您将获得相同的简单公式：

S_{T} - K

$S_T-K$ ...

因此，无论在到期时变现基础资产的价格如何，在任何情况下都用相同的公式描述付款。再次提醒您，我们提取的付款是到期时期权的付款（因此是成本）。对于其他时间点的期权价格，它们由其他一些更复杂的功能来描述。我现在有条件地画它们。

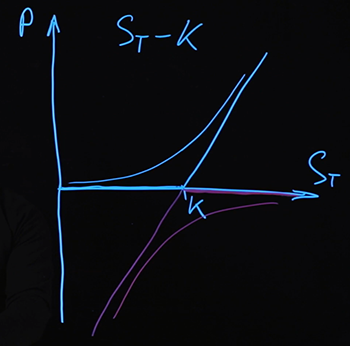
我们知道，对于到期时的这种组合，支出由公式确定

S_{T} - K

$S_T-K$ ，任何价值

S_{T}

$S_T$ ... 如果我们发现其他一些组合的工具将在到期时给予相同的付款，那么我们可以说这种组合的工具和组合的成本

C - P

$C-P$ 应该是一样的。

如果不是这种情况，那么今天您可以购买这些组合中的更便宜的组合，并出售更昂贵的组合，从而获利。并且由于这两个组合在到期时给出相同的支出，并且我们以相反的符号表示它们，所以总支出保证为零。仅仅由于市场工具价格的不平衡而产生的保证收入而没有风险的交易称为套利。... 用于计算工具价格的数学理论通常包括市场没有套利的假设。这个假设与现实足够吻合。市场上的仲裁机会（如果确实存在）不会持续很长时间。查找和使用它们并不容易。因此，通常这种假设会奏效。

从市场无套利的条件出发，可以得出以下结论：

C - P

$C-P$ 随时会

t \leq T

$t≤T$ （不仅仅

T

$T$ ）费用与任何工具组合相同，但其付款时间为

T

$T$ 将相等

S_{T} - K

$S_T-K$ ... 通过购买基础资产可以轻松实现这种组合

S

$S$ 并借入一定数量的钱，以便在到期时需要返还等于

K

$K$ ... 在处理金融工具时，此类债务等同于出售零息债券（债券），该债券将支付

K

$K$ 在这一刻

T

$T$ ... 您可以在本系列以前的文章中了解有关债券和利息的更多信息（货币价值，利率类型，贴现率和远期利率。针对极客的教育程序，第1部分，以及债券：息票和零息票，收益率计算。针对极客的教育程序，第2部分） ...

因此，来自看涨期权的投资组合和来自看跌期权的投资组合等于基础资产的多头和空头债券的组合，这将使每个到期日的派息与面值

K

$K$ ...

C_{t} - P_{t} = S_{t} - B_{T} K

$C_t-P_t=S_t-B_TK$

该比率与我们可以为基础资产利率建立的模型无关。它甚至不取决于我们如何考虑折价，这是由于市场上没有套利。我们汇总了一个投资组合，考虑了所有可能的选择权，以及到期后可能需要支付的费用，发现在所有将来的选择权中，其花费完全相同。因此，如果另一个投资组合具有完全相同的到期支出，那么它们的价格应该相同。

因此，我们得到了看涨期权和看跌期权组合的比率。我们编制了一个投资组合，研究了到期时将要支付的款项，发现该款项由一个线性方程式描述。与看涨期权和看跌期权的支付功能不同，每个看涨期权都有两个部分，越来越少

S_{T}

$S_T$ ...这使您可以构建更简单的工具组合，在任何情况下都可以在到期时获得相同的支出。这两个投资组合的价格在任何时候都将是相等的，而不仅仅是在到期时。市场没有套利的条件可以保证这一点。如果市场上存在套利且不满足这种平等要求，那么我们可以相应地购买其中一种投资组合，出售另一种投资组合，并保证获得胜利。该比率不取决于我们可以为基础资产的价格建立的任何数学模型。在任何模型中都必须满足该比率。

您也可以这样看这个比例。我们汇总了具有相同风险的几种资产的投资组合。一方面可以重写公式以收集承担与基础资产相关的风险的资产。也就是说，我们可以消除这些工具固有的所有风险，即与标的资产的未来价格相关的不确定性，确切地知道这样一揽子计划的价值。

C_{t} - P_{t} - S_{t} = - B_{t} K

$C_t-P_t-S_t=-B_tK$

这种消除风险的方法称为套期保值。我们组成了包含了一些相同风险的几种工具的投资组合，但是我们按一定比例选择它们，以使这些风险相互平衡，从而摆脱了这种风险。其他更复杂的对冲策略中也使用了这种想法。所考虑的情况非常简单，它仅允许您使用某些选项组合。

如果我们从另一侧看这个想法，那么我们可以通过其他工具来表达其中一种工具。例如，如果我们在市场上有一件东西，看跌期权，那么我们将自动收到看涨期权。在这种情况下，它将是复制-我们通过其他产品复制了一种产品的付款方式。套期保值和复制彼此紧密相关，在数学上，它们是非常相似的计算。

在这种情况下，我们的情况非常简单，为了完全对冲风险或复制支出，我们只需要创建一次投资组合，然后等到到期时，就已经保证了支出。这称为静态复制（静态对冲）。这是一种罕见的情况，通常不起作用。为了更普遍地达到这一效果，有必要诉诸动态对冲策略。也就是说，我们将创建一个投资组合，但随后我们将不断需要向其中添加某些内容或在其中进行更改，以使到期时的付款完全符合我们的期望。

这是看涨期权飙升的有趣比例。尽管数学非常简单，但是在他的示例中，您可以看到在更复杂的情况下可以应用的几个非常重要的想法-无套利条件的应用，付款的重复和风险对冲。这是我们完成此简单关系的地方，可以继续构建更复杂的模型。

我们想建立一个模型，该模型不仅给出看涨期权和看跌期权之间的比率，而且给出期权价格作为市场上观察到的价值的函数。这将需要更复杂的数学理论。

什么是布朗运动，谁是罗伯特·布朗。如何在计算机上模拟布朗运动。什么是几何布朗运动

到目前为止，我们所考虑的内容使我们能够使用非常简单的数学仪器（实际上是学校数学）来解决问题。要继续建立更复杂的数学模型，这对我们来说还远远不够，因此需要“成人”数学元素。因此，进一步介绍的一般方法如下所示：我将给出说明性示例，从中可以清楚地了解数学仪器在简单情况下的工作方式，并且还将给出我们将使用的公式和定理。我不会证明这些定理。对数学部分感兴趣的人可以参考相应的教科书和视频课程。

我们需要的第一个概念是布朗运动...让我们记住这个术语在物理学中的含义。这将是在我们的正式数学模型中如何安排此过程的清晰示例。

我认为许多人使用“布朗运动”一词与学校物理课程相关联。许多人认为，将这个概念引入科学循环的人是物理学家，名字叫布朗，从名字上看，是英国人。有趣的是，所有这些假设都是错误的。首先，这位科学家的名字叫罗伯特·布朗，在俄文中应读作“罗伯特·布朗”。尽管对于18至19世纪受过教育的人来说，这可能并不明显，他们的第一外语是法语，而第二外语是德语。其次，他不是英国人-他是苏格兰人，据我们了解，这根本不是一回事。但最有趣的是，他不是物理学家-他是植物学家。当他进行并描述他著名的实验时，他正在显微镜下研究花粉颗粒。载玻片上的标本以液滴的形式制备，其中放置了花粉颗粒，以便这样花粉不会飞离所有草稿，并且可以从容观看。

布朗的注意力吸引到了他在显微镜目镜中看到的不是静止图像的事实。相对而言，他观察到一个圆形粒子引起了混沌运动。今天我们知道这种现象有一个简单的解释。该粒子周围的溶液中有许多分子，它们通常以随机方向与之相互作用，因此粒子会进行某种复杂的运动。

如果我们描述它的运动，它将是一些随机的轨迹。

这与我们的学科领域有什么关系？实际上，类推很简单。我们考虑一段时间内金融资产的利率。在每个时刻，以及该粒子上都有许多随机因素起作用。我们没有看到它们，就像罗伯特·布朗没有通过显微镜看到单个分子一样。

这些随机因素的累积效应导致资产过程的变化-就像分子的累积效应导致花粉颗粒的置换一样。这些过程会持续不断地发生。这样就实现了金融资产的利率。该过程对时间的依赖性是随机获得的，因此这种轨迹称为布朗运动。在我们的情况下，这是一维布朗运动，因为随机偏差仅围绕一个轴发生。

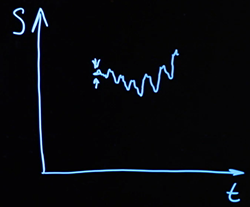
我们将使用的过程的正式数学模型与另一位科学家，美国数学家诺伯特·维纳（Norbert Wiener）的名字有关。看起来像这样。我们正在考虑一个连续的时间函数。因为

t

$t$ 是连续的，则函数

W (t)

$W(t)$ 连续。

它包含一个随机成分，该成分在数学上如下确定：

△ W_{△ t}

$\triangle W_{\triangle t}$ -独立的，前提是时间增量不相交。

从时间点开始的功能增量

t

$t$ 直到那一刻

t + s

$t+s$ 正态分布参数0和

s

$s$ （时间间隔的长度）。

W_{t + s} - W_{t} \sim N (0, s)

$W_{t+s}-W_t∼N(0,s)$

在下面的内容中，我们将看到能够在计算机上生成此类路径非常重要-这对于许多计算方法而言都是必需的。我们该怎么做？时间在理论数学模型中是连续的，我们在计算机上将其划分为一定的增量，通常以固定的步长进行。我们创建一个特定的起点，从该起点开始，我们的过程会带有坐标

W_{0}; t_{0}

$W_0;t_0$ ... 然后，对于随后的每个时间步，我们都会生成具有这种分布的随机变量，并将其移动一个步。我们在任何时候都这样做。结果是折线。

某个地方的增量结果带有一个加号，某个地方的结果带有一个负号。结果，在每个特定点，整个过程的值由所有这些随机变量的累加和确定。为了能够确定每单位时间的平均位移，我们还可以引入一个附加参数，通常用字母表示

σ

$\sigma$ （正态分布）。我们可以考虑功能

σ W_{t}

$\sigma W_t$ 哪里

W_{t}

$W_t$ 是标准的布朗运动，并且

W_{t}

$W_t$ 根据我们的需求，差异更大或更窄。

有了这样一个过程，我们想建立一个数学模型来帮助我们计算期权的价格。让我们根据与我们感兴趣的连续时间相同的原理构造方程。这将是某种微分方程。

如果我们要解决一定数量的利息问题

P

$P$ 在连续的时间内，那么一小段时间，我们就会有正确的关系

△ P = r P △ t

$\triangle P=rP\triangle t$ 要么

\frac{△ P}{P} = r △ t

$\frac{\triangle P}{P}=r\triangle t$ ，

在哪里

r

$r$ 是风险中性利率。并达到极限

Δ t \to d_{t}

$Δt →d_t$ ，我们得到了微分方程

\frac{d P}{P} = r d t

$\frac{dP}{P}=rdt$ ...

从中我们得到了连续时间打折的已经熟悉的公式

P = P_{0} e^{r t}

$P=P_0e^{rt}$ 哪里

P_{0}

$P_0$ 是初始值。

我想将这种推理逻辑应用于资产的数学模型，该资产的价格将来取决于随机因素。我们资产价格的相对变化由某个参数来表征，该参数类似于风险中立利率（在这种情况下，该参数表征了我们的基础资产，它不是风险中立利率）。让我们在该表达式中添加一个概率分量，该分量可以用布朗运动来描述。

\frac{Δ S}{S} = μ Δ t + σ Δ W

$\frac{ΔS}{S}=μΔt+σΔW$

我们实际上得到了结果。让我们移到极限，得到一个非常类似于我们容易解决的连续时间折扣的方程。

\frac{d S}{S} = μ d t + σ d W

$\frac{dS}{S}=μdt+σdW$

但是有一个技术问题。关键是，正如我们定义的那样，布朗运动（维纳过程）是时间的连续函数，但在经典数学分析的意义上是不可区分的。这可以被正式证明（我们省略了证明）。

为了在数学上严格构建这样的模型，有必要确定我们将表达式赋予什么含义

d W

$dW$ ... 为此，必须使用随机微分，其名称与另一位数学家的名称-Ito微分相关。它遵循的规则与我们在常规演算中习惯的规则不同。

作为参考，我将编写有关此数学仪器所需的结果。伊藤差速器遵守这些规则。

如果

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ ，

然后

f (x, t)

$f(x,t)$ ：

d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial x} d x + \frac{1}{2} \frac{\partial^{2} f}{\partial x^{2}} d x^{2}

$df=\frac{∂f}{∂t}dt+\frac{∂f}{∂x}dx+\frac{1}{2}\frac{∂^2f}{∂x^2}dx^2$ ...

该规则不同于我们在常规演算中区分两个变量的函数的方式。如果我们有两个自变量，则在普通演算中，我们将采用偏导数，并在扩展的前两个项处停止。伊藤公式中一个函数的微分展开的第三部分之所以出现，正是因为我们不是在使用普通函数，而是在随机地进行随机过程。我们将这个结果准备就绪，无需证明。

还有更多要说的

d x^{2}

$dx^2$ 在最后一个方程式中。根据条件

d x = a (x, t) d t + b (x, t) d W_{t}

$dx=a(x,t)dt+b(x,t)dW_t$ ，如果我们平方它，那么将有条件的条件

d t d W_{t}

$dt dW_t$ ，

d t^{2}

$dt^2$ ，

d W_{t}^{2}

$dW^2_t$ ... 要应用伊藤公式，您需要采取以下措施：

d t d W_{t} = 0

$dt dW_t=0$ ;

d t^{2} = 0

$dt^2=0$ ;

d W_{t}^{2} = d t

$dW^2_t=dt$ ...

如果您了解了Ito积分，那么所有这些规则都会很自然，但是就我们的目的而言，现在知道如何正确应用Ito公式就足够了。

现在我们可以克服技术上的复杂性，因为我们知道如何使用对象进行操作

σ d W

$σdW$ ...

作为变量

x

$x$ 我们有基础资产利率

S

$S$ ，我们可以表达它：

d S = S μ d t + σ S d W_{t}

$dS=Sμdt+σSdW_t$ ...

接下来，我们知道如何写函数的微分

S

$S$ 和

t

$t$ ... 让我们看看函数的区别是什么

f (S, t) = l n (S)

$f(S, t)=ln⁡(S)$ ...

d l n S = d f = \frac{\partial f}{\partial t} d t + \frac{\partial f}{\partial S} d S + \frac{1}{2} \frac{d^{2} f}{d S^{2}} d S^{2} =

$dln S = df = \frac{∂f}{∂t}dt+\frac{∂f}{∂S}dS+\frac{1}{2}\frac{d^2f}{dS^2}dS^2=$

= 0 d t + \frac{1}{S} (S μ d t + σ S d W_{t}) - \frac{1}{2} \frac{1}{S^{2}} σ^{2} S^{2} d t

$=0 dt+\frac{1}{S}(Sμdt+σSdW_t)-\frac{1}{2}\frac{1}{S^2}\sigma^2 S^2 dt$

现在，收集条件，我们得到对数的表达式

S

$S$ ...

d ㏑ S = (μ - \frac{σ^{2}}{2}) d t + σ d W

$d㏑S=(μ-\frac{\sigma^2}{2})dt+σdW$

现在我们知道什么等于

㏑ S

$㏑S$ （请注意，它具有正态分布）。我们直接对以下表达式感兴趣

S

$S$ ...

S = S_{0} e^{μ t} e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$S=S_0 e^{μt}exp(σW_t-\frac{\sigma^2}{2}t)$

上面的表达式描述了几何布朗运动。它代表着参数的指数增长

μ

$\mu$ 最初从点开始

S_{0}

$S_0$ ，根据表达式，噪声围绕该指数叠加

e x p (σ W_{t} - \frac{σ^{2}}{2} t)

$exp(\sigma W_t-\frac{\sigma^2}{2}t)$ ... 这已经可以在计算机上读取，我们可以生成布朗运动的路径。我们将获得一些潜在资产汇率的可能实现。该方程式有两个参数：

σ

$\sigma$ -方差和

μ

$\mu$ -漂移。它们对应于正态分布的方差和正态分布的偏差

㏑ S

$㏑S$ ... 正如我所说，现在可以在计算机上进行仿真，但是我们需要引入一个理论上的更多内容，以便可以使用此过程计算期权的价格。接下来，我们将讨论风险中性措施。

本系列的所有文章

选项：挂断电话，布朗移动。极客教育计划，第7部分

挂断电话。使用无套利条件分析工具组合价格的示例

什么是布朗运动，谁是罗伯特·布朗。如何在计算机上模拟布朗运动。什么是几何布朗运动

More articles: