🗑️ 🌎 👨‍👩‍👦 里德-所罗门码 🧘🏻 👩🏼‍🎓 👩🏾‍💻

在通信系统和计算机的通道中处理编码消息的信息流时，密码学的一项重要任务是流的分离以及根据给定功能对其进行选择。专用流被分成单独的消息，并对每个消息进行深入分析，以建立代码及其特征，然后进行解码和访问消息的语义。

因此，例如，对于某些里德-所罗门代码（PC代码），您需要设置：

码字（块）的长度n；
k个信息和Nk个校验符号的数量；
定义有限域GF（2 ^r）的不可约多项式p（x ）；
有限域的本原元素α；
生成多项式g（x）;
代码的参数j；
使用交错
码字或符号向信道和其他信道的传输顺序。

这里，在工作中考虑了一个稍有不同的特定问题-PC代码本身的建模，这是上述代码分析问题的主要部分。

PC代码及其特性的描述

为了方便起见并更好地理解PC代码设备的本质和编码过程，我们首先介绍代码的基本概念和术语（元素）。

里德-所罗门码（RS码）可以解释为非二进制BCH码（Bose-Chowdhury-Hawkingham），其代码符号的值取自GF（2 ^r）字段，即r信息符号显示为该字段的单独元素。 Reed-Solomon码是线性非二进制系统循环码，其符号是r位序列，其中r是大于1的正整数。

在所有n和n的r位符号上定义了Reed-Solomon码（n，k）。 k，其中：

0 <k <n <2 ^r + 2，其中

k是要编码的信息符号的数量，

n是编码块中的代码符号的数量。

对于大多数（n，k）Reed-Solomon码；（N，K）=（2 ^{- [R} -1，2 ^{- [R} -1-2∙t），其中

t是该代码可以校正的错误符号的数量，以及

N - K = 2T为校验符号的数目。

Reed-Solomon码具有线性码可能的最大最小距离（区分序列的字符数）。对于里德-所罗门码，最小距离定义如下：dmin = n – k +1。

定义。在域GF PC码（Q =^米），与块长度n = Q^米纠正t错误的-1是GF（q）上所有码字u _（n）的集合，其中2t个连续频谱分量带有数字

m_{0}, m_{0} + 1, . . ., m_{0} + 2 t - 1

$m_0,m_0 +1,...,m_0+2t-1$ 等于

0。2的连续α幂是生成多项式g（x）的根或频谱包含

连续零分量的事实是该代码的重要属性，它可以校正t误差。

信息多项式Q。指定消息的文本，该文本分为恒定长度的块（单词）并被数字化。这就是要在通信系统中传输的内容。

生成多项式PC代码的g（x）是通过将Q·g（x）== u _（n）乘以GF（q）将信息多项式（消息）转换成代码字的多项式。

校验多项式h（x）使您可以确定单词中是否存在变形的字符。

多项式多项式S（z）。一个包含与错误位置相对应的分量的多项式。针对解码器接收到的每个单词进行计算。

误差多项式E.长度等于代码字的多项式，除包含代码字符号失真的位置外，所有位置的值均为零。

错误定位器多项式Λ（z）提供根，表示由通信信道（解码器）的接收端接收到的单词中的错误的位置。可以通过反复试验找到其根源，即通过依次替换该字段的所有元素，直到Λ（z）等于零。

误差值Ω（z）≡Λ（z）·S（z）（modz ^2t）的多项式的模数z ^2t与误差定位器多项式乘以该多项式的乘积可比。

字段p（x）的不可约多项式。有限字段不存在任何数量的元素，仅当元素的数量是素数p或q = p ^m的幂时才存在质数。在第一种情况下，该字段称为简单字段（它的元素是对质数为p的数的残差），在第二种情况下，它是相应简单字段的扩展（其阶数为m-1或以下的多项式的q个元素是对多项式p进行模数的多项式的残差（x）

阶m）本原多项式。如果该字段的不可约多项式的根是本原元素α，则p（x）被称为不可约本原多项式。

在用PC代码描述动作的过程中，我们将需要重复引用Galois字段，因此在此我们将立即放置一个包含该字段的元素的工作表，并用不同的元素表示形式（小数，二进制矢量，多项式，原始元素的次数））。

表II-扩展GF（2 ⁴），不可约多项式p（x）= x ⁴ + x + 1，的有限域元素的特征，基本元素α= 0010 = 2 ₁₀

例子1。在有限域GF（2 ⁴）上，给出了不可约域多项式p（x）= x ⁴ + x +1，给出了原始元素α= 2，并给出了（n，k）-Reed-Solomon码（PC码）。该代码的代码距离为d = n-k + 1 =7。此代码最多可以纠正消息块（代码字）中的三个错误。

该代码的生成多项式g（z）的阶数为m = nk = 15-9 = 6（其根是字段GF（2 ⁴）的6个元素（以十进制表示），即元素2、3、4、5、6、7）和由比率决定，即 z的多项式，系数（元素）来自GF（2 ⁴），以i = 1（1）6的十进制表示。在考虑的PC代码中，2 ⁹ = 512个码字。

PC消息编码

在表II中，这些根也具有幂表示

α^{1} = 2, α^{2} = 3, . . ., α^{6} = 7

$α^1=2, α^2=3,...,α^6=7$ ...

这里z是一个抽象变量，而α是该字段的原始元素，通过其幂表示该字段的所有（16）个元素。字段元素的多项式表示使用x变量。

PC代码的生成多项式g（x）= A B的计算分部分进行（每个过程用三个括号括起来）：

生成多项式的向量表示形式（根据字段元素以十进制表示形式表示的系数g（z））为

g（z）= G ₇ =（1、11、15、5、7、10、7）。

在生成面向错误检测和纠正的PC代码的生成多项式之后，设置一条消息。该消息以数字形式（例如ASCII码）呈现，从该形式过渡到多项式或矢量表示。

信息向量（消息词）具有k-来自（n，k）的分量。在示例k = 9中，向量是9分量，所有分量都是GF字段（2 ⁴）的元素，以十进制表示形式Q _<9> =（11，13，9，6，6，7，15，14，12，10） ...

根据该向量，形成代码字u_<15>是具有15个分量的向量。像代码本身一样，代码字是系统的和非系统的。通过将信息向量Q乘以与生成多项式相对应的向量来获得非系统码字

转换后，我们以

Q·g = <11、15、3、9、6、14、7、5、12、15、14、3、3、7、1>的形式获得非系统代码字（向量）。

在系统编码中，消息（信息矢量）由多项式Q（z）表示，形式为Q（z）= q（z）g（z）+ R（z），其中degR（z）<m = 6。右边的向量Q被分配了余数R（全部为十进制形式）。这样做是这样的。

多项式Q朝着较高的数字移位m = n-k，这是通过将Q（z）乘以Z ^n-k（在示例中Z ^n-k = Z ⁶）获得的，并且在移位之后，除法Q（z）Z ^n-k x（z）。结果，找到除法R（z）的余数。所有操作都在GF字段上执行（2 ⁴）

（11、13、9、6、7、15、14、12、10、0、0、0、0、0、0）=

=（1、11、15、5、7、10、7）（ 11、15、9、10、12、10、10、10、10,3）+（1、2、3、7、13、9）= G·S +R

。多项式除法的余数以通常的方式计算（请参见角这里是示例6）。根据以下模式执行除法：设Q = 26，g（z）= 7，然后26 = 7 3 + R（z），R（z）= 26 -7 3 = 26-21 =5。计算余数R（z ）关于多项式的除法。我们将剩余的R赋给右边的向量Q，

得到u _<15> -一个系统形式的代码字。该视图清楚地在代码字

u _<15> =（11,13,9,6,7,15,14,12,10; 1，2，3，7，13，9）的k个高阶位中包含一条信息消息

向量的数字从0（1）14从右到左编号。右边的六个最低有效位是校验位。

解码里德-所罗门码

接收到一个块后，解码器将处理每个块（代码字）并纠正在传输或存储过程中发生的错误。解码器将所得多项式除以RS码的生成多项式。如果余数为零，则未发现错误，否则将发生错误。

典型的PC解码器在解码循环中执行五个步骤，即：

计算多项式多项式（其系数），发现误差。
解决了关键的Pade方程-计算误差值及其在相应位置的位置。
执行Chen的过程-查找错误定位器多项式的根。
Forney算法用于计算误差值。
纠正了失真的代码字；

通过从代码字中提取消息（删除代码）来结束循环。

综合症的计算。

从接收到的码字生成综合症是

解码过程的第一步。在此计算校正子并确定接收到的码字中是否有错误，

可以以不同的方式组织PC码字的解码。经典方法包括使用在时域或频域中操作的算法进行解码，该算法要么使用校正子的计算，要么不使用校正子的计算。在不深入研究这个问题的理论的情况下，我们将选择在时域中通过码字校正子的计算进行解码。

失真检测

综合症

S = (S_{v}, S_{v + 1}, . . ., S_{m + v - 1})

$S = (S_v,S_{v+1},...,S_{m+v-1})$ 哪里

v ∊ 0, 1

$v∊{0, 1}$ 对于解码器在其输入处接收到的每个码字，顺序确定矢量。校正子向量的成分为零值

S j = 0, j = v, v + 1, . . ., m + v - 1

$Sj = 0, j=v,v+1,...,m + v - 1$ 因此，解码器认为接收到的字没有错误。如果至少有一个

j \geq 1, S j \neq 0

$j≥1,Sj≠0$ ，则解码器得出结论，认为代码矢量中存在错误，并继续进行识别，这是解码器操作的第一步。通过奇偶校验矩阵H在代码字C的接收端

计算多项式多项式

乘积可得出两个结果：

校正子向量S = 0，对应于向量C中没有错误；
校正子向量S≠0，这表示向量C的成分中存在错误（一个或多个）。

第二种情况很有趣。

带有错误的代码向量表示为C（E）= C + E，E是错误向量。然后

(C + E) H^{t} = C H^{t} + E H^{t} = 0 + E H^{t} = S

$(C +E)H^t = CH^t + EH^t = 0 + EH^t = S$

证候的分量Sj由

n = q-1和j = 1（1）m = nk的求和关系确定，或由Horner方案确定：

S_{j} = C_{0} + α^{j} (C_{1} + α^{j} (C_{2} + . . . + α^{j} (C_{n - 2} + α^{j} C_{n - 1}) . . .))

$S_j = C_0 +α^j(C_1 +α^j(C_2 +...+α^j(C_{n-2} +α^jC_{n-1})...))$

例子2。令误差向量的形式为= <0 0 0 0 12 0 0 0 0 0 0 0 0 0 0 0 0>。它会在代码向量的第3位和第10位处破坏字符。错误值分别为8和12-这些值也是GF字段（2 ⁴）的元素，并以十进制（表P）表示法给出。在向量E中，从0（1）14开始，位置从右到左从低位开始编号。

现在让我们形成一个代码向量，该向量在第3位和第10位有两个错误，分别具有值8和12。这是通过在GF（2 ⁴），请按照该字段的算术规则进行。字段元素的总和为零不会更改其值。非零值（字段元素）在将它们转换为多项式表示形式后进行求和，因为通常对多项式进行求和，但是未知数的系数被简化为mod 2.

获得求和结果后，它们再次转换为十进制表示形式，之前已通过幂表示

下图显示了在码字的10和3位置处的错误损坏值的计算：

(7 + 12) \to α^{6} + α^{1} 1 = x^{3} + x^{2} + x^{3} + x^{2} + x^{1} = α^{1} = 2,

$(7+12) →α^6+α^11 =x^3 +x^2 +x^3 +x^2 +x^1 =α^1 = 2,$

(3 + 8) \to α^{2} + α^{7} = x^{2} + x^{3} + x^{1} + 1 = α^{12} = 13.

$(3 + 8) →α^2+ α^7 =x^2 +x^3 +x^1 + 1 =α^{12}=13.$

解码器根据通用公式对分量Sj，j = 1（1）m进行计算。这里（在模型中）我们使用关系

S = E H^{t}

$S=EH^t$ ，因为我们自己在程序中指定（模拟），所以仅当i = 3和i = 10时才获得非零项。

下面，我们将以展开形式特别显示此公式的计算。

PC的校验矩阵-代码

一旦公式化了代码的生成多项式，就可以构造用于代码字的奇偶校验矩阵，并确定要纠正的错误数（请参见此处的解码器）。让我们构造一个辅助矩阵[7×15]，从中可以获得两个不同的奇偶校验矩阵：前六行是一个，而后六行是另一个。

矩阵本身以特殊方式形成。前两行是显而易见的，第三行和所有后续行是通过从前一行（第二行）减去自然数为1、2、3、4、5、6、7、8、9、10、11、12、13、14的段而获得的15 mod15。当出现零值时，将其替换为15，将负残基转换为正残基。

每个矩阵对应于其自己的用于系统编码和非系统编码的生成多项式。

多项式系数的确定

接下来，我们将确定j = 1（1）6时的多项式系数。

关于具有长度的码字

n < q = p^{r}

$n<q=p^r$ 到达解码器的输入时，我们假设它已因错误而失真。

为了确定错误的向量，您需要了解以下内容：

代码字中变形位置的数量
$v≤v_{max}=0.5m$ ;
码字中变形位置的数量（位置） $ℓ_i: ℓ_i=0(1)n-1$ ;
失真值 $e_ℓ; e_ℓ∊GF(2^4)$ ...

校正子向量（多项式）S如何计算和使用？它在解码码字中的作用非常重要。让我们用一个数字示例来说明这一点。

例子3。（校正子向量的分量的计算

S_{< 6 >}

$S_{<6>}$ ）

最后，我们有

S_{< 6 >} = (S_{1}, S_{2}, S_{3}, S_{4}, S_{5}, S_{6})

$S_{<6>}=(S_1,S_2,S_3,S_4,S_5,S_6)$ = <8,13,7,13,15,15>

为进一步考虑，我们引入了新概念。价值

x_{i} = α^{ℓ_{i}}

$x_i = α^{ℓ_i}$ 将被称为错误定位器，此处的位置是变形的代码字符号

ℓ_{i}

$ℓ_i$ ，α是字段GF（2 ⁴）的原始元素。

下面将特定码字的错误定位符集合视为错误定位符多项式σ（z）的系数，根

z_{i}

$z_i$ 值是多少

x_{i}^{- 1}

$x_i ^{-1}$ 与定位器成反比。

此外，表达式

(1 - z x_{i}) = 0

$(1-zx_i)=0$ 消失。

σ (z) = (1 - z x_{1}) (1 - z x_{2}) . . . (1 - z x_{v}) = σ_{v} z^{v} + σ_{v - 1} z^{v - 1} + . . . + σ_{1} z + σ_{0}

$σ(z) = (1-zx_1)(1-zx_2)...(1-zx_v) =σ_vz^v +σ_{v-1}z^{v-1} +...+σ_1z +σ_0$

方程的总是自由项方程的总是自由项

σ_{0} = 1

$σ_0 =1$ ...

错误定位器的多项式的阶数等于v-错误的数量且不超过该值

v \leq v_{m a x} = 0.5 m

$v≤v_{max}=0.5m$ ...

因此，所有变形的字符在单词中的位置不同

x_{i} = α^{i}

$x_i = α^i$ ，不能有重复的字段元素，并且多项式σ（z）= 0没有多个根。

为了方便编写，错误值将用符号重新指定

Y_{i} = e_{i}

$Y_i = e_i$ ... 对于综合多项式的系数，以前考虑了非线性方程。在我们的案例中，v = 1是综合症成分的起源。

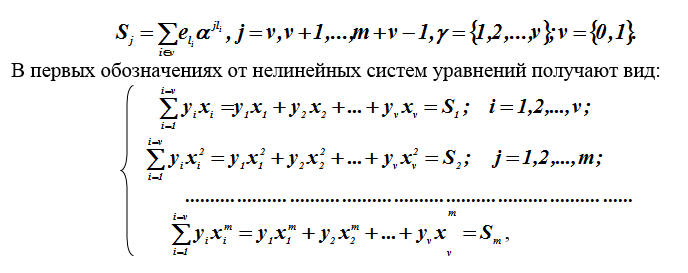
哪里

y_{i}, x_{i}

$y_i,x_i$ 是未知数量，并且

S_{j}

$S_j$ -在解码的第一阶段计算出的已知参数（校正子向量的分量）。

解决此类非线性方程组的方法尚不清楚，但可以使用技巧（变通方法）找到解决方案。对系数的线性方程式的Hankel（Toeplitz）系统进行了转换

σ_{i}

$σ_i$ 定位多项式。

转换为线性方程组转换为

方程

σ_{i}

$σ_i$ 错误定位多项式的值，其根的值被替换

z = x_{i}^{- 1}

$z =x_i^{-1}$ ... 在这种情况下，多项式消失。形成一个恒等式，其两边乘以

y_{i} x_{i}^{j + v}

$y_ix_i^{j+v}$ ，我们得到：

y_{i} (σ_{v} x_{i}^{j} + σ_{v - 1} x_{i}^{j + 1} + . . . + σ_{1} x_{i}^{j + v - 1} + x_{i}^{j + v}) = 0, 1 \leq i \leq v, 1 \leq j \leq v

$y_i(σ_vx_i^{j}+σ_{v-1}x_i^{j+1}+...+σ_1x_i^{j+v-1}+x_i^{j+v})=0,1≤i≤v, 1≤j≤v$ ...

我们获得了平等

v \times v = v^{2}

$v×v =v^2$

我们总结了所有这些平等

i, 1 \leq i \leq v

$i, 1≤i≤v$ 为此，这些平等都得到了满足。由于多项式σ（z）具有v根

x_{i}^{- 1}

$x_i^{-1}$ ，打开括号并传递系数

σ_{i}

$σ_i$ 每个金额的符号：

在此等式中，根据

之前给出的非线性方程组，每个和都等于校正子向量的分量之一。因此他得出结论，关于系数

σ_{v}, σ_{v - 1}, . . ., σ_{1}

$σ_v, σ_{v-1},...,σ_1$ 您可以写出线性方程组。

在二进制字段上进行计算时，省略了符号“-”，因为它们对应于“ +”。线性方程组的最终结果是汉克尔，并且对应于一个具有维数的矩阵

v \times (v + 1)

$v×(v+1)$ 一点。

如果码字C（E）中的错误数严格等于

v, v \leq 0.5 (n - k)

$v , v ≤0.5(n-k)$ ，即不违反该代码的抗噪能力。

求解线性方程组

所得线性方程组包含作为未知数的系数

σ_{i} = 1 (1) t

$σ_i =1(1)t$ 码字C（E）的错误定位符多项式。症状向量的先前计算出的分量被认为是已知的

S_{j}, j = 1 (1) m

$S_j, j=1(1)m$ ... 这里，t是单词中的错误数，m是单词中的校验位置数。

有多种方法可以解决已形成的系统。

注意（Hankel）矩阵不会因单个单词允许的错误数（小于0.5m）而受到限制。在这种情况下，方程组得到了唯一的求解，问题可以简单地归结为汉克尔矩阵的求逆。消除对矩阵尺寸的限制是合乎需要的。在无尽的领域。

在无限域上，求解Hankel线性方程组的方法是已知的：

迭代Trench-Berlekamp-Messi方法（TBM方法）；（1）
直接确定性的Peterson-Gorenstein-Zierler；（PHC-方法）; （2）
使用Euclid算法的Sugiyama方法找到GCD（C方法）。（3）

在不考虑其他方法的情况下，我们将选择TBM方法。选择的动机如下。

该方法（PHC）简单而又好，但是对于少量可纠正的错误，C方法很难在计算机上实现，并且在来源中受到限制地发布（覆盖），尽管C方法类似于根据校正子S（z）的多项式的TBM方法提供了Galois场上Pade方程的解。该方程式是针对误差定位符σ（z）和多项式ω（z）的多项式而形成的，在编码理论中，它称为关键Pade方程：

S (z) σ (z) = ω (z) (m o d z^{m})

$S(z)σ(z) = ω(z)(mod z^m)$ ...

关键方程的解是集合

x_{i}^{- 1}

$x_i^{-1}$ 多项式σ（z）的根，以及相应的定位符

x_{i} = α^{ℓ_{i}}

$x_i =α^{ℓ_i}$ ，即错误位置。误差值（幅度）

e_{i}

$e_i$ 由Forney公式以以下形式确定

哪里

σ_{z}^{^{'}} (α^{- i})

$σ_z^{'}(α^{-i})$ 和

ω (α^{- i})

$ω(α^{-i})$ 是该点的多项式σ（z）和ω（z）的值

z = α^{- i}

$z =α^{-i}$ 与多项式σ（z）的根相反；

我是错误的位置；

σ_{z}^{^{'}} (z)

$σ_z^{'}(z)$ -多项式σ（z）相对于z的形式导数；

有限域中多项式的形式导数

关于实数领域中的变量和有限领域中的形式导数，导数存在差异和相似之处。考虑多项式

a_{i}

$a_i$ 是字段元素，i = 1（1）n个

字段元素。给出了实场GF（2 ⁴）上的代码。关于z的导数为：

在一个无限的实场中，这些运算乘以n并求和n次。对于有限域，导数定义不同。

导数类似地由比率确定：

其中（（i））= 1 +1 + ... + 1（i）次，根据有限域的规则求和：+号表示“累加很多次”的运算，即元件

a_{2} z

$a_2z$ 重复2次，元素

a_{3} z^{2}

$a_3z^2$ 重复3次，元素

a_{n} z^{n - 1}

$a_nz^{n-1}$ 重复n次。

显然，该运算与有限域中的乘法运算不符。尤其是在字段GF（2 ^r）中，mod2取偶数个相同项的总和并置零，并且奇数等于项本身不变。因此，在字段GF（2 ^r）中，导数采用以下形式

此字段中的第二和最高偶数导数等于零。

从代数可知，如果一个多项式具有多个根（多重性p），则该多项式的导数将具有相同的根，但具有多重性p-1。如果p = 1，则f（z）和f'（z）没有共同根。因此，如果多项式及其导数具有一个公因数，则存在多个根。导数f'（z）的所有根都是f（z）的倍数。

关键方程解法

TMB（Trench-Berlekampa-Messi）是一种求解关键方程的方法。迭代算法提供了多项式σ（z）和ω（z）的定义，以及Pade（key）方程的解。

初始数据：多项式系数

S_{1}, S_{2}, . . ., S_{n}

$S_1,S_2,...,S_n$ n-1级。

目标。以显式（解析）形式定义多项式σ（z）和ω（z）。

该算法使用以下符号：j-步骤号，

v_{j}

$v_j$ -多项式的次数，

σ_{j} (z) = σ_{j i} z^{i} + σ_{j i - 1} z^{i - 1} + . . . + σ_{j 1} z + σ_{j 0}

$σ_j(z) =σ_{ji}z^i +σ_{ji-1}z^{i-1}+...+σ_{j1}z+σ_{j0}$ -多项式的幂次展开

z, k_{j}, L_{j}, θ_{j} (z)

$z, k_j, L_j, θ_j(z)$ 和

Ω_{j} (z)

$Ω_j(z)$ -算法第j步的中间变量和函数；

必须指定初始条件，因为此处使用了递归。

初始条件：

例子4。向量

S =（8,13,7,13,15,15）的迭代算法的执行。定义多项式

σ (z) = σ_{n} (z)

$σ(z) =σ_n(z)$ 和

ω (z) = ω_{n} (z)

$ω(z) = ω_n(z)$ ...

表2-错误定位器多项式的计算

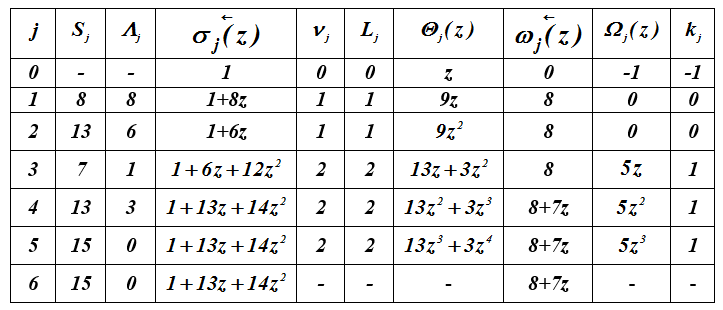
所以

σ_{j}^{\leftarrow} (z) = 14 z^{2} + 13 z + 1

$σ_j^←(z)=14z^2+13z+1$ ，

ω_{j}^{\leftarrow} (z)

$ω_j^←(z)$ = 7z + 8。具有不可约多项式p（x）= x ⁴ + x + 1

的场GF（2 ⁴）上的误差定位多项式σ（z）具有根

z_{1} = α^{- i_{1}} = 13 = 4^{- 1}

$z_1 = α^{-i_1} = 13 = 4^{-1}$ 和

z_{2} = α^{- i_{2}} = 6 = 11^{- 1}

$z_2 =α^{-i_2} = 6 = 11^{-1}$ ，很容易通过直接验证来进行验证，即

i_{1} = 3, i_{2} = 10, 13 = α^{12}, 1 = α^{12} α^{3}

$i_1= 3, i_2 =10, 13 = α^{12}, 1 =α^{12}α^{3}$ 和

α^{12} = α^{- 3} => 13 = 4^{- 1}

$α^{12} =α^{-3}=>13=4^{-1}$ ... 根替换

σ (z = 13) = 14 (13)^{2} + 13 \cdot 13 + 1 = α^{13} (α^{12})^{2} + (α^{12})^{2} + α^{0} = α^{37} + α^{24} + α^{0}

$σ(z=13)=14(13)^2+13·13+1=α^{13}(α^{12})^2+(α^{12})^2+α^0= α^{37}+α^{24} +α^{0}$ =

=

α^{7} + α^{9} + α^{0} = x^{3} + x + 1 = 0 (m o d 2)

$α^{7}+α^{9}+α^0 =x^3+x+1=0(mod2)$ ;

σ (z = 6) = 14 (6)^{2} + 13 \cdot 6 + 1 = α^{13} (α^{5})^{2} + (α^{5})^{2} + α^{0}

$σ(z = 6)=14(6)^2+13·6+1 = α^{13}(α^{5})^2+(α^{5})^2+α^{0}$ =

=

α^{8} + α^{2} + α^{0} = x^{2} + 1 + x^{2} + 1 = 0 (m o d 2)

$α^{8}+α^{2} +α^{0} = x^2 +1+x^2 +1 = 0(mod2)$ ...

取σ（z）的形式导数，我们得出σ_2（z）= 2 14 + 13 = 13，这是因为14z被取和为2倍并且消失了mod 2。

使用Forney公式，我们将找到用于计算误差值的表达式

e_{i}

$e_i$ ...

在最后一个表达式中替换值i = 3和i = 10位置，

我们发现

е_{3} = 10 α^{15 - 3} + 11 = α^{6} + α^{10}

$_3 = 10α^{15-3}+11 =α^{6}+α^{10}$ = =

x^{3} + x^{2} + x^{2} + x + 1 = x^{3} + x + 1 = α^{7} => 8

$x^3+x^2+x^2+x+1=x^3+x+1=α^{7}=>8$ ;

е_{10} = 10 α^{15 - 10} + 11 = α^{9} α^{5} + α^{10} = α^{14} + α^{10}

$_{10} = 10α^{15-10}+11 =α^{9}α^{5}+α^{10}=α^{14}+α^{10}$ = =

x^{3} + x^{2} + x = α^{11} => 12

$x^3+x^2+x=α^{11}=>12$ ...

构建软件包的架构

为了构建软件包，建议使用以下体系结构解决方案。该软件包被实现为具有图形用户界面的应用程序。

软件包的初始数据是使用文件中的转储卸载的数字信息流。为了便于分析和简化复杂操作，建议使用.txt文件。

在执行各种计算动作的复杂工作过程中，以数据数组的形式显示已加载的数字流。

在复杂操作的每个阶段，都可以可视化工作的中间结果。

程序复杂运算的结果以表格中显示的数字数据的形式显示。

中间和最终分析结果将保存到文件中。

复杂软件的功能方案

使用复杂软件的操作开始于使用文件转储来加载数字流。下载后，将为用户提供文件二进制内容及其文本内容的可视表示。

在此接口的框架内，应执行以下功能任务：

下载原始消息；
将消息转换为转储；
消息编码；
模拟截获的消息
构造接收代码字的频谱，以分析它们的视觉表示；
显示代码参数。

软件包操作说明

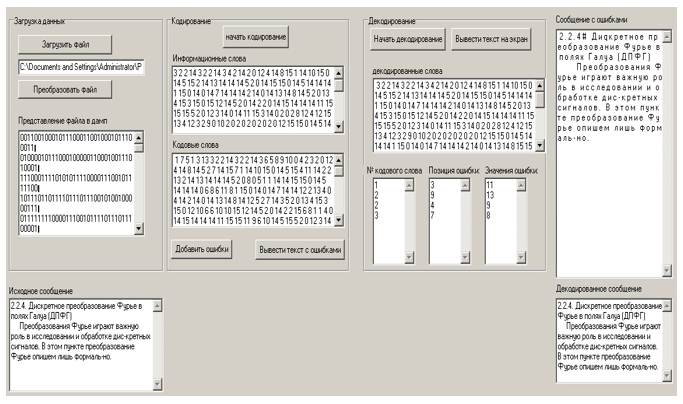
启动程序的可执行文件时，屏幕上将显示图2所示的窗口，其中显示了程序的主界面。

程序的输入是一个文件，需要通过通信通道进行传输。对于其在真实通信信道上的传输，需要进行编码-向其添加校验符号，这对于在源-接收器中对单词进行明确解码是必需的。要启动综合系统，您需要使用“加载文件”按钮选择所需的文本文件。其内容将显示在主程序窗口的下部字段中。

消息的二进制表示形式将显示在相应字段中，即信息字的二进制表示形式-在“信息字的二进制表示形式”字段中。

原始消息中的位数和其中的单词总数显示在“已发送消息中的位数”和“已发送消息中的单词数”字段中。

形成的信息和代码字显示在主程序窗口右侧的表中。

具有中间结果的程序窗口如图3所示。

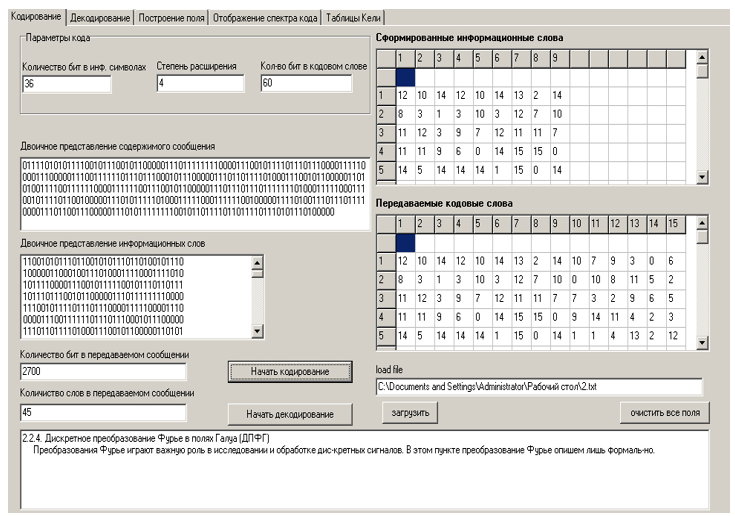
图3-软件包结果的中间表示

图4.下载消息文件的结果

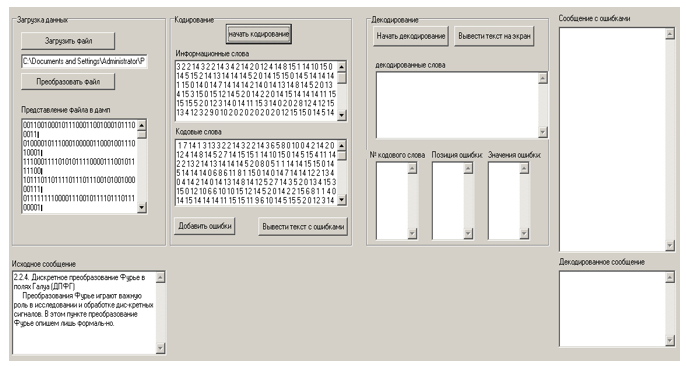
图5.文件编码结果

图6.带有错误输入的消息输出。

图7.解码结果和引入错误

的消息的输出图8.解码消息的输出。

结论

美国国家安全局是埃施朗全球拦截系统的主要运营商。梯队拥有广泛的基础设施，包括遍布全球的地面跟踪站。几乎所有世界信息流都受到监视。

对当前在技术和政治领域中主动信息战中获取已编码信息消息的语义的可能性进行研究的研究已成为另一挑战，也是当今时代的紧迫任务之一。

在绝大多数代码中，消息（信息）的编码和解码是在有限扩展Galois字段的严格数学基础上实现的。处理此类字段的元素不同于通常在算术中接受的元素，并且在使用计算工具时需要编写特殊的过程来操作字段元素。

提供给读者注意的工作在公司，公司和整个州的层面上稍微揭开了对此类活动的保密面纱。

参考书目

. , . – .: , 1986. – 576 .
- . , . . . , . – .: , 1979. – 744 .
. . – .: , 1971. – 478 .
.., .. . – .: , 1986. – 176 ., .
. . . – .: , 2004. – 288 .
.. . . – : - , 2005. – 147 .
. ., .. . – : , 2001. – 60 .
., ., ., . . – .: , 1978. – 576 .
. . . – .: . , 1990. – 288 .
. ., .. « »/ . .26. . .. –. .: .. , 2007. – . 121-130.
. ( 2. ). – . . . , 2002. – 97 .
. . . – .: , 1987 – 120 .

里德-所罗门码