通过将凯勒的假设翻译成计算机可理解的图形搜索语言,研究人员终于解决了用瓷砖覆盖空间的问题

一队数学家终于弄清楚了凯勒的假设-但不是靠自己。相反,他们培训了整个计算机团队,并解决了问题。
奥特·海因里希·凯勒(Ott-Heinrich Keller)90年前提出的凯勒假说与用相同的瓷砖覆盖空间的任务有关。她认为,如果您用二维正方形瓷砖铺砌一个二维空间,那么其中至少有两个必须完全而不是部分地接触边。该假设对任何尺寸都做出相同的预测-也就是说,当用12维“正方形”填充12维空间时,其中至少两个必须具有公共边。
多年以来,数学家一直在为这一假设而奋斗,在某些方面证明了它的真实性,而在另一些方面证明了它是错误的。到去年秋天,仅对七维空间这个问题仍未解决。
但是新的计算机生成的证据也解决了这个问题。该证明于去年10月发布,是人类天才和纯粹的计算能力相结合以回答数学中最令人兴奋的问题的最新示例之一。
这项新著作的作者是斯坦福大学的约书亚·布劳肯西克(Joshua Breukensik),卡内基梅隆大学的马林·希祖尔和约翰·麦基,以及罗彻斯特理工学院的戴维·纳尔维兹,他们使用40台计算机解决了这一问题。在短短30分钟内,这些机器产生了一个单音节答案:是的,在七个维度上,该假设是正确的。而且,我们甚至不必对信仰做出这个结论。
答案附带有很长的证据来解释其真相。该证明对于人类来说太长了,但是另一个计算机程序可以对其进行验证。
换句话说,即使我们不确切知道计算机是如何证明凯勒假说的,我们也至少可以确定他们做对了。
神秘的第七维度
不难发现,凯勒的猜想在两个维度上都是正确的。拿一张纸,并尝试以相等的正方形覆盖,没有缝隙或重叠。很快,您将意识到只有在至少两个正方形具有相同边的情况下才能执行此操作。如果手边有多维数据集,将很容易验证第三个维度的假设是正确的。 1930年,Keller建议这种关系适用于所有尺寸及其对应的图块。
早期结果支持凯勒的预测。 1940年,奥斯卡·佩隆(Oscar Perron)证明了这一假设对于测量一到六是正确的。然而,超过50年后,新一代数学家发现了该假设的第一个反例:1992年,杰弗里·拉加里亚斯(Jeffrey Lagarias)和彼得·肖尔(Peter Shore)证明该假设在第10维上不起作用。

凯勒的假设预测,当以任何尺寸填充空间时,至少有两个瓷砖必须完全接触侧面。
当填充二维空间时,许多瓷砖具有相同的边(蓝线)。
填充3D空间时,许多立方体都有公共面(蓝色)。
很容易证明,如果某个假设在某个维度上失败,那么它就不会在所有更高的假设中成立。因此,在拉加里亚斯和绍尔的工作之后,剩下的只是解决第七,第八和第九个方面的问题。在2002年,麦基(Mackey)证明了凯勒的假设对于第8维(因此也是第9维)是错误的。
只有第七维保持开放状态-它是该假设正确的最大维度,或者是该假设不正确的最小维度。
“没有人确切知道那里发生了什么,” Khiyul说。
将点连接
尽管数学家为这个问题奋斗了几十年,但他们的方法却逐渐改变。 Perron仅使用铅笔和纸来研究前六个维度,但是到1990年代,研究人员已经弄清楚了如何将Keller的假设转换为完全不同的形式-允许他们使用计算机来解决它。
凯勒猜想的原始表述涉及光滑的连续空间。在这样的空间中,有无数种放置无数瓷砖的方法。但是,计算机无能为力,无法解决无数选项的问题-要解决这些问题,它们需要离散且有限的对象。

卡内基梅隆大学的Marin Hijul
1990年,Kereszteli Korradi和Sandor Shabo提出了一个合适的离散对象。他们表明,可以就此对象提出与凯勒假说等同的问题。并且,如果您证明与这些物体有关的东西,那么凯勒假说将得到证明。这将无穷大的问题简化为具有多个数字的较不复杂的算术问题。
运作方式如下。
假设您要在两个维度上处理凯勒假说。 Corradi和Chabot提出了一种使用结构构造的方法,他们称之为Keller图。
首先,假设桌子上有16个骰子,并且每个骰子的上边缘都有两个点(两个点表示二维空间,以及为什么有16个立方体-我们稍后会看到)。所有多维数据集都以相同的方式旋转,因此每个人的两个点都位于同一位置。用四种颜色中的任何一种为每个点着色:红色,绿色,白色或黑色。
一个立方体上的点不会改变位置-让其中一个表示x坐标,另一个-y。多维数据集着色后,如果满足两个条件,我们就开始在成对的多维数据集之间绘制线条或边缘:一对多维数据集在同一位置的点具有不同的颜色,而在另一位置它们是不同的和成对的,则成对的点被视为红色与绿色或黑色与白色。
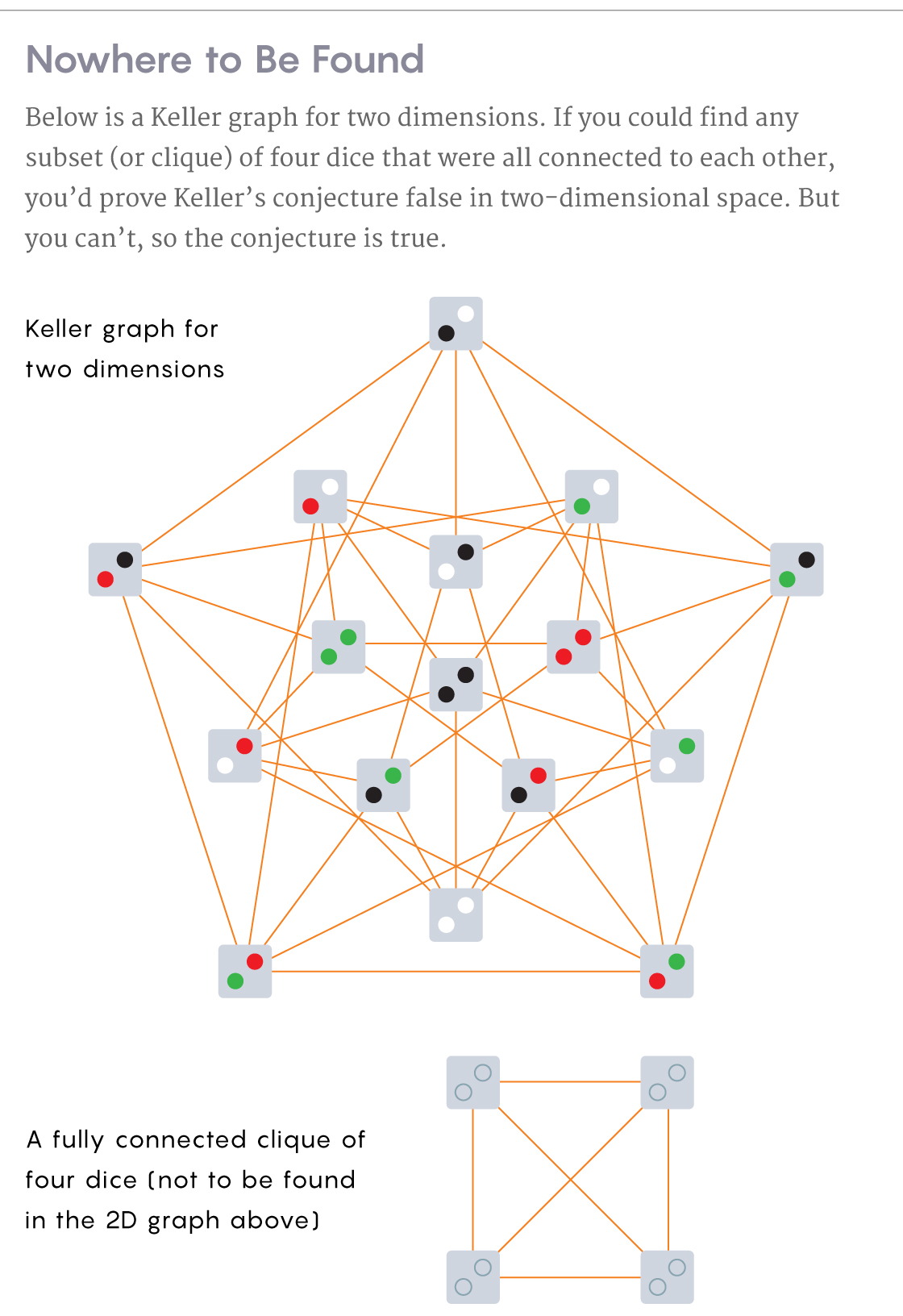
二维的凯勒图。找到四个多维数据集的一个子集,其中每个多维数据集都相互连接,您将证明二维空间的凯勒假设不成立。但是,没有这样的子集,并且该假设是正确的。
以下是图中未包含的四个骰子的完全合并集团的示例。
也就是说,例如,如果一个多维数据集具有两个红点,而另一个多维数据集具有两个黑点,则它们不通过边缘连接。它们在相同位置的点具有不同的颜色,但不满足颜色配对的要求。如果一个立方体有红色和黑色的点,而另一个立方体有两个绿色的点,则它们通过一条边连接,因为在一个位置上它们具有成对的颜色(红色和绿色),而在另一个位置上它们只是不同的(黑色和绿色)。
有16种方法可以用两种颜色为两个点着色(因此,我们有16个立方体)。在您面前布置所有这16种可能性。连接所有满足要求的多维数据集。您的方案中是否有四个多维数据集,每个多维数据集都与其他三个多维数据集结合在一起?
这种完全连接的多维数据集子集称为集团。如果找到一个,您将在两个维度上反驳凯勒假说。但是,您不能-它根本不存在。缺少四个立方体这样的集团意味着凯勒的假设在两个维度上都是正确的。
这些多维数据集与Keller的假设在字面上并不完全相同,但是,您可以假设每个多维数据集代表一个图块。将分配给这些点的颜色视为将立方体放置在空间中的坐标。边缘的存在描述了两个立方体如何相对放置。
如果立方体的颜色相同,则它们表示在空间上等距分布的图块。如果它们没有共同的颜色和颜色对(一个具有黑色和白色,另一个具有绿色和红色),则它们表示部分重叠的图块-不允许填充空间。如果两个立方体具有一组匹配的颜色,而一组具有相同的颜色(一个红黑色,另一个绿黑色),则它们表示具有相同边的图块。
最后,最重要的是,如果它们具有一组成对的颜色和另一组不同的颜色(即,如果它们通过一条边连接),则这些立方体表示彼此接触但略有偏移的图块,因为它们的边缘不完全重合... 这是我们需要研究的条件。通过边缘连接的立方体表示不具有公共边的相邻瓦片-这是驳斥Keller假设所需的布置。
Khiyul说:“他们应该接触,但不能完全接触。”

相同的颜色-相同的布置。
颜色不同,不成对-重叠。
两种成对的颜色和一对相同的颜色是共同的一面。
两种成对的颜色和两种不同的颜色-侧面部分接触。
缩放比例
30年前,Corradi和Shabo证明了数学家可以使用类似的程序来处理Keller假设的任何维度,从而调整实验参数。为了在三个维度上证明凯勒假说,您可以使用216个立方体,其中三个点在边缘,并且可能有三对颜色(但是这里有一定的灵活性)。然后,您需要根据我们上面给出的相同条件,寻找八个彼此完全连接的多维数据集(2 3)。
通常,要证明n个维度上的凯勒猜想,您需要使用具有n个点的多维数据集,并尝试在其中找到大小为2 n的集团。可以假设它代表一种超瓦片(由2 n较小的图块),能够覆盖整个n维空间。
如果您可以找到此超级平铺(没有平铺边的瓷砖),则可以使用其副本覆盖没有平铺边的瓷砖来覆盖整个空间,这将证明Keller的假设不成立。
“如果成功,您可以通过转移覆盖整个空间。密歇根大学的拉加里亚斯说:“没有普通瓷砖侧面的砖块将延伸到整个地板。”
Mackey在第8维上反驳了Keller的假设,找到了256个多维数据集(2 8),因此在第7维上仍要处理该假设,找到了128个多维数据集(2 7)。)。找到这个集团将在第七维上反驳凯勒假说。证明它不存在,您将证明该假设是正确的。
不幸的是,要找到一个包含128个立方体的小集团是一项特别困难的任务。在以前的工作中,研究人员利用了这样一个事实,即从某种意义上说,尺寸8和10可以“分解”为较小尺寸的空间,这些空间更易于使用。在这里这没有用。
Lagarias说:“第七维很不方便,因为7是质数,您不能将其分解为较小阶数的维。” “因此,除了处理这些图形的完整组合之外,别无选择。”
对于一个无助的大脑来说,找到一个128多维数据集可能是一个挑战-但这些都是计算机擅长回答的问题,尤其是在没有帮助的情况下。
逻辑语言
要将搜索点击变成计算机可以处理的任务,您需要根据命题逻辑来表述它。这是一种逻辑推理,其中包括一组限制。
假设您三个正在计划与朋友聚会。您正在尝试创建一个来宾列表,但是存在利益冲突。假设您想邀请Alexei或排除Kolya。您的一个朋友想邀请Kolya或Vlad,或同时邀请这两者。另一个朋友不想呼叫Alexei或Vlad。有了这样的限制,是否有可能创建一个满足这三个条件的来宾列表?
用计算机科学的术语来说,这个问题称为可接受性问题。可以通过在命题公式中描述条件来解决。在这种情况下,它看起来如下,并且A,K和B表示潜在的客人:(A或不是K)和(K或B)和(不是A或不是B)。
计算机通过在每个变量中替换0或1来进行计算,0是变量“ false”或off的值,而1是“ true”或on的值。代替0代替A,我们说没有邀请Alexei,邀请了1。在这个简单的公式中,可以通过多种方式(通过创建来宾列表)替换0和1,并且可能所有的计算机在经过它们后都会得出结论,即不可能满足所有兴趣。但是,在这种情况下,可以用两种方法替换1和0以取悦所有人:A = 1,K = 1,B = 0(邀请Alexey和Kolya)和A = 0,K = 0,B = 1(邀请一个Vlad) )。
求解此类语句的计算机程序称为SAT求解器,其中SAT是可满足性的简称。它检查变量的所有组合,并给出一个单音节的答案-是(是),有一种方法可以满足公式的要求,否(否),不是。

卡内基-梅隆大学的约翰·麦基
“你只是想看看你是否能分配真假值的所有变量,使整个公式为真,如果是的话,就满足了,如果没有,那么没有,说:”托马斯·黑尔斯的匹兹堡大学。
寻找128个立方体的集团的问题是一个类似的问题。也可以将其重写为命题公式,并提供给SAT解算器。从大量的骰子开始,每个骰子有7个点和6种可能的颜色。是否可以对点进行着色,以便根据某些规则将128个多维数据集彼此连接?换句话说,是否可以分配颜色以使单击出现?
单击的问题的命题公式很长,包含39,000个变量。每个值都可以分配两个值之一,即0或1。因此,用于排列值或分配颜色的方法的可能选项数量为2,39,000,这非常非常多。
为了在七个维度上找到有关凯勒假设的问题的答案,计算机将必须检查所有这些组合-并排除所有组合(这意味着不存在大小为128的集团,并且在第七维度上的凯勒假设是正确的),或者至少找到将是一个可行的选择(证明凯勒的假设)。
“如果对所有可能性进行简单的迭代,就会遇到324位数字,” Mackey说。世界上最快的计算机将一直工作到所有时间。
但是,这项新工作的作者发现了计算机如何在不检查所有可能性的情况下给出确定的答案。关键是效率。
隐藏的效率
Mackey回忆起从他的角度来看该项目实际上开始工作的那一天。他站在卡内基梅隆大学办公室的黑板前,与Hijul和Breikensik的两位合著者讨论了一个问题,当时Hijul提出了一种结构化搜索的方法,以便在合理的时间内完成搜索。
麦基说:“那天我的办公室里有个真正的天才。” -我就像在NBA总决赛看韦恩·格雷茨基或勒布朗·詹姆斯。我只是出于记忆而感到鸡皮ump。”
您可以通过不同的方式定制搜索特定的Keller图。假设您桌上有很多多维数据集,并且您要按照凯勒伯爵的规则尝试解决其中的128个问题。假设您正确选择了12个,但是您不知道如何添加下一个。此时,您可以丢弃任何包含128个骰子的配置,其中包括此无效配置12。
麻省理工学院的肖尔说:“如果知道前五个作业不匹配,就不需要寻找其他变量,这通常会大大减少搜索范围。”
效率的另一种类型与对称性相关。对称对象有些相同。身份使我们能够了解整个对象,只研究其中的一部分-看着一个人的一半脸,您就可以完全恢复它。
同样,对于凯勒图,您可以偷工减料。再次想象一下,您正在尝试将桌子上的多维数据集对齐。假设您从桌子的中央开始,然后将手放在左侧。您布置了四个骰子,结果一败涂地。现在,您已经消除了一个初始组合以及所有基于该组合的组合。但是,您可以排除此初始组合的镜像-如果将多维数据集以相同的方式放置在右侧,则可以得到多维数据集的配置。
Hales说:“如果您想出一种解决问题的方法,并且巧妙地考虑了对称性,那么您将大大简化任务。”
四位同事以新的方式利用了这种搜索的效率-特别是他们使对称情况的考虑自动化,而数学家以前几乎是手工处理它们。
结果,他们改进了对大小为128的团体的搜索,以至于他们的程序只检查了大约10亿(2,30),而不是检查2,39,000个配置。这样一来,搜索可能会永远持续一个早晨。最终,仅经过半个小时的计算,他们就收到了答案。
“计算机说不,所以我们知道假说是可行的,”希尤尔说。不可能对128个立方体进行着色以使它们彼此融合,因此可以确定Keller关于第七维的假设。对于覆盖空间的任何瓷砖放置,不可避免地会有至少一对完全接触的边缘。
计算机不仅给出了单音节的答案。他附加了200 GB的长证明以支持该结论。
证明不仅是计算机已验证的所有变量集的计算。这是合乎逻辑的论据,证明不可能存在必要的集团。研究人员将证据输入程序中,该程序通过追踪论证的逻辑来测试形式证据并对其进行验证。
“我们不仅经历了所有选择,而且一无所获。Mackey说,我们经历了所有的选择,并且能够写下不存在这种东西的证据。“我们能够写下不满意的证据。”