Clever Geek Handbook

通过动态JVM字节码生成优化计算的经验

在我的模拟随机变量的小型项目中，我遇到了计算用户输入的数学表达式时性能低下的问题，并且很长一段时间以来，我一直在寻找不同的方法来解决它：我试图用C ++编写解释器，希望这样可以更快，我编写了自己的字节码。事实证明，最成功的想法是生成JVM类并在运行时加载它们。



在学习了KMath之后，我决定将这种优化推广到各种数学结构和在其上定义的运算符。



KMath是一个用于数学和计算机代数的库，在Kotlin中大量使用了面向上下文的编程。KMath分离数学实体（数字，向量，矩阵）和对其的运算-它们作为单独的对象提供，与操作数类型Algebra <T>相对应的代数。 



import scientifik.kmath.operations.*

ComplexField {
   (i pow 2) + Complex(1.0, 3.0)
}


因此，在编写字节码生成器之后，考虑到JVM优化，您可以对任何数学对象进行快速计算-足以在Kotlin中对其进行定义操作。



API



首先，有必要开发一个表达式的API，然后才能进行语言和语法树的语法。它还提出了一个聪明的想法，即在表达式本身上定义代数，以提供一个更直观的界面。



整个表达式API的基础是Expression <T>接口，实现它的最简单方法是直接从给定参数或嵌套表达式中定义invoke方法。尽管最慢，但将类似的实现方式集成到根模块中作为参考。 



interface Expression<T> {
   operator fun invoke(arguments: Map<String, T>): T
}


更高级的实现已经基于MST。这些包括：



  • MST口译员，
  • MST类生成器。


KMath dev分支已经有一个用于将表达式从字符串解析为MST的API，或多或少的最终JVM代码生成器。



让我们继续前进到MST。MST当前有四种节点：



  • 终奌站：

    • 符号（即变量）
    • 数字;
  • 一元运算；
  • 二进制运算。






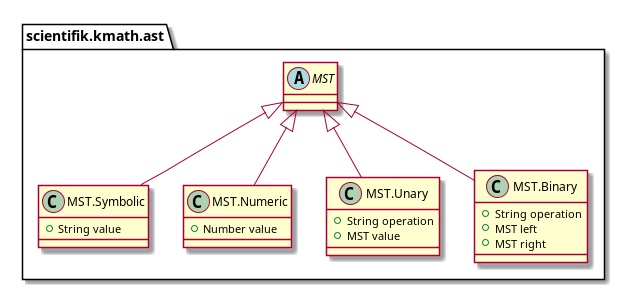
您可以使用它做的第一件事是绕过并根据可用数据计算结果。通过传入目标代数的操作ID（例如“ +”）和参数（例如1.0和1.0），如果定义了此操作，我们可以期望得到结果。否则，在计算时，该表达式将带有异常。







要使用MST，除了表达语言外，还存在代数-例如，MstField： 



import scientifik.kmath.ast.*
import scientifik.kmath.operations.*
import scientifik.kmath.expressions.*

RealField.mstInField { number(1.0) + number(1.0) }() // 2.0


以上方法的结果是Expression <T>的实现，该表达式被调用时会导致遍历通过评估传递给mstInField的函数获得的树。



产生程式码



但这还不是全部：遍历时，我们可以根据需要使用树形参数，而不必担心操作的顺序和操作的繁琐性。这就是用于生成字节码的内容。



kmath-ast中的代码生成是JVM类的参数化程序集。输入是MST和目标代数，输出是Expression <T>实例。



相应的类AsmBuilder和其他一些扩展提供了用于在ObjectWeb ASM之上强制性地构建字节码的方法。它们使MST遍历和类组装看起来整洁，并占用不到40行代码。



考虑为表达式“ 2 * x”生成的类，显示了从字节码反编译的Java源代码： 



package scientifik.kmath.asm.generated;

import java.util.Map;
import scientifik.kmath.asm.internal.MapIntrinsics;
import scientifik.kmath.expressions.Expression;
import scientifik.kmath.operations.RealField;

public final class AsmCompiledExpression_1073786867_0 implements Expression<Double> {
   private final RealField algebra;

   public final Double invoke(Map<String, ? extends Double> arguments) {
       return (Double)this.algebra.add(((Double)MapIntrinsics.getOrFail(arguments, "x")).doubleValue(), 2.0D);
   }

   public AsmCompiledExpression_1073786867_0(RealField algebra) {
       this.algebra = algebra;
   }
}


首先，在这里生成了invoke方法，其中操作数被顺序排列（因为它们在树中更深），然后是add调用。调用之后，将记录相应的桥接方法。接下来，编写代数字段和构造函数。在某些情况下，当不能简单地将常量放入类常量池中时，还会编写常量字段java.lang.Object数组。



但是，由于许多极端情况和优化，生成器的实现相当复杂。



优化对代数的调用



要从代数调用操作，您需要传递其ID和参数： 



RealField { binaryOperation("+", 1.0, 1.0) } // 2.0


但是，这样的调用在性能上是昂贵的：为了选择要调用的方法，RealField将执行相对昂贵的tableswitch语句，并且您还需要记住装箱。因此，尽管所有MST操作都可以用这种形式表示，但是最好直接调用： 



RealField { add(1.0, 1.0) } // 2.0


在Algebra <T>实现中，没有将操作ID映射到方法的特殊约定，因此我不得不插入一个拐杖，其中手动编写了“ +”对应于add方法的拐杖。当您可以找到具有相同名称，所需数量的参数及其类型的操作ID的方法时，也支持某些特殊情况。 



private val methodNameAdapters: Map<Pair<String, Int>, String> by lazy {
    hashMapOf(
        "+" to 2 to "add",
        "*" to 2 to "multiply",
        "/" to 2 to "divide",
...


private fun <T> AsmBuilder<T>.findSpecific(context: Algebra<T>, name: String, parameterTypes: Array<MstType>): Method? =
    context.javaClass.methods.find { method ->
...
        nameValid && arityValid && notBridgeInPrimitive && paramsValid
    }


另一个主要问题是拳击。如果我们查看在编译相同的RealField之后获得的Java方法签名，我们将看到两个方法： 



public Double add(double a, double b)

// $FF: synthetic method
// $FF: bridge method
public Object add(Object var1, Object var2)


当然，不麻烦装箱和拆箱并调用bridge方法会更容易：它出现在这里是因为类型擦除，以便正确实现add（T，T）：T方法，其描述符中的类型T实际上在java.lang之前被擦除了.Object。



直接从两个双打调用add也不理想，因为返回值是铝土矿（在YouTrack Kotlin（KT-29460）中对此进行了讨论，但最好将其调用以将输入对象的两个强制转换最多保存到java.lang中。.Number及其拆箱为double。



解决这个问题花费了最长的时间。这里的困难不在于创建对原始方法的调用，而在于您需要在堆栈上组合原始类型（例如double）和它们的包装器（例如java.lang.Double），并在正确的位置插入boxing（例如，java.lang.Double.valueOf）和拆箱（doubleValue）-绝对不需要使用字节码中的指令类型。



我有想法将键入的抽象悬挂在字节码之上。为此，我不得不更深入地研究ObjectWeb ASM API。我最终转向Kotlin / JVM后端，详细检查了StackValue类（类型化的字节码片段，最终导致在操作数堆栈上接收到一些值），弄清楚了Type实用程序，它使您可以方便地使用字节码中可用的类型（基元，对象，数组）进行操作，并重写生成器使用。通过添加存储下一次调用所需类型的ArrayDeque本身解决了是否对堆栈上的值进行装箱或拆箱的问题。 



  internal fun loadNumeric(value: Number) {
        if (expectationStack.peek() == NUMBER_TYPE) {
            loadNumberConstant(value, true)
            expectationStack.pop()
            typeStack.push(NUMBER_TYPE)
        } else ...?.number(value)?.let { loadTConstant(it) }
            ?: error(...)
    }


结论



最后，我能够使用ObjectWeb ASM编写代码生成器来评估KMath中的MST表达式。通过简单的MST遍历，性能提高取决于节点数，因为字节码是线性的，并且不会在节点选择和递归上浪费时间。例如，对于具有10个节点的表达式，使用生成的类进行的求值与解释器之间的时间差为19％至30％。



在检查了我遇到的问题之后，我得出以下结论：





谢谢阅读。



本文的作者：



雅罗斯拉夫·谢尔盖维奇·波托瓦洛夫（Yaroslav Sergeevich Postovalov）Lavrentyev院士，是在JetBrains Research核物理实验方法实验室的研究员Voytishek Anton Vatslavovich



Tatyana Abramova的带领下建立的数学模型实验室的成员。


More articles:


All Articles