辛几何是一个相对较新的研究领域,影响了许多现代数学。这就是它。

在19世纪初期,威廉·罗恩·汉密尔顿(William Rowan Hamilton)发现了一种几乎具有魔术性质的新几何空间。它将运动和数学编码为一个美丽的几何对象。
从这种现象开始,一个称为辛几何的知识领域得到了发展。在过去的几十年中,它已经从少量的想法发展成为一个充满活力的研究领域,与汉密尔顿几乎无法想象的数学和物理学的更多主题有着密切的联系。
辛几何,实际上是对辛结构的几何空间的研究。但是,需要弄清楚空间具有某种结构的含义-更不用说任何特定的结构了。
几何空间可以像篷布一样灵活,也可以像帐篷一样刚性。西北大学的艾米·墨菲(Amy Murphy)说:“篷布具有延展性,但是如果您扎一堆木棍并为其布置一个框架,则会得到更稳定的结构。”
结构较少的空间只是一堆相互连接的点(例如篷布)。直线是这种一维空间的一个例子。球的表面是二维示例。由于这些空间中没有结构,因此很容易使它们变形,而不会在根本上发生变化。弯曲一条直线;膨胀,弄皱,扭曲球-从拓扑结构的角度来看,研究非结构化空间,它们不会改变。
“从拓扑学家的角度来看,从球的表面开始,您可以随意拉伸它,直到破裂为止,空间对于他们来说并不会改变,”剑桥大学的Isa Keating说。 “他们对图形的一般特征感兴趣。”
自然,当数学家谈论空间变形时,他们并不意味着手动更改空间。它们使用函数来改变空间:该函数包括一个点的坐标,然后一个新点的坐标出现。这种转换将空间中的任何点转换为新的点。这在数学上等同于晃动防水布。
您可以在空间中添加结构。这种结构增强了空间中包含的信息,同时限制了其变形的可能性。

非结构化空间:球的表面是二维空间。没有结构会为其变形提供足够的机会,而不会改变其拓扑特性。

添加结构:通过向空间添加度量结构-就像地球上的经纬线一样,我们可以测量点之间的距离。但是,只有少量的对象变形选项不会违反这些距离。
例如,您可以向球体表面添加度量结构,例如地球上的经度和纬度线。这种结构将使我们能够测量点之间的距离。但是在应用之后,将不再可能在不破坏原始结构的情况下对球进行充气或弄皱-毕竟,我们将更改这些点之间的距离。如果我们给气球充气,例如,纽约和伦敦之间的距离将会增加。
我们可以添加另一种结构-辛。它使我们能够测量空间区域,并允许我们更改空间的形状,以使这些区域不会改变。
汉密尔顿在研究物理系统时发现了这样一个空间的第一个例子-例如行星运动。当行星在太空中移动时,其位置由三个坐标确定,这三个坐标确定了其沿x,y和z轴的位置。代表所有可能的行星位置的点形成三维空间。
汉密尔顿发现,在三维空间中的每个点都可以分配三个附加坐标,以表示行星沿三个轴的动量大小。我们称它们为x m,y m和z m。现在,我们有六个坐标:三个用于位置,三个用于动量。这六个坐标定义了新的六维空间中的一个点。

我们有六个坐标:三个用于位置,三个用于动量。这六个坐标定义了新的六维空间中的一个点。
六维空间是具有辛结构的空间的一个示例,因为它具有测量面积的能力。这就是它的工作原理。
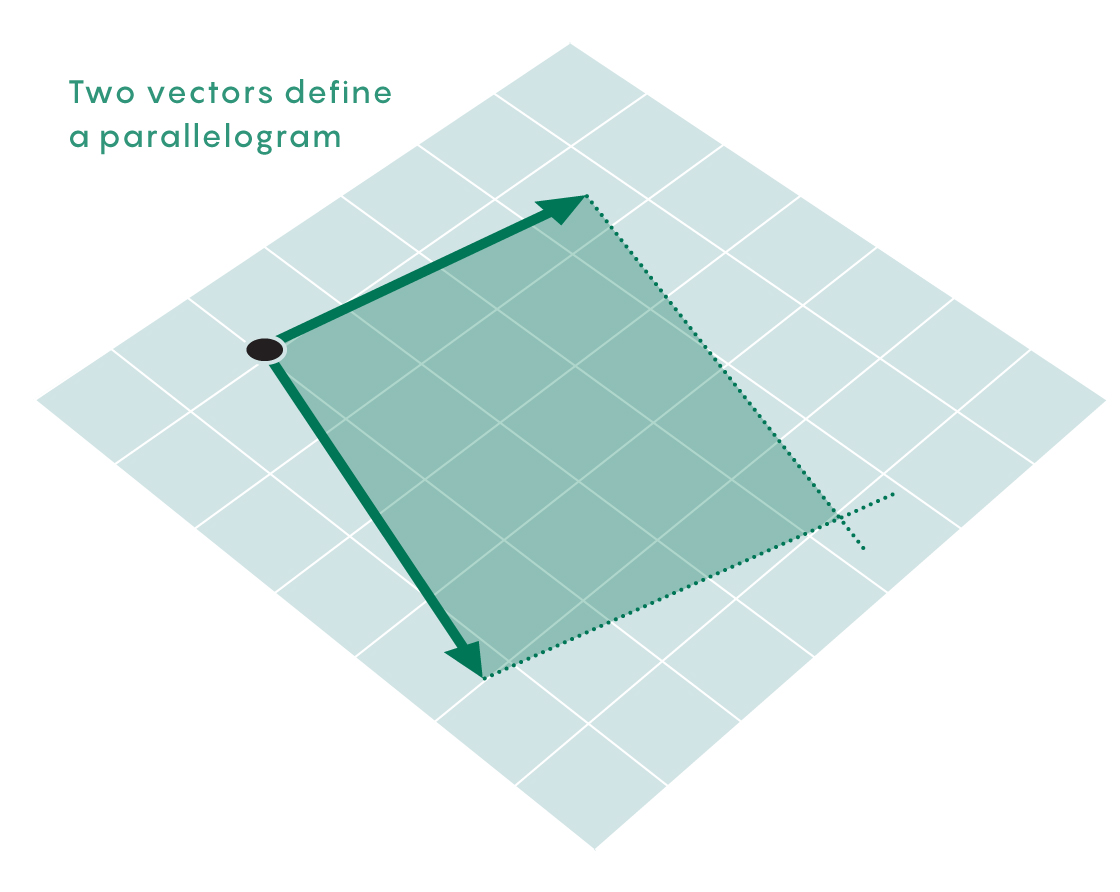
在空间的每个点上,您都可以绘制六个矢量(方向箭头),这些矢量与行星沿着矢量所指向的维度的运动或动量方向相对应。由于两个向量形成一个平行四边形-面积为非零的二维空间-您可以获取两个向量并测量该面积。
为确保该值不为零,您需要采用某些向量对-表示沿同一轴的运动和动量方向。不匹配的向量(例如z轴方向向量和y轴动量向量)会产生面积为零的平行四边形。
这样的向量对还反映了辛空间的另一个重要性质-它们与复数的关系。这些数字的i为-1的平方根,形式为a + bi,其中a为实数,b为虚数。定义六维辛空间的一种方法是定义三个复数,每个复数的两个部分给出一个坐标。这两个部分还对应于我们组合以测量面积的两个向量。
因此,例如,对于每个点,沿x轴绘制的运动方向和动量矢量不仅提供了一种测量面积的方法,而且还组成了定义空间的三个复数之一。这种关系在名称中得到了体现,因为“折衷主义”来自希腊语sumplektikós,与拉丁文的含义相同,即“缠绕在一起”。这个名字反映了辛结构和复数的交织。
这也是辛空间吸引数学家想象力的主要原因之一。墨菲说:“数学家已经对复数和行星运动产生了兴趣。” “因此,如果您向数学家介绍几何的存在,从而说明为什么这两件事是同一基本结构的不同表现形式,那么他肯定会对这个问题感兴趣。”
辛几何学研究保留其辛结构且不改变区域大小的空间变换。此限制不会为允许的转换留出太多余地。结果,辛几何在柔性篷布拓扑和刚性帐篷几何之间占据中间位置。在发现者之后,将保持辛结构的变换称为哈密顿微分形。
但是,汉密尔顿只发现了辛空间的第一个例子,没有理由对此进行详细说明。不久,数学家开始思考在与物理世界无关的几何空间中,辛现象可能是什么样的。
“我们一直想问,数学家们总是在寻求概括性:如果我们不生活在三维空间中,而是生活在三维空间中,那么经典力学将是什么样?”墨菲说。

弗拉基米尔·阿诺德伊戈列维奇提出几个基本假设在辛几何领域
在20世纪60年代,弗拉基米尔·阿诺德伊戈列维奇提出了一些有影响力的假设,描述了辛空间的某些性质,使其比普通拓扑更僵化。其中之一,即关于辛同态的不动点的阿诺德猜想,预言了哈密顿算子具有出乎意料的大量“固定”点,它们在变换过程中不会改变其位置。研究它们,我们可以肯定地说是什么将辛空间与其他类型的几何空间区分开。
在1980年代后期,德国数学家安德烈亚斯·弗洛尔(Andreas Floer)开发了Floer同源性,这是当今数学家用来研究辛现象的强大平台。她使用所谓的。伪全纯曲线,它间接允许数学家计算不动点的数量,确定辛空间应具有的不动点的最小数量。
基廷说:“地板同源性表明,你不能只丢下固定点。” “它使您能够证明这些点必须存在。”
随着辛几何理论的发展,从弦论到低维拓扑以及对令人困惑的数学对偶性(称为镜像对称性)的研究,人们发现了与数学和物理学中越来越多的主题相关的链接。辛几何的应用的一个最新例子是解决方钉的拓扑问题。
但是,对于许多数学家来说,辛几何的吸引力与其与物理学或其他数学领域的交叉点无关。他们认为她的存在是一个奇迹。墨菲说:“我们开始在结构本身中发现美,无论它与其他任何事物有什么联系。”