关系。第一部分

建模的形式理论使用代数关系，包括代数结构模型签名中的代数关系，代数结构描述了真实的物理，技术和信息对象及其运行过程。在后者中，例如，我包括数据库（关系数据库（RDB））。我认为决策领域同样重要，它完全基于关系理论，由两个主要的统计和代数组成。该理论专家的教育水平几乎为零。



打开有关专业化的教科书，您最多只会看到关于等价的内容，作者会以非常特殊的方式对其进行解释。我问一个已经辩护的DTN：您是否通过既不指明关系的承运人又不指明特定的关系来考虑等价关系，在您的记录中它如何看待？答：通常是什么样子。事实证明，他对这一切都有非常模糊的想法。



我发现很难为ReDB的设计命名出版物，但外国文章除外。在90年代，他是一位对手，撰写了一篇论文的评论，该论文考虑了分层，网络和关系数据库。但是，一年零一年半以前，工作需要重新审查，作者只写过关于数据库，关于数据库关系正常化的文章，但并没有表现出理论上的新颖性。许多大学开设的课程都是关于数据库的，而不是关于如何创建数据库，创建DBMS的课程，但通常是关于如何操作现成的（外部）数据库的课程。



版本号工作人员还没有准备好教IT专家创建家用DBMS，OS，编程语言，更不用说LSI，VLSI和定制LSI了。显然，这里的火车已经离开了很长时间。因此，有些面颊虚荣自大（读贪书），这可以从其他人出版物的评论中看出来，向自己表明自己可以，并且不会为自尊而沉迷于别人的无用翻译和重歌-“评级”和“业力”不仅影响缺乏创造力，而且影响简单的教育和养育。



与关系密不可分的第二个领域是决策。我们每个人都在忙于此。没有有意识或无意识的决定，我们就不会举手指。很少有人了解，甚至很少写解决方案。任何决策者（decision-maker）的决策都是基于对替代方案的偏好。偏好模型正是这种类型的关系，称为“偏好关系空间”。但是谁研究他们。当我遇到一个涉及各种类型的关系数量的问题的“专家”时，他不知道答案是“被杀死”，还有一个反问，您为什么需要它？

关系概念

我认为态度一词是每个读者都熟悉的，但是要求定义将使大多数人感到困惑。这件事情是由很多原因导致的。他们最常出现在教师中，如果他们在教学过程中使用关系，就不会专注于这个术语，显然也不会引用令人难忘的例子。



在我的记忆中，有很多令人难忘的例子。关于映射和关系。我将首先讨论映射。有两个油漆桶。一种是白色，另一种是黑色。有一个盒子（很多）。面有压纹数字。您可以用几种方法用两种颜色对立方体的面进行着色？答案是意外的-多达6位二进制数，即2 ⁶=64。让我更详细地解释f：2→6在6中显示2个对象。表的每一行都是fi的离散显示。



让我们构建一个有6列的表格，颜色将与白色-零，黑色-一和立方体的面为列的数字相匹配。我们从所有6个面都是白色的事实开始-这是一个6维零向量。第二行是一个黑色的面，即，最低有效位用1.填充，依此类推，直到用完6位二进制数为止。我们将多维数据集放在一个共同的长行中。它们每个似乎都有一个从0到63的数字。



现在显示反转。一包纸（许多）和6色油漆（毡尖的笔）。

用不同颜色的毡尖笔在纸的两面作标记。需要多少张纸。答案f：6→2或6 ² = 36。这些是任意映射。



让我们继续关系。让我们从一个抽象集开始-关系

A = {a1，a2，a3，...，an}的载体。

你可以在这里阅读。为了更好地理解，我们将集合减少为3个元素，即A = {a1，a2，a3}。现在，我们执行笛卡尔乘法×= ²，

×= {（A1，A1），（A1，A2），（A1，A3），（A2，A1），（A2，A2），（A2，A3 ），（a3，a1），（a3，a2），（a3，a3）}。



我们从A×A得到9个有序元素对，第一个元素来自第一个因子，第二个元素来自第二个因子。现在，让我们尝试从A×笛卡尔正方形中获取所有子集。首先，一个简单的例子。



例子1...给出了由4个元素组成的集合A = {a，b，c，d}。写出其所有子集。 B（A）= {Ø}; {a}; {b}; {c}; {d}; {ab}; {ac}; {ad}; {bc}; {bd}; {cd}; { abc}; {abd}; {acd}; {bcd}; {abcd}; 2 ⁴ = 16个子集。这是集合A的布尔B（A），它包含一个空子集。



子集将从A×A包含不同数量的元素（对）：一个，两个，三个，依此类推，直到所有9对，我们还在此列表中包括空集（Ø）。有多少个子集？很多，即2 ⁹ = 512个元素。



定义。集合的笛卡尔积（我们有一个正方形）的任何子集都称为一个关系。请注意，作品使用相同的集合。如果集合不同，则没有关系，而是对应关系...



如果它是两个因子的笛卡尔积，则该关系为二元关系，如果为3，则为内部关系，如果为4，则为四元关系，而对于n，则为n元。 Arity是关系中的位数。关系被赋予大写字母R，H，P，S的名称。让我们关注二进制关系（BO），因为它们在关系理论中起着非常重要的作用。实际上，其他所有关系都可以简化为二元关系。



关系符号放置在元素R（x，y）的左侧或它们之间x R y处； x，yєA。

定义集合A的所有子集的集合称为布尔值。我们的布尔值包含2 ^{| A×A |}元素，在这里| A×A |是集合的基数。



可以在A = {a1，a2，a3，a4}上以不同的表示形式设置关系：

• 元素枚举；R1 = {（a1，a2），（a1，a3），（a2，a3）（a2，a4）（a3，a2）（a3，a4}
• 二进制n = 16位向量；<0110001101010000>;
• 矩阵;

图1.2。a）二进制关系的4×4矩阵b）矩阵的像元编号



在这里，使用单元号，在图2中用一个单元号填充。1b）

-矢量表示。由元素{0,1}形成代表二进制关系的二进制向量，如下所示：



以向量形式设置关系的经过考虑的示例如下所示：





-图形表示。让我们将集合

A = {x1，x2，z3，...，xn}的元素与平面上的点相关联，即，图的顶点G = [Q，R]。



当且仅当对（xi，xj）єR（对于i = j时，弧（xi，xi）变成顶点（xi）处的环）在图中从（xi）到（xj）画一条弧。 1a）用图表示二进制关系A [4×4]，如图2.2所示。



图2.2。由有向图表示的关系



二元关系目录（n = 3）



在一定距离处可见大。为了体会它们的多样性，我不得不在3个元素的集合上手动创建一个二进制关系目录，其中包括所有（超过500个）关系。在那之后，关系来了又去了。



显然，目录将包括2 ^3×3 = 2 ⁹关系，并且每个关系都将具备一组固有属性。下面（表3）是集合A | | A |中所有512个关系的完整列表。 = 3，共三个元素。还给出了针对载波集的基数（n = 3）的不同子类的各种子类的比率数（表2）的表示结果（表2）。对于每种关系，都指出了其基本属性和所属类型（表3）。表2中列出了该目录中使用的缩写。

表2.不同n的目录的定量特征





使用对二进制关系特别简单和易于理解的示例来解释具有关系的操作的本质及其技术是很方便的。操作可能涉及两个和/或多个关系。对单个关系执行的操作是一元操作。例如，反转（获取逆）关系，进行补码，缩小（限制）关系的操作。一个示例将说明如何使用目录。



例子2。考虑目录表的Npr = 14行。它具有形式



该行的前9个字符（在等号右边）是一个二进制向量，对应于9到2的组合，即第一个单元格的数量（从左到右计数）是二进制关系矩阵的第5个单元格的数量，即 元素a1a1 = a2a2 = 1。在所有关系的列表中，此组合的序列号Ncc = 4，直通号Npr = 14。该行的其余部分包含零或一。零表示缺少对应于零列名称的属性，而零表示在所考虑的关系中此类属性的存在。

关系的性质和定量特征

让我们考虑关系的最重要属性，这将使我们能够在选择和决策理论以及其他应用中进一步强调关系数据库中使用的关系的类型（类）。接下来，我们将用符号[R，Ω]表示关系。R是关系的名称，Ω是关系的载波集。



1.自反性。如果集合中的每个元素与其自身之间的关系为R，则将[R，Ω]关系称为自反（图2.3）。自反BO的图形在所有顶点上都有环（弧），并且关系矩阵包含（E）单位主对角线。





图2.3。反身的态度



2.防反射。如果集合中没有元素与自身相关（图2.4），则[R，Ω]关系称为反身反射。防反射关系称为严格关系。





图2.4。防



反射姿态3.部分反射。

如果集合中的一个或多个元素与其自身不在关系R中，则将关系[R，Ω]称为部分自反（图2.5）。





4.对称。如果关系[R，Ω]与一个有序对（x，y）一起也包含一个有序对（y，x），则称它为对称（图2.6）。





5.反对称。如果对于任何有序对（x，y

）єR，只有在x = y的情况下，有序对（y，x）єR，则关系[R，Ω]被称为反对称。对于这样的比率，R∩R ^- 1⊆E （图2.7）。





6.不对称。如果关系[R，Ω]是抗反射的，则对于关系R∩R ^-1 =Ø的任何有序对（x，y）єR都是有序对（y，x）∉R的关系称为非对称（图2.8）。





7.可传递性。如果对于任何有序对（x，y），（y，z）єR，关系R有一个有序对（x，z）єR或R×R⊆R，则关系[R，Ω]被称为传递。 2.9）。





8.循环性。如果[R，Ω]的元素{x1，x2，z3，...，xn}有一个子集{xi，xi + 1，... xr，...，xj，xi}，则关系[R，Ω]被称为循环为此，可以写出序列xiRxi + 1R ... RxjRxi。这样的序列称为循环或循环（图2.10）。





9.非循环性。没有轮廓的关系称为非循环关系。对于无环的关系，关系R ^ķ ∩R= O满足对任意k> 1（图2.11）。







10.完整性（连接性）。如果对于任何两个元素（y，z）єΩ，其中一个相对于另一个（图2.12），则关系[R，Ω]被称为完全（连接）。线性度。线性关系是最小的完整关系。





图2.12。线性关系



因此，我们已经确定关系作为数学对象具有某些属性，其定义已在前面给出。在下一段中，我们将考虑一些属性的本质和体现：

1. 反射率xєA（xRx）。
2. 抗反射性xєA¬（xRx）。
3. 对称x，yєA（xRy→yRx）。
4. 反对称（xRy＆yRx→x = y）。
5. 传递性；x，y，zєA（xRy＆yRz→xRz）。
6. 循环性 x，yєA; ...
7. 完整性x，y（xRy，yRx）;
8. 连接性（x≠y→xRy，yRx）。
9. 线性度x，yє（xRy，yRx）。

关系空间的分析是该理论的一项复杂任务，应该指出，它还远未完成。主要结果应包括选择关系的子集，这些子集形成具有所有后续后果的完整的关系空间。



这种离散空间的定量关系在

理论和实践上都非常重要。下面考虑与不同类型的关系的性质相关的定量特征的某些方面。

关系运营

像大多数具有关系的数字系统一样，将执行以下操作：

• 一元
• 二进制
• N元。

下表是两个变量x1和x2，mod 2加法和二进制求和的布尔值⊕加法和乘法及表：





上面，引入了二进制关系的概念，作为集合的笛卡尔积的有序对的子集，并且还考虑了关系的性质。此外，还提到了二进制关系和关系的矩阵表示。现在让我们更详细地考虑关系的概念，此外，还要考虑二元关系的基本操作，这是关系中最重要的二元关系。



对于他们，必须满足以下条件：

• 操作中操作数的均值必须匹配；
• 操作的结果必须是相同关系的关系。

对于二进制和n元关系，必须满足以下条件：第一个操作数的到达区域必须与第二个操作数的原始区域匹配。



关系的一元运算关系



倒置。关系R的倒数是比率R ^-1，由条件xR ^-1 y≤yRx定义。更正确地说，由于p·p ^-1 ≠E =Δ ，所以该操作应称为伪反转。



让关系以列出其中包含的有序对的形式编写。如果在每对中交换组件，则新对将形成比率P ^-1，称为P的倒数。



与关系P的逆关系是由（aj ai）єP ^-1的对（ai aj）形成的关系。对于矩阵形式的关系，可通过对矩阵P进行转置来获得逆关系



。9.对关系P的对偶关系（P ^d）是由所有属于普适关系但不属于逆关系的所有对形成的关系（对逆的加法运算）：



P ^d = {（ai aj）| （（AI AJ）★超级×A）（AI AJ）∉ P ^-1）} =（A×A）\ P ^-1。



集合中的对偶和逆关系包含所有对的笛卡尔积A×A，并且不具有公共对，它们像关系P和P一样 形成一个分区A×A





注意，对于任何关系P都不满足P P ＝^d。



缩小（PA1）。关系[R1，A1]被称为关系[R，A]对集合Ω1的限制，如果Ω1⊆Ω并且R1 =R∩Ω1×Ω1。集合A1⊆A上的比率PA1是集合A1上的比率PA1，它由属于关系P的所有对组成，它们同时是笛卡尔积A1×A1的一部分。换句话说，PA1是关系P和A1×A1的交点。令A1 = {a1，a3，a4}，则对于矩阵形式的关系P和Q，缩小关系将具有以下形式：





二进制运算



需要至少两个关系的运算是n元（n元）。只有同一个关系的亲属才能参加这种行动。此类操作的示例：交集，并集，差，关系的对称差等。如果该操作使用两个以上的关系，则对前两个关系依次执行，然后对最终关系和第三个关系依次执行，依此类推。



换句话说，为两个关系定义了这些操作。在关系操作中，假定指定关系的域（操作数和结果）重合，关系的偶数重合，并且操作的结果再次是相同偶数的关系。作为示例，我们将考虑对离散集上定义的二进制关系P和Q进行运算

布尔数组== {a1，a2，a3，a4}（通常，零不适合矩阵）：





1.交点（P∩Q）是由两个关系中包含的所有来自A的所有元素对形成的关系，即 P和Q

共有，P P Q = {（ai aj）| （（（ai aj）єP）＆（（ai aj）єQ）}。



比率矩阵P∩Q是矩阵P和Q的布尔交集：





在没有这样的公共对的情况下，关系的交点被认为是空的，即这是一个空关系。关系R1和R2的交点（R1∩R2）是由A×A的相应子集的交点确定的关系。



2.联盟（PUQ）。关系R1和R2的并集（R1UR2）是由A×A中相应子集的并集定义的关系。由组成比率P或比率Q的所有对形成的比率，即由属于至少一种关系（对联-或并

集）的对PUQ = {（ai aj）| （（ai aj）єP）∨（（ai aj）єQ）}。



如果在集合A×A中不存在不包含在关系PUQ中的其他对，并且它们的交点为零，则将关系P和Q称为合并时的完整关系A×A，并且它们的系统是该完整关系的一个分区。关系矩阵的并集形成为关系矩阵的布尔和：





3.差（P \ Q）是由P中不包含在关系Q中的那些对形成的比率

P \ Q = {（ai aj）| （（（ai aj）єP）＆（（ai aj）∉Q）}。



矩阵表示关系的区别是





4.乘法关系。形成关系的有序对可能包含也可能不包含相同的元素。在组成上具有相同元素的对中，让我们挑出这样的有序对，我们将其称为相邻（邻接）且在第二对中具有第一个元素，而第一对中的第二个元素是相同的。让我们将相邻对的乘积定义为有序对：

（ai ak）∙（ak aj）=>（ai aj）。



在图论方面，这意味着相邻的线对形成从点（ai）到点（aj）的路线，该路线经过点（ak），该点由2个相邻的弧组成。这些弧的乘积是从点（ai）到点（aj）的第三个弧，它绕过中间点（ak）实现了同一方向上的端点之间的过渡。据说弧（ai aj）直接关闭这些点。



5.对称差（P∆Q）是由包含在并集PUQ中但不包含在交点P∩Q中的那些对形成的比率。定义的另一种形式解释了运算的名称：P∆Q由有序对组成，它们是差P \ Q和Q \ P的并集。因此，对称差的表达式可以用两种不同的方式表示：

P∆ Q =（PU Q）\（P∩Q）=（P \ Q）U（Q \ P）。



对称差矩阵为：





从最后的记录可以看出，对称差的运算允许对操作数进行置换，也就是说，它是可交换的。



5.组成或乘积（P∙Q）-由所有对形成的关系，其中：

P∙Q = {（ai aj）|（（ai ak）єP）＆（（ak aj）єQ）}。



换句话说，结果关系中的每个有序对都是相邻对相乘的结果，其中第一对属于第一因子关系，第二对属于第二因子关系。合成操作不是可交换的。



当存在ZєM使得（x，z）єP和（z，y）存在时，集合M上的成分（◦Q）是在包含M（x，y）对的同一集合M上定义的关系R є问



在关系的矩阵表示中，关系的组成矩阵等于原始关系的矩阵的布尔乘积：





关系构成的一种特殊情况是关系的平方。



用归纳法可以证明，关系的第n个级由下式递归定义：P ⁿ = P ^n- 1◦，这意味着在矩阵包含一个链的情况下，对（x，y）єP ⁿ元素：使得（xi，xi + 1）єP，1 <i <n – 1。



合成运算具有关联性（就像矩阵的乘积）。



集合M上的关系的组合是括号的任何排列的关系的成对组合的结果。设置构图结果的区域不变。



由于这些关系矩阵的布尔乘积，形成了布尔关系矩阵的组合。



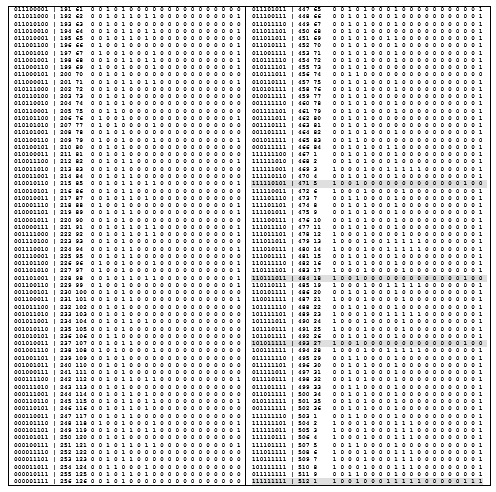
表3.二进制关系的目录（n = 3）可点击