
周期中的其他文章
形式化的形式化理论使用代数关系,包括代数结构模型签名中的代数关系,这些代数关系描述了真实的物理,技术对象及其运行过程。该出版物是前一出版物的续篇,由于需要在此描述许多概念和术语,因此请阅读该出版物。
演示不是以传统的(箭头)样式提供,而是以我本人必须从教科书/手册和杂志文章中代表和掌握整个厨房的方式提供的。我认为我创建的目录特别有用,它允许您选择几乎任何空间并以方便的形式显示其元素:矩阵,图形等。您可以立即查看要处理的内容和属性(它们已经被写出),通常不需要检查。
关系概念
我认为“态度”一词对每个读者都是熟悉的,但是要求定义将使大多数人感到困惑。这件事情是由很多原因导致的。他们最常出现在教师中,如果他们在教学过程中使用关系,则不会专注于这个词,也不会给出令人难忘的例子。文章的一些评论者将评论归因于他们自己的帐户,并增加了缺点。但是您不能将缝制物藏在麻袋中。没有严肃的出版物,也没有。问问自己,您在任何关系空间工作过吗?并诚实地回答自己。关于这个空间,您能告诉世界什么?首先,至少列出其元素并指定属性。您甚至可以通过其创建者的眼光来查看DBMS,但他们也看不到任何东西,或者也看不到任何东西,例如在微电路中。
我在这里重复一遍。应该从抽象集A = {a1,a2,a3,...,an}开始。你可以在这里阅读。为了更好地理解,我们将集合减少为3个元素,即A = {a1,a2,a3}。现在,我们执行所述笛卡尔乘法×= 2和明确地列举笛卡尔平方的所有元素
×= {(A1,A1),(A1,A2),(A1,A3),(A2,A1),(A2,A2 ),(a2,a3),(a3,a1),(a3,a2),(a3,a3)}。
我们从A×A得到9个有序元素对,第一个元素来自第一个因子,第二个元素来自第二个因子。现在,让我们尝试从A×笛卡尔正方形中获取所有子集。子集将包含不同数量的对:一,二,三,依此类推,直到所有9对,我们也将空集合∅包括在此列表中。有多少个子集?很多,即2 9= 512个元素。
定义。笛卡尔方集的子集称为二进制关系。如果有两个因子的笛卡尔平方,则该比率是二元的;如果3的比率是内部的,则4的比率是Fourr,n的比率是n进制。Arity是关系元素中的位数。
定义。集合A的所有子集的集合称为布尔值。布尔值包含2 | A | 元素,在这里| A | 是集合的基数。
关系可以用不同的方式定义:
- 元素枚举;R1 = {(a2,a2),(a2,a3),(a3,a1)}; R2 = {(a3,a3)}
- 二进制向量 <000011100>; <000000001>
- 矩阵;
- 图等方式。
接下来,我们转向关系空间的考虑,假设读者至少在我们在链接中的出版物范围内熟悉关系的概念,关系的性质以及与之的操作。
二元关系空间
让我们初步阐明关系可以是严格的(所有都是抗反射关系)或非严格的(所有其他)。我们将关注冷漠和偏好的关系,后者被分为弱偏好和严格偏好(由于某种原因,不强)。通常,科学中的术语没有顺序,而且很可能不会。例如,在密码术中,在存在密钥的情况下从密码中删除密码就是解密,而在没有密钥的情况下就是解密。似乎解码器解码,但不解码。
具有载波集的二进制关系空间是给定的二进制关系集的任意子集。考虑偏好关系的主要空间(图2.15)。
[R-所有弱偏好关系的空间,满足反射性和完整性的条件。
QT-满足准传递性条件的弱偏好。
QO是线性拟阶的空间,即QT与传递的关系。
TO是所有完美阶的空间,即来自QO的反对称关系。
SP是严格优先考虑的所有关系的空间;它们满足抗反射性和抗对称性的属性。
反渗透-严格的偏序关系,或传递性的严格偏好。由于严格的偏序关系是可传递的,因此自然可以使用它们通过简化的图来表示它们,也就是说,其中省略了传递弧。这样的缩写图称为Hasse图。
QS是准序列的空间,即,严格的偏序,关系I =¬(PUP -1)是等价的。
TSO是严格线性阶数的空间,即满足完整性属性的那些部分阶数。
应该注意的是,总共有n个这样的关系!例如,对于n = 3,完美关系的数目是6,并且它们全部在图1中示出。 2.13。
Ť-所有公差关系(差异)的空间,它们具有对称性和自反性。
TOT是过渡传递容差关系的空间,也就是说,这样的关系使得对I的补码表示为相互逆传递关系的并集,即
¬I=R∩R -1。
我是所有等价关系的空间,即对称,自反和及物关系。
E-等式关系空间,由对角矩阵表示的一种关系组成。在空间R,P和I之间存在一对一的关系,该关系由偏好关系的映射确定。


图2.15二进制关系空间的方案空间
之间的显式连接用于将决策问题(DM)从一个空间转移到另一个空间,可以在其中以更简单的方式解决它们,然后将所得解决方案返回到原始空间,在该空间中制定了DP。
这些关系在图2中以示意图形式显示。2.14。二元关系(关系的类型)的空间如图2所示。2.15。
等价关系
定义。具有自反性,对称性和传递性三个属性的二元关系σA×A被称为二元等效关系(BOE)。表示等价关系σ(x,y),(x,y)∊σ,xσy,x≈y。使用关系的矩阵(表格)表示形式很方便。下面的图2.24只是一个矩阵表示。在这4个元素集的上方,有15个BOE,均已描绘。
等价关系结构的表示和分析(n = 4)
二元关系的等价也许是最常见的BO。没有这种概念的科学管理很少,但是即使用等价性陈述任何问题,也很难理解作者的意思。即使正确定义和枚举了这种二元关系中固有的属性,仍然存在感知上的困难。
让我们从一个等价示例开始,该示例说明了其数量的局限性。
例子1。设三个立方体。让我们列出这些多维数据集所具有的属性,以及这些属性的实际使用(多维数据集的属性)使它们可以互换。让我们为多维数据集分配数字,并在表1中表示其属性。
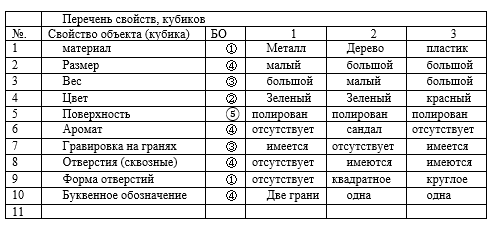
对于每个属性,都会出现BOE和等效类。继续列出属性,我们将不会获得新的等价关系。只会重复已经建造的建筑,但会出现其他迹象。让我们展示BOE和集合之间的联系。
考虑一组三个元素A = {1,2,3},并为其获取所有可能的划分为所有部分的分区。 ①1| 2 | 3; ②12| 3; ③13| 2; ④1 | 23; ⑤123。最后分裂成一个部分。分区编号和BO圈。
定义。集A的一个分区是一个族i,i = 1(1)I,它是的非空成对不相交子集,它们的并集形成整个原始集=Ui,i∩j=∅,∅i≠j。子集i被称为原始集分区的等价类。
这些都是集合的所有分区(5个)。 BO分析表明,也只有5种不同的等价关系。这是巧合吗?我们可以将每个分区与9个单元格(3×3 = 9)的矩阵相关联,每个单元格包含来自集合A的有序元素对,或者如果对应对没有对象,则该单元格保持为空。矩阵的行和列用集合A的元素标记,并且行-列交点对应于有序对(i,j)。它不是适合矩阵单元的一对,而仅仅是一个或零,但是,通常根本不写零。
不,这并非偶然。事实证明,集合的每个分区与BOE一一对应,并且集合的基数可以是| A = n。
就科学循环的使用而言,这种关系也许是最常见的,但是在这方面实现的特性的组合极大地限制了它的流行。
因此,在一组三个元素(总共2 9 = 512个关系)上的所有抽象二进制关系中,只有五个是等价物-所需属性的载体小于百分之一。
对于| A | = 4关系存在2 16= 65536,但只有15个等效项。这是一种非常罕见的关系。另一方面,等价关系在应用问题中很普遍。无论哪里存在并且被认为是非常不同的对象的集合以及这些集合(不是数字)的不同部分的划分,都会出现等价关系。可以将它们称为此类分区的数学(代数)模型,根据各种标准对对象集进行分类。
由一个元素子集A = U {a}组成的集合A的最小分区和由集合{A}本身组成的分区A称为琐碎(不适当)的分区。
格子(4):集合的所有分区= {a1,a2,a3,a4} = {1,2,3,4}

等价关系P15,称为等价或单位关系,对应于最小划分。每个等价类都包含一个元素。对于仅包括集合A本身的集合A的分区,存在一个等效关系,该等效关系包含笛卡尔正方形A×A的所有元素。

与等价关系最接近的类型是公差关系。公差关系集包含所有等效关系。对于载体A,具有三个公差8。它们都具有反射性和对称性。
当传递性满足时,八个容差中的五个会转换为等效值(图2.24和2.25)。
定义。集合A的元素的等价类集合[a]σ被称为集合A的等价集的商集(用A /σ表示)。
定义。自然(规范)映射f:A→A /σ是f(a)= [a]σ的映射f。
公差关系及其分析
这些BO已在前面提到过,但是在这里我们将对其进行更详细的讨论。每个人都知道对象的相似性,相似性,相似性,不可区分性,可互换性的概念。它们的内容似乎相似,但不完全相同。当仅为对象指示相似性时,就不可能将它们分解为清晰的类,以使一个类中的对象相似,并且不同类的对象之间没有相似性。在相似的情况下,出现模糊的情况,没有明确的界限。另一方面,相似对象中微小差异的累积会导致完全不同的对象。
在上一部分中,我们讨论了对象相似性(等效性)关系的有意义的含义。同样重要的是必须建立对象相似性的情况。
让我们研究几何体的形状。如果对象的形状(例如,立方体)的相似性意味着它们在一定的学习情况下具有完全的互换性,则相似性就是部分互换性(当立方体之间存在与它们非常相似的平行六面体),也就是说,与某些立方体具有互换性的可能性(在这种情况下是允许的) )的损失。
相似性的最大衡量标准是不可区分性,而不是乍一看似乎完全相同。身份是质上不同的属性。身份只能被视为不可区分和相似的特例。
关键是不可区分的对象(以及相似的,相似的对象)不能划分为类,因此每个类中的元素都不会不同,并且不同类中的元素显然也不同。
实际上,我们将考虑平面上的点集(x,y)。令值d小于眼睛的可分辨性阈值,即d是这样的距离,在该距离处位于该距离的两个点合并为一个点,即d。视觉上无法区分(在与观察者选定的平面距离处)。现在考虑位于一条直线上的n个点(彼此相邻)的距离为d。每对
相邻的点是无法区分的,但是如果n足够大,则第一个点和最后一个点将彼此相距很远,并且肯定可以区分。
研究相似性或不可区分性的传统方法是首先确定相似性的程度,然后检查相似对象的相对位置。英国数学家Zieman在研究视觉设备的模型时,提出了相似性的公理定义。因此,研究相似性的属性成为可能,而无论在给定情况下如何精确地指定相似性:对象之间的距离,某些特征的重合或观察者的主观意见。
让我们介绍相似性或不可区分性的概念。
定义。集合M上的关系T是自反性和对称性的,称为公差或公差关系。
该定义的正确性从以下事实中就可以看出,即对象与自身之间显然是无法区分的,并且当然看起来像自己(这给关系带来了反射性)。考虑两个对象的顺序不会影响有关它们的相似性或不相似性(对称性)的最终结论。
从平面上的点在视觉上无法区分的示例中,我们看到并非所有对象对都满足公差的传递性。
同样清楚的是,由于相似性是相似性的特例,因此等效性必须是公差的特例。比较等效和容忍的定义,我们相信事实就是如此。哲学上的原则:“特定的事物比一般的事物丰富”已得到明确证实。附加属性-可传递性使某些公差关系等效。两个双胞胎非常相像,他们可以互相参加考试而没有风险。但是,如果只有两个学生是相同的,那么这种技巧虽然可行,但却是有风险的。
集合中的每个元素都包含有关与之相似的元素的某些信息。但是,并非所有信息都一样,就像相同的元素一样。在此,一个元素相对于另一个元素可能包含不同程度的信息。
让我们考虑以不同方式设置公差的示例。
例子2。集合M由四个字母的俄语单词组成-在主格情况下为普通名词。如果这些词相差不超过一个字母,我们将称它们为相似词。准确地说,众所周知的问题“把苍蝇变成大象”的表述如下。找到一个以单词“ fly”开始,以单词“ elephant”结束的单词序列,在给定的定义中,任意两个相邻的单词都相似。解决此问题的方法:
飞-村-土拉-塔拉-卡拉-喀尔-咖啡馆-卡夫尔-穆瑟-小船-钩-鳄鱼-时间-股票-gro吟-大象
例子3...令p为自然数。我们用Sp表示集合M = {1,2,...,p}的所有非空子集的集合。集合Sp上的“具有至少一个公共元素”的关系是公差关系。然后,如果两个这样的子集具有至少一个公共元素,则称为“容忍”。不难看出,关系的反射性和对称性得到了满足。
集合Sp称为(p –1)维单形。该概念将分段,三角形和四面体的概念推广到多维情况。数字1、2、3,...,p被解释为单纯形的顶点。两元素子集-作为边缘,三元素-作为平坦(二维)面,其他k元素子集-作为(k –1)-维面。 Sp的所有元素(子集)的数量等于2 p -1。
子集(面)的容差意味着它们具有共同的顶点。
定义。具有公差关系τ的集合M称为公差空间。因此,公差空间为一对(M,τ)。
例子4。公差Sp的空间可以推广到无限的情况。令H为任意集。如果SH是集合H的所有非空子集的集合,则SH上的公差关系T由条件给出:X X Y如果X∩Y≠∅。这种关系的对称性和自反性是显而易见的。 SH空间标记为<H,T>,并称为公差的“通用”空间。
例子5...令p为自然数。我们用Bp表示p维空间中所有坐标等于0或1的点的集合。Bp中的公差由以下规则指定:x和y包含至少一个重合分量(坐标)时,xτy。 Bp中的元素总数为2 r。对于集合Bp中的每个元素x =(a1,a2,...,ap),只有一个元素y =(1- −a1,1-−a2,...,1-ap)不容忍。
显然,Bp由p维立方体的所有顶点组成。
例子6。考虑公差空间,其组成部分具有任何实际值。
特别是,这是笛卡尔平面中所有点x =(a1,a2)的集合。两点的公差意味着它们至少具有一个坐标。这意味着两个公差点位于同一垂直方向或同一水平线上。
对于p的其他值,该空间可以解释为p维空间中的一组点。特别地,每个元素x都可以看作是在自然数{1、2、3,...}集合上定义的数值函数,该函数将每个自然数i分配为:1≤i≤p实数ai(有限数序列)。然后,两个函数x和y的公差表示它们至少在某一点相等。
偏序关系及其分析
有序集是在其上引入了顺序关系的集。定义。如果一个集合A及其上的二元顺序关系R(≤)被称为部分有序(如BOE),则它满足三个条件(一个条件不同):
- 反射率∀x ∊ A(xRx); (抗反射率∀x ∊ A¬(xRx));
- 反对称∀,y ∊(RyyRx→x = y);
- 传递性∀x,y,z ∊ A(xRy&yRz→xRz)。
以防反射的态度,出现了严格的局部秩序。通过包含元素而排序的集合A的所有子集的集合B(A)是部分排序的集合(PA)。通常将部分排序的集合(B(A),⊆)称为布尔值。
如果x> y且元素x∊A POZA A覆盖元素y∊A,并且没有z∊A使得x> z> y。如果x≥y或x≤y,则将一对元素x,y∊A称为可比较元素。
如果在PLA A中,其每个元素对都是可比较的,则A称为线性有序集或链。
如果某些瘟疫B仅由彼此无法比拟的元素组成,则集合B被称为反链...如果PLAG A中的链不能嵌套在自身以外的任何其他链中,则称为饱和链。
饱和抗链的定义类似。最大链(反链)是包含最大元素数的链(反链)。如果中除m之外没有元素∊并且≤m,则
PLM A的元素m被称为最小。如果除M之外没有元素x“更大”,则鼠疫A的元素M称为最大,且
x≥M。如果∀x∊ A x≤y,则鼠疫A的元素y∊A被称为最大值。元素y∊ A PLAG A被称为最小如果∀x∀Ax≥y。对于最大和最小元素,习惯上分别使用名称1和0。它们被称为通用边界。任何鼠疫A最多具有最小的元素,也最多具有最大的元素。在PLA A中,允许有几个最小元素和几个最大元素
。使用Hasse图方便地描绘最终的PLA A,该图是一个有向图,其顶点分布在该图的各个层上并与A中的元素相对应,并且每个圆弧都向下且在且仅当x∊A覆盖元素y∊A。
不会绘制传递弧。 Hasse图表级别包含相同等级的元素,即通过等长路径(根据弧数)与PCM的最小元素连接。
假设B是PLA A的一个非空子集,那么如果对所有y∊B的x≥y且从所有y B的关系z≥y的事实中得出,元素x∊A称为集合B的确切上限(用sup A B表示), z≥x。如果所有y∊B的x≤y且所有y∊ B的条件z≤y表示z≤x,则集合B
的确切下界(用inf A B表示)是元素x∊A。
例子7。给出了两个有限的数值集
A = {0,1,2,...,21}和B = {6,7,10,11}。
CHUM(A,≤)如图所示。 2.26。的所有上限的集合BΔ称为
集合B的上锥。集合∇B的所有下表面的B称为B的下圆锥。

就继承顺序而言,PLA的任何子集也是PLP。如果集合包含最大和/或最小元素,则它们为最大(分别为最小)。反之则不正确。布尔值具有一个最小(Ø)和一个最大元素。
在给定的集合中,最小元素为零(0),并且与唯一的最小元素一致,并且最大元素不存在。最大元素为{19,20,21}。 B = {6,7,10,11}的确切上限是元素21(这是上圆锥体中的最小元素)。
一般情况。给出一个集合,其基数为*******。在该集合上所有可能的二元关系中,让我们挑出二元偏好关系和相关的严格偏序关系。
偏序与严格偏序的不同之处仅在于它们包含其他元素(在矩阵表示中-对角线元素)(i,ai)= 1,i = 1(1)n,以及这些和其他订单在完整关系集中的数量相同。到现在为止,还没有发现任何依赖关系(公式,算法)可以使任何n的偏序数计算和枚举。
不同的作者已经通过直接计算确定并发布了以下结果(表2.12)。
作者的计算实验使得不仅可以获得数量,而且还可以获得关系乘数-载体的不同幂次的偏序的形式(表示)。印刷商对印刷如此庞大的清单感到cho不休,但不仅美丽需要牺牲,科学也不会拒绝它们。

表2.12显示:n = | A | -集合载波的基数;第二行是集合A上所有二进制关系的数目;进一步
|在(n)中| -非同构关系的类数;
|(n)| -偏序关系的数量;
| Gn(n)| -非同构偏序关系的类数;
| gl(n)| = n! -线性顺序关系的数量。
如您所见,在小n的表中,例如G(n = 4),仅给出219个数据,其值随着n的增加而非常快速地增长,这使使用计算机进行定量(和定性)直接分析变得非常复杂。
下表说明了从每个部分阶与每个线性部分阶的交点生成所有部分阶的Γ(n = 4)的可能性。但是在这种情况下,会出现冗余(重复)的冗余,对于较小的n可以手动将其切断(重新计算)。结果是有300个矩阵,但其中只有219个PL,尚未获得通用公式。在全球范围内,情况相似,尽管我没有看到任何有关西方作者转让PLM的出版物。我们的算法完全是原创和开创性的。
我将给出一个可能的方案来解决枚举偏阶空间元素(n = 4)的问题。

线性顺序(n = 4)的字典顺序中的严格偏序集是由它们的相互交集生成的。


数学上的几个重要定义,用于课本中经常发现的概念。
定义。封闭间隔是一组{x:a≤x≤b}的形式;一个打开间隔不是封闭的,而是一个半打开间隔,即一组{x:a <x≤b}的形式,其中a <b或{x:a≤x <b}的形式既不开放也不封闭。
定义。在通常的实数拓扑中,实线的任意间隔的边界仅由该间隔的两端组成,而不管该间隔是打开,闭合还是半打开。有理数集的边界以及所有无理数集的边界是整个实数集。
定义...每个线性排序集(在其元素最小的任何非空子集中)都称为良好排序。
定义。当且仅当对于元素A和B中的任何一个,A⊂B或B⊂A时,R族称为链(有时是塔,巢)。此条件等同于这样的断言,即R族是通过包含或在公认的术语中线性排列的-家庭R和包含关系是一个链。
P r和n c以及p m a至s和ma n关于s t和H a u s d o r f a。对于集合A的任何族和由族A的元素形成的任何嵌套R,在A中包含R
的最大嵌套M。关于集合及其族的重要定理(J.L. Kelly“一般拓扑”第55页)。
定理。 (a)关于ELEMENT的PRINTSIpMakSIMALN。如果对于A中的每个嵌套,A中有一个包含该嵌套中任意元素的元素,则存在集合的族A中的最大元素。
(b)PRINTSIpMINIMALNO元素。如果对于A中的每个嵌套,此嵌套的每个元素中都包含A中的一个元素,则存在族A中的最小元素。
(c)引种玉和。每个系列的有限字符都有一个最大元素。
(d)LEMMA KURATOVSKOGO。 (部分)有序集中的每个链都包含在某个最大链中。
(e)特森的引理。如果某个部分有序集合的每个链都在上面有界,则该集合具有最大元素。
(f)A至s和o m以及一个选择。令Xα是索引A集合中每个元素a的非空集合。然后在A上存在一个函数c,使得c(a)A A中每个a的Xα。
(g)假定Tserm埃洛。对于任何不相交的非空集的族A,都有一个集C,使得A中每个A的AUC恰好由一个点组成。
(h)PRINTS和P以完整的交付顺序。每套都可以完全订购。