
在进行科学研究和应用研究时,通常会创建模型,其中考虑某些空间的点和/或向量。例如,椭圆曲线密码模型使用仿射和投影空间。当需要加快计算速度时,它们求助于投影,因为在操纵投影空间内得出的椭圆曲线的点的公式中,没有除以坐标的除法运算,在仿射空间的情况下不能绕过该运算。
除法运算只是最“昂贵”的运算之一。事实是,在代数场以及相应的组中,根本没有除法运算,并且出路(当无法不除法时)是除法运算被乘法代替,而不是乘以坐标本身,而是乘以其反数值...因此,我们首先需要涉及扩展的欧几里得算法GCD和其他一些东西。简而言之,并非所有事情都像大多数有关ECC的出版物所描绘的那样简单。几乎所有关于此主题的出版物,不仅是在Internet上,我都熟悉。这些出版物不仅不称职,而且fan亵,这些评论的评价者在评论中加上了作者,也就是说,他们既没有差距也没有明显的错误。关于一篇普通的文章,他们写道它已经是第100500条,并且其影响为零。这就是哈布雷的一切安排,出版物的分析量很大,但内容的质量却不高。这里没有什么可反对的-广告是业务的引擎。
线性向量空间
对周围世界现象的研究和描述必然导致我们引入和使用许多概念,例如点,数字,空间,直线,平面,坐标系,向量,集合等。
让r <3>=三维空间的<r1,r2,r3>向量,指定一个粒子(点)相对于原点的位置。如果考虑N个元素,则其位置描述需要指定3∙N个坐标,可以将其视为3N维空间中某些矢量的坐标。如果我们考虑连续函数及其集合,那么我们来到维数等于无穷大的空间。在实践中,它们通常被限制为仅使用这种具有有限数量维的无限维坐标函数空间的子空间。
例子1。傅里叶级数是使用函数空间的一个示例。考虑傅立叶级数中任意函数的展开
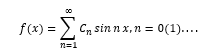
可以将其解释为“向量” f(x)扩展为无限数量的“正交”基向量sinnx,
这是向量概念的抽象和扩展到无数维的示例。确实,对于-π≤x≤π

如果我们从抽象矢量空间的维度(3、3N或无穷大)中进行抽象,那么进一步考虑的本质将不会受到影响,尽管对于实际应用而言,有限维字段和矢量空间更受关注。
如果向量r1,r2,…的集合也属于线性向量空间L,则该向量的任意两个元素之和也位于该集合中,并且将元素与数字C相乘的结果也包括在内。让我们立刻保留一个数字C的值可以从定义明确的数字集F中选择-残数字段以质数p为模,被认为是附加到L的。
示例2。一组由n = 5位二进制数组成的8个向量
如果数字Cє{0,1},则r0 = 00000,r1 = 10101,r2 = 01111,r3 = 11010,r4 = 00101,r5 = 10110,r6 = 01001,r7 = 11100形成矢量空间L。这个小示例使您可以验证其定义中包含的向量空间的属性的体现。
这些向量的求和是按位模2进行的,即不将其传输到最高有效位。请注意,如果所有C都是实数(一般情况下C属于复数字段),则向量空间称为实数。
形式上,向量空间的公理写为:
r1 + r2 = r2 + r1 = r3; r1,r2,r3єL-加交换性和闭合性;
(r1 + r2)+ r3 = r1 +(r2 + r3)= r1 + r2 + r3-加法关联性;
ri + r0 = r0 + ri = ri; ∀i,ri,r0єL-存在中性元素;
ri +(-ri)= r0,对于∀i有一个相反的向量(-ri)єL;
1∙ri = ri∙1 = ri存在一个乘法单位;
α(β∙ri)=(α∙β)∙ri; α,β,1、0是数域F的元素,riєL;标量乘法是关联的;乘法的结果属于L;
(α+β)ri =α∙ri +β∙ri; 对于∀i,ri,L,α,β是标量;
a(ri + rj)= ari + arj对所有a,ri,rjєL;
a∙0 = 0,0∙ri = 0; (-1)∙ri =-ri。
向量空间的维数和基础
在研究向量空间时,有必要澄清诸如构成整个空间的向量数之类的问题。空间的尺寸是多少?向量的最小集合是多少,通过对其求和和乘以一个数字的运算,可以形成空间的所有向量?这些问题是基本问题,不能忽略,因为如果没有答案,就会失去对构成向量空间理论的其他所有事物的理解。
事实证明,空间的尺寸与向量的线性相关性密切相关,并且与可以通过多种方式在研究的空间中选择的线性独立向量的数量密切相关。
向量的线性独立性
如果L的一组向量r1,r2,r3 ...r被称为线性独立的关系

只有在同时平等的条件下才能实现 ...
所有,k = 1(1)p,属于模数为
F = {0,1}的数值余数字段。
如果在某个向量空间L中,可以选择一组p个向量, 只要不是所有 同时,即 原来有可能选择一套,k = 1(1),其中有一个非零的,那么这样的向量 称为线性相关。
例子3。在飞机上的两个向量= <0,1> T和= <1,0> T是线性独立的,因为在关系中(T换位)
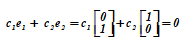
不可能找到任何一对数字 系数同时不等于零,从而满足该比率
三个向量= <0,1> T,= <1,0> T,= <1,1> T形成一个线性相关向量的系统,因为在
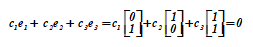
通过选择系数可以确保平等 同时不等于零。而且,向量 是一个功能 和 (它们的总和),表示依赖关系 从 和 ... 一般情况的证明如下。
让至少一个值,例如k = 1(1)p, ,并且关系满足。这意味着向量,k = 1(1),是线性相关的,
让我们明确分离向量r

向量r p被称为向量的线性组合通过剩余向量的r p或r p以线性方式表示,即 r p线性依赖于其他。他是他们的职责。
在二维平面上,任何三个向量都是线性相关的,但是任何两个非共线向量都是独立的。在3D空间中,任何三个非共面向量都是线性独立的,但是任何四个向量始终是线性相关的。
人口的依赖性/独立性{向量通常是通过计算Gram矩阵的行列式确定的(行是我们向量的点积)。如果行列式为零,则向量之间存在相依向量;如果行列式为非零,则矩阵中的向量是独立的。
向量系统的革兰氏行列式(Gramian)
这个系统的Gram矩阵的行列式在欧几里得空间中称为:
哪里 -向量的点积
和 ...
向量空间
的维数和基础空间L的维数s = d(L)被定义为L中形成线性独立集合的向量的最大数目。维度不是L中向量的数目(可以无限),也不是向量分量的数目。
如果
s =∞,则无限维的空间s≠∞的空间称为有限维。
关于确保向量在线性向量空间中生成的向量的最小数量和组成的问题的答案如下。
空间L中线性独立向量的s的任何集合均形成其底和c。这是由于任何向量线性s维向量空间L可以以独特的方式表示为基本向量的线性组合。
我们用符号来固定和表示i = 1(1)s是构成空间L基础的元组之一。
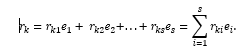
r ki,i = 1(1)s称为向量的坐标 在基础上 ,i = 1(1)s,r ki =(, )。
让我们展示表示法的独特性... 显然,集, 是依赖的,因为 ,i = 1(1)s是一个基础。换句话说,有这样的 不同时等于零 ...
而且,让因为如果 ,然后至少一个 ,它将是非零然后是向量 i = 1(1)s是线性相关的,这是不可能的,因为这是基础。所以,
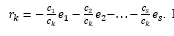
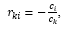

使用“通过矛盾”证明的方法,我们假设书面陈述不仅是这个基础上唯一的一个,还有其他的东西。
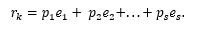
然后我们记下表示的差异,自然地,它表示为:
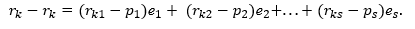
显然,左右两侧相等,但是左侧是向量与自身的差异,即等于零。因此,右侧也为零。向量,i = 1(1)s是线性独立的,因此它们的所有系数只能为零。从中我们得到了
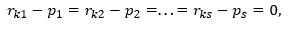
,这仅对于
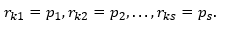
选择的依据。正交性
如果向量的长度等于1,则称为向量。这可以通过将规范化过程应用于任意向量来实现。
如果向量彼此垂直,则称它们为正交。可以通过对每个向量应用正交化程序来获得这些向量。如果一组向量都满足这两个属性,则将这些向量称为正交向量。
需要考虑正交基是由于需要使用一维和多维函数的快速变换。这种处理的任务出现在研究各种目的的通信网络中编码信息消息的代码,研究获得的图像中
通过自动和自动化设备,在许多其他领域使用信息的数字表示形式。
定义。 n维向量
空间V的n个线性独立向量的集合称为其基础。
定理。此外,线性n维矢量空间V的每个矢量x可以以基本矢量的线性组合的形式唯一地表示。字段F上的向量空间V具有以下属性:
0 x = 0(等式左侧的0是字段F的加法组的中性元素;等式右侧的0是空间V的元素,这是加法组V的中性单位元素,称为零矢量);
(-1)·x = –x; –1є F; xєV; –XєV;
如果αx =0єV,则对于x≠0总是α=0。
令Vn(F)为长度为n的所有序列(x1,x2,...,xn)的集合,其中包含字段F,即, Vn(F)= {x,使得x =(x1,x2,...,xn),xiєF;
i = 1(1)n}。
标量的加法和乘法定义如下:
x + y =(x1 + y1,x2 + y2,…,xn + yn);
αx =(αx1,αx2,...,αxn),其中y =(y1,y2,...,yn),
则Vn(F)是字段F上的向量空间。
示例4。在向量空间r2 = {0,1}上的向量空间r?= 00000,r1 = 10101,r2 = 11010,r3 = 10101中,确定其维数和基数。
决定让我们形成一个线性向量空间的向量相加表
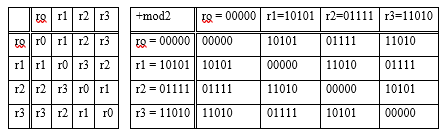
在这个向量空间V = {ro,r1,r2,r3}中,每个向量都有自己的对立面。除r之外的任何两个向量都是线性独立的,因此很容易验证
c1·r1 + c2·r2 = 0; c1 r1 + c3 r3 = 0; c2 r2 + c3 r3 = 0;
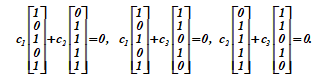
这三个关系中的每一个仅对系数ci,cjє{0,1}对的同时零值有效。
当同时考虑三个非零向量时,它们之一总是其他两个向量的总和或等于自身,并且r1 + r2 + r3 =r®。
因此,尽管每个向量具有五个分量,但是考虑的线性向量空间的维数等于两个s = 2,d(L)= s = 2。空间的基础是集合(r1,r2)。您可以使用对(r1,r3)作为基础。
从理论上和实践上,描述向量空间的问题都很重要。事实证明,任何基向量集都可以看作是矩阵G的行,称为向量空间的生成矩阵。该空间的任何矢量都可以表示为矩阵G的行的线性组合(例如,在这里)。
如果向量空间的维数为k且等于矩阵G的行数,矩阵G的秩,则显然存在k个系数,它们具有q个不同的值,用于生成矩阵的行的所有可能的线性组合。此外,向量空间L包含q k个向量。
来自ℤpn的所有向量的集合加上向量的乘积和来自ℤp的标量的向量相乘的运算是线性向量空间。
定义。向量空间V的子集W满足以下条件:
如果w1,w2єW,则w1 + w2єW,
对于任何αєF和wєW,元素αwєW
本身就是字段F上的向量空间,被称为向量空间V的子空间。
令V为字段F和集合W⊆V上的向量空间。如果W相对于V中定义的线性运算为线性向量空间,则集合W为V的子空间。
表。向量空间的特征
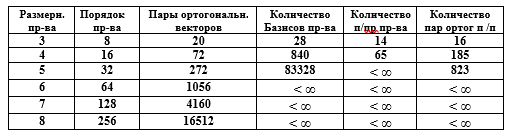
向量空间的矩阵表示的紧凑性是显而易见的。例如,指定50位二进制数的L个向量(其中30个向量构成向量空间的基础)需要形成矩阵G [30,50],并且描述的向量数超过10 9,这在元素方式上似乎是不合理的。
任何空间L的所有基数都被det G> 0的非退化矩阵的子集P划分为两类。其中一个(任意)称为具有正向基数(右基数)的类,另一类包含左基数。
在这种情况下,他们说方向是在空间中给出的。之后,任何基础都是向量的有序集合。
如果两个向量的编号在正确的基础上更改,则基础将变为左侧。这是由于在矩阵G中交换了两行,因此行列式detG将改变符号。
向量的范数和点积
在解决了关于找到线性向量空间的基础,关于该空间的所有元素的生成以及关于任何元素的表示以及通过基本向量的向量空间本身的问题之后,我们可以提出在该空间中测量元素之间的距离,向量之间的角度,向量分量的值的问题,向量本身的长度。
如果实数或复数向量空间L中的每个向量r都可以与实数||关联,则称其为范数向量空间。 r || -矢量模量,范数。单位向量是范数为1的向量。零向量具有零分量。
定义...如果在其中定义了二进制运算,该向量空间将标量分配给来自L的向量的每对ri,rj,则将其称为单一空间。在括号(ri,rj)中,ri(r)的标量或内积被写成(表示),并且为
1。(ri,rj)= ri·rj;
2.(ri,rj)=(ri∙rj)*,其中*表示复共轭或厄米对称。
3.(ri,rj)=(ri∙rj)-关联律;
4.(ri + rj,rk)=(ri∙rk)+(rj∙rk)-分配律;
5.(ri,rk)≥0,从(ri,rj)= 0开始,遵循ri =0 。
定义。平方根的正值
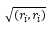 称为向量ri的范数(或长度,模数)。如果
称为向量ri的范数(或长度,模数)。如果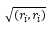 = 1,则将向量ri归一化...如果
= 1,则将向量ri归一化...如果
unit矢量空间L的两个矢量ri,rj的标量积等于零,即它们相互正交,则它们相互正交。 (ri,rj)=0。
对于线性向量空间中的s = 3,选择三个相互垂直的向量作为基础很方便。这种选择大大简化了许多依赖关系和计算。在空间和其他维数s> 3中选择基数时,将使用相同的正交性原理。使用引入的向量的标量积的运算可提供这种选择的可能性。
选择正交归一化向量的向量空间作为基础时,可以获得更大的优势-正交基础... 除非另有说明,否则我们将始终假设以这种方式选择基数ei,i = 1(1)s。
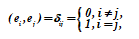
在unit矢量空间中,此选择始终可以实现。让我们展示这种选择的可行性。
定义。令S = {v1,v2,…,vn}是域F上向量空间V的有限子集。
来自S的向量的线性组合是a1∙v1 + a2∙v2 +…+ a∙vn的形式,其中每个ai ∊F。
集S的包络(符号{S})是来自S的向量的所有线性组合的集合。S的包络是V的子空间。
如果U是V中的空间,则如果{S} =,则U被S覆盖(S个合约U)。 。
向量集S与F线性相关,如果在F中存在标量a1,a2,...,a,则不是a1∙v1 + a2∙v2 +…+ a∙vn = 0的所有零。如果没有此类标量,则该集合矢量S线独立地超过F.
如果一个向量空间V由矢量S的线性独立的系统跨越(或系统S合同的空间V),则该系统S要求V.一个基础
将任意基础简化为正交形式
让空间V具有非正交基ē我,I = 1(1)S上。我们用符号表示每个基向量的范数

用于降低的基础上的正交归一形式的程序是基于Gram-Schmidt正交方法,其又通过递推式实现
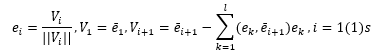
在扩展形式,在此基础正交和归一化算法包括以下条件:
除以E中的矢量1通过它的范数;我们得到的归一化矢量e我= E 1 /(||ē 1 ||);
我们形成V2 = E 2 - (E 1,ē 2)电子1和规范它,我们得到ē 2。显然
(e1,e2)〜(e1,e2)-(e1,e 2)(e1,e1)= 0;
构建V3 = E 3 - (E1,ē 3)E1 - (E2,ē 3)e2和归一化的话,我们得到E3。
对于它,我们立即有(E1,E3)=(E2,E3)= 0。
继续该过程中,我们得到的正交集合E我,I = 1(1)S上。该集合包含线性独立的向量,因为它们都是相互正交的。
让我们确保这一点。让关系
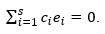
如果集合E我,I = 1(1)s是相关的,则至少有一个CJ系数不等于零CJ≠0
乘以EJ比率的两侧,我们得到
(EJ,C1∙E1)+(EJ,C2∙E2) + ... +(ej,cj∙ej)+…+(ej,cs∙rs)=0
。除(ej,cj∙ej)在正交向量中等于零外,总和中的每个求和等于正交向量的标量。健康)状况。但是,在此项中
(ej,ej)= 1≠0,因此,只有cj可以为零。
因此,假设cj≠0是不正确的,并且集合是线性独立的。
例子5。给出了三维向量空间的基础:
{<-1,2,3,0>,<0,1,2,1>,<2,-1,-1,1>}。
点积由以下关系定义:
(<x1,x2,x3,x4>,<y1,y2,y3,y4>)= x1∙y1 + x2∙y2 + x3∙y3 + x4∙y4。
使用Gram-Schmidt正交化过程,我们得到一个向量系统:
1= <-1,2,3,0>; a2 = <0,1,2,1> -4 <-1,2,3.0> / 7 = <4,-1,2,7> / 7;
a3 = <2,-1,-1,1> +½<-1,2,3,0>-<4,-1,2,7> / 5 = <7,2,1,-4> /十。
(a1,a2)=(1 + 4 + 9 + 0)= 14;
a1 E = a1 /√14;
a2-(a1 E,a2)∙a1 E = a2-(8 /√14)(a1 /√14)= a2-4-∙a1 / 7;
邀请读者独立处理第三个向量。
归一化向量的形式为:
a1 E = a1 /√14;
a2 E = <4,-1,2,7> /√70;
a3 E = < 7,2,1 ,-4>/√70;
在下面的示例6中,给出了详细的详细过程,该过程从简单的基础(随机获取)计算出正交基础的推导。
例子6。将线性向量空间的给定基础简化为正交形式。
给定:基本向量


向量空间的子空间
向量空间结构
多维空间中对象(实体)的表示是一项非常困难的任务。因此,三维立方体具有普通的三维立方体作为其面,并且可以在三维空间中构建三维立方体的展开。在某种程度上,物体或其零件的“图像”和清晰度有助于其更成功的研究。
前面的内容使我们假设向量空间可以某种方式分解,以挑选出其中的部分,称为子空间。显然,对多维空间,尤其是无穷维空间和对象的考虑使我们失去了表示的清晰度,这使得在这种空间中研究对象非常困难
空格。即使看似简单的问题,例如这些空间中多面体元素的数量特征(顶点,边,面等的数量)也无法完全解决。
研究此类对象的一种建设性方法是选择其元素(例如,边缘,面)并在较小尺寸的空间中对其进行描述。因此,一个三维立方体具有普通的三维立方体作为其面,并且可以在三维空间中构建三维立方体的展开。在某种程度上,
物体或其部分的“图像”和清晰度有助于其更成功的研究。
如果L是字段K的扩展,则L可以看作是K上的向量(或线性)空间。字段L的元素(即向量)通过加法形成阿贝尔群。此外,每个“向量” a L可以乘以一个“标量” r k,乘积ra再次属于L(在这里,ra从元素r和该域的a的场L运算的意义上来说只是乘积)。该定律还适用于
r∙(a + b)= r∙a + r∙b,(r + s)∙a = r∙a + r∙s,(r∙s)∙a = r∙(s∙a)和1∙a = a,其中r,sєK,a,bєL。
前面的内容使我们假设向量空间可以通过某种方式分解,以挑选出其中的部分,称为子空间。显然,这种方法的主要结果是减小了所分配子空间的尺寸。令子空间L1和L2在向量线性空间L中被区分。作为L1的基础,选择了比原始L中小的集合ei,i = 1(1)s1,s1 <s。
其余的基础向量生成另一个子空间L2,称为子空间L1的“正交补”。我们将使用符号L = L1 + L2。这并不意味着空间L的所有向量都属于L1或L2,而是来自L的任何向量都可以表示为L1的向量与L2的正交向量之和。
分割的不是向量空间L的向量集,而是维数d(L)和基本向量集。因此,向量空间L的子空间L1是其元素(较低维度)的集合L1,它本身是一个向量空间,对于加法和乘以L中引入的数字而言。
每个线性向量子空间Li-包含零向量,并且与其任何向量一起包含其所有线性组合。任何线性子空间的尺寸都不会超过原始空间本身的尺寸。
范例7。在普通三维空间中,子空间都是通过原点的直线(维数s = 1),平面(维数s = 2)。在次数最多为n的多项式的空间n中,子空间例如是k <n的所有k,因为最多将次数为k的次数多项式相加并相乘,我们将再次获得相同的多项式。
然而,每个空间Pn都作为具有实系数的所有多项式的空间P中的子空间而包含,并且后者是连续函数的空间C的子空间。
实数字段上的相同类型的矩阵也形成线性向量空间,因为它们满足向量空间的所有公理。长度为n的集合的向量空间L2(与长度为n的集合的子空间L1正交)形成一个子空间L2,称为L1的零空间。换句话说,来自L2的每个向量都与来自L1的每个向量正交,反之亦然。
子空间L1和L2都是长度为n的向量空间L的子空间,在编码理论[4]中,每个子空间L1和L2生成线性编码,该线性编码是其他子空间生成的编码的对偶。如果L1是(n,k)码,则L2是(n,n-k)码。如果代码是某个矩阵的行的向量空间,则其对偶代码是该矩阵的零空间,反之亦然。
向量空间Vn研究中的一个重要问题是建立它们的结构(结构)。换句话说,感兴趣的是元素,它们的集合(维度1 <k <n的子空间)以及它们之间的关系(排序,嵌套等)。我们假设在由q =r个元素组成的有限域GF(q)上的给定向量空间Vn,其中是质数,r是整数。
以下结果是已知的。
向量空间的子空间数
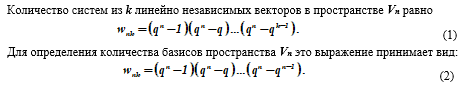
让我们给出以下理由。可以用q n -1种方式选择来自k个线性独立(v1,v2,…,vk)矢量系统的每个矢量v1≠0 。下一个向量v2≠0不能根据v1线性表示,即可以选择q n -q种方式,等等。
最后一个向量vk≠0也不是按照先前选择的向量v1,v2,…,vk线性表示的,因此可以以q n -q k -1的方式进行选择。因此,选择一组向量v1,v2,...,vk的方法总数被定义为单个向量的选择数的乘积,从而得出公式(1)。对于k = n的情况,我们有w= wn,n,并从公式(I)得到公式(2)。

关于子空间维数的重要概括结果。
与长度为n的元组的子空间V1正交的所有长度为n的元组的集合形成长度为n的元组的子空间V2。该子空间V2称为V1的空空间。
如果一个向量与生成子空间V1的每个向量正交,则该向量属于V1的零空间。
(V1)的一个示例是(7,4)Hamming码的生成矩阵的7位向量集,其中7位向量的零子空间(V2)形成该代码的奇偶校验矩阵。
如果长度为n的集合的子空间(V1)的维数等于k,则零子空间(V2)的维数等于n-k。
如果V2是长度为n的元组的子空间,并且V1是V2的零空间,则(V2)是V1的零空间。
令U∩V表示属于U和V的向量的集合,则U∩V是子空间。
令U⊕V表示子空间,该子空间由形式为u u + b v的所有线性组合的集合组成,其中u u U,v u V,ab是数字。
子空间U∩V和U⊕V的总和等于子空间U和V的总和。
令U2为U1的零子空间,V2为V1的零空间。那么U2∩V2是U1⊕V1的零空间。
结论
本文考虑了向量空间的基本概念,向量空间通常用于构建模型以分析加密,编码和隐秘系统以及其中发生的过程。因此,在新的美国加密标准中,使用了仿射空间,并且在椭圆曲线上的数字签名中同时使用了仿射和
投影空间(以加快对曲线点的处理)。
我们不是在谈论工作中的这些空间(您不能将所有内容都集中在一个堆中,而且我也限制了出版量),但是提及这一点并非徒劳。关于保护手段和密码算法的作者天真地相信,他们了解所描述现象的细节,但是对欧几里得空间及其性质的理解却毫无保留地转移到具有不同性质和规律的其他空间。阅读的读者被误导了该材料的简单性和可访问性。
在信息安全和特殊设备(技术和数学)领域中制造了对现实的错误印象。
总的来说,我是主动的,读者有多幸运。
文学
1. Nadobin A.A. Avdoshin S.M.离散数学。模块化代数,密码学,编码。 -M .: DMK出版社,2017.-352羽
2. Akimov O.E.离散数学,逻辑,组,图形-M。:Lab。Base。锌。2001.-352羽
3.安德森(Anderson D.A.)离散数学和组合数学),莫斯科:威廉姆斯,2003年,第960页。
4. Berlekamp E.代数编码理论。 -M .:米尔(Mir),1971.-478羽
5. Vaulin A.E.计算机安全问题中的离散数学。 H 1- SPb。:VKA图片。 A.F.莫扎伊斯基,2015.219羽
6. Vaulin A.E.计算机安全问题中的离散数学。 H 2- SPb。:VKA即时。 A.F.莫扎伊斯基,2017.-151羽
7. Gorenstein D.有限简单组。它们的分类简介。-M。:Mir,1985.- 352 p。
7. Graham R.,Knut D.,Ptashnik O.具体数学。信息学的基础.-M .: Mir,1998.-703 p。
9. Elizarov V.P. -M。:Helios ARV,2006年。 -304羽
伊万诺夫(Ivanov B.N.)离散数学:算法和程序-M。:Lab.Baz。知识,2001.280羽
10. Yerusalimsky Ya.M.离散数学:理论,问题,应用-M.:Vuzovskaya kniga,2000年-280页。
11. Korn G.,Korn T.《科学家和工程师数学手册》。-M。:Nauka,1973年。-832页。
12. Lidl R.,Niederreiter G.有限领域:2卷,第1卷-M .:米尔,1988年。 -430羽
13. Lidl R.,Niederreiter G.有限领域:2卷。第2卷-M .: Mir,1988年。 -392羽
14. Lyapin E.S.,Aizenshtat A.Ya.,Lesokhin M.M.,关于群体理论的练习。-莫斯科:Nauka,1967年-264页。
15.喃喃自语 抗干扰信息传输的基础。-L Energoatomizdat,1990,288羽
16. Nabebin A.A.离散数学.. M .:实验室基础。知识。,2001.280羽
17.诺维科夫 程序员的离散数学。-SPb。:Peter,2000.-304 p。
18. Rosenfeld B.A. 多维空间。-M。:娜卡(Nauka),1966.-648羽。
18. Hall M.群论。-M。:伊兹德。伊利诺伊州,1962.-468羽
19. Shikhanovich Yu.A. 组,环,格子。-SPb。:Kirtsideli,2006年。-368羽
20. Shneperman LB 代数和数论问题与练习的过程:2小时内第2部分。-Mn。:Vysh。shk。,1987.-256羽
21. Shneperman LB 代数和数论中问题的集合-明斯克:Design PRO,2000年-240页。