两位数学家证明了埃尔德最喜欢的关于数字序列模式的猜想的第一阶段

几个数学家已经证明了最著名的关于整数可加性的假设的第一部分。匈牙利数学家帕尔·鄂尔多斯(Pal Erdos)是60多年前提出的。听起来是这样的:在无限个整数列表中的什么时候,可以保证至少三个彼此等距间隔的数字的模式-例如26、29和32。
鄂尔多斯在职业生涯中提出了成千上万个问题,但问题是,哪个数字列表包含彼此等距的数字(数学家称之为算术级数)是他的最爱之一。剑桥大学的蒂莫西·高尔斯(Timothy Gowers)说:“我认为很多人将这视为Erds的主要关切。”高尔,谁收到1998年获得菲尔兹奖,花费了许多时间来解决这个问题。他说:“几乎所有雄心勃勃的加法组合数学家都试图解决这一问题,”他指的是该假设所属的数学领域。
与稀疏数字相比,数字的Denser列表通常更可能包含算术级数。因此,Erds提出了一个简单的检查列表密度的方法:将列表中那些值的反值相加。如果有足够的数字使该和为无穷大,那么根据Erdös的说法,列表应包含无数个任意有限长度的算术级数-三,四等。连续的数字。
在7月7日在线发表的一篇论文中,剑桥大学的Thomas Bloom和Olaf Sisask来自斯德哥尔摩大学的研究证明了在数字三元组等距分布(例如5、7和9)的情况下的这一假设。这对表示,当列表中数字的倒数之和为无限大时,其中的等距数必须是无穷三倍。

剑桥大学的托马斯·布鲁姆(Thomas Bloom)
“这是多年来最出色的成绩,”加州理工学院的Nets Katz说。 “这是一个重大事件。”
一组,即趋于无穷大的倒数之和,是质数-只能被1和它们自己整除的质数。在1930年代,约翰内斯·范德库普使用质数的特殊结构表明,在质数中确实可以找到无数个等距的三元组(例如17、23和29)。
但是,Bloom和Sisask的新发现意味着,无需证明素数的独特结构即可证明其中有无限数量的三元数。仅仅知道有足够的质数就可以使它们的倒数之和成为无穷大-这已经被数学家们认识了很多世纪了。 “托马斯和奥拉夫的研究结果告诉我们,即使它们的结构与实际结构完全不同,仅拥有大量结构就可以保证算术级数无穷大,”汤姆·桑德斯(Tom Sanders)写道。来自牛津大学。
新书长77页,数学家需要花费一些时间进行彻底检查。但是,许多人对此表示乐观。卡茨说:“这看起来确实像是这种说法的证明,”他的早期工作构成了这一基础。
Bloom和Sisask的定理说,如果数字列表足够密集,则应在其中出现某些模式。这项发现与数学的基本座右铭相一致,正如牛津大学的萨拉·皮斯托斯(Sarah Pillus)所称,它是由西奥多·莫兹金(Theodore Motzkin)首次提出的:“没有绝对的混乱”。
伪装密度
如果将稀疏列表创建得足够少,则很容易创建没有算术级数的无限列表。例如,考虑顺序1,10,100,1,000,10,000,... ...倒数加起来为1.111(1)。这些数字之间的距离增长得如此之快,以至于找不到彼此等距的单个数字三元组。
但是,您可能想知道是否有更密集的数字列表,而这些数字仍然没有算术级数。例如,您可以沿着数字线走,留下算术级数中未包括的每个数字。我们得到的序列1、2、4、5、10、11、13、14 ...乍一看看上去很密集。但是,随着时间的流逝,它变得越来越稀疏-例如,当我们获得20位数字时,我们将从数字行中仅提取所有整数的009009%。 1946年,Felix Berend提出了更密集的示例,但它们也变得非常稀疏-Berend集达到20位数字,只包含所有整数的0.001%。
另一方面,如果您的集合几乎包含所有整数,那么它将肯定包含算术序列。但是在这两个极端之间是一个广阔的,几乎没有标记的中间领土。数学家推测,集合的稀疏程度如何,以便在那里仍能保证算术级数?

斯德哥尔摩大学的Olaf Sisask
鄂尔多斯(正如他们所说,可能与匈牙利数学家帕尔图兰一起)给出了一个可能的答案。其求和的条件是掩膜密度。事实证明,这与说直到数字N的列表的密度不小于1除以N中的位数的意思是相同的。换句话说,当您沿数字线移动时,列表可能会越来越稀疏,但前提是它发生的非常缓慢。对于5位数字,列表的密度应至少为1/5; 20位数字-至少为1/20,依此类推。如果满足此条件,那么正如鄂尔多斯所建议的那样,您的列表应包含无限数量的任意长度的算术级数。
1953年,克劳斯·罗斯(Klaus Roth)使数学家走上了证明Erds猜想的道路。在那年为他赢得菲尔兹奖的论文中,他定义了一个密度函数,该函数可以保证等距的三元组数字。密度不像Erds那样低,但是当我们沿着数字线移动时,密度却接近零。罗斯定理意味着在其密度最终低于1%,然后低于0.1%,然后低于0.01%等的数字列表中,如果仅密度下降足够,则必须进行算术级数运算慢。

1991年6月,帕尔·埃德(Pal Erd)在剑桥大学的讲座“数学60年”。
首先,Roth的方法基于这样一个事实,即大多数具有他选择的“希望”密度的列表具有算术级数-它们具有足够多的数字对,因此几乎可以肯定的是,这些对之间的一些中点也会出现在该列表上,会导致出现等间距的三胞胎。诀窍是如何从“几乎所有”数字的列表转到“所有”数字的列表,即使可以对整个结构进行特殊设计以避免算术级数。
收到了这样的清单后,罗斯想出了如何通过使用傅立叶变换标记“频谱”来“提取”其结构的方法...它显示了哪些新兴模式最为明显-相同的数学是X射线晶体学和放射光谱学等技术的基础。
有些频率看起来比其他频率更强,并且这些变化强调了现有的模式-例如,频率可能表明列表包含的奇数比偶数更多。如果是这样,那么您只能专注于奇数,并获得比仅奇数列表更密集的列表。 Roth能够证明,经过几次蒸馏,该列表是如此密集,以至于其中必须存在算术级数。
斯坦福大学的雅各布·福克斯 说,在过去的五十年中,罗斯的方法启发了许多分析数论论文。“他的想法很有影响力。”
游戏,设定,比赛
但是,Roth的方法仅适用于从一开始就已经很密集的那些数字集;否则,不断蒸馏只会简单地蒸发掉所有数字。其他数学家不断发现越来越多地使用此方法的方法,但它们无法接近Erds假设中描述的密度。“这个障碍看起来非常困难,”福克斯说。
然后在2011年,卡兹(Katz)和迈克尔·贝特曼(Michael Bateman)想出了如何以更简单的方式克服这一障碍:在纸牌游戏《赛斯》中,玩家在其中搜索三张标有不同符号的卡组。可以将Set游戏中的三张牌定义为算术级数,就整数列表而言,您可以问一个问题:为了确定至少找到三张牌,您需要在桌子上放多少张牌。
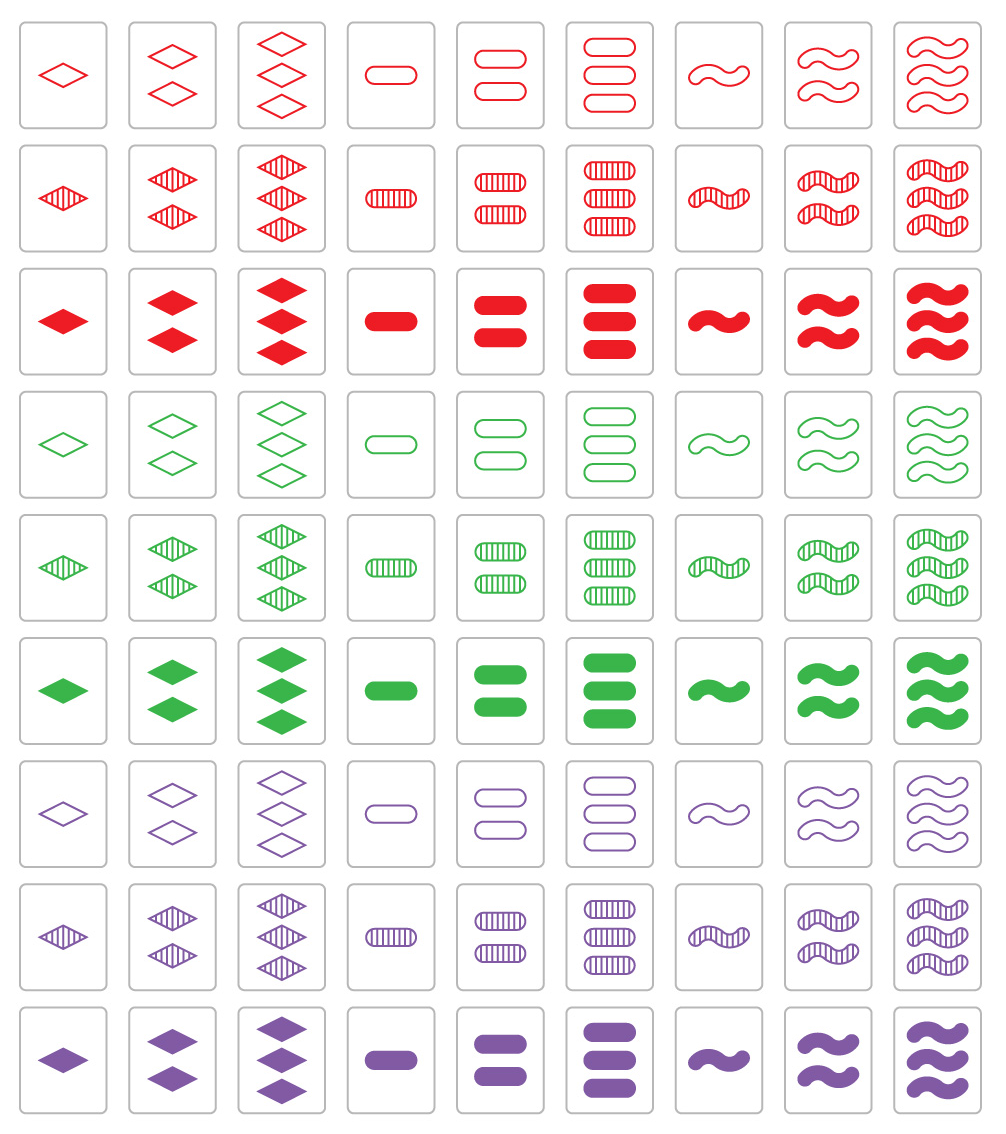
游戏集
游戏的目的是在81张纸牌中找到特殊的三张纸牌或“套”。每张卡都有自己的图形,具有四个属性-颜色(红色,紫色,绿色),形状(椭圆形,菱形,波浪形),阴影(轮廓,条纹,完全填充)和形状数(一个,两个或三个)。在正常游戏中,桌上面朝上分发12张牌,玩家寻找三张牌的集合,其中四个属性中的每一个对于所有牌都是相同的,或者对于所有牌都是不同的。如果12张卡中没有这样的卡组,则会添加更多卡。
整个甲板
, –
| ? |  |
 |
 |
 |
一种构建相当多的不包含三胞胎的卡的简单方法是,只取每个属性只有两个或三个选择的卡。此集合的大小为整个卡片组的(2/3)n,其中n是属性数。

这个问题(不仅与标准的Set游戏有关,而且与它的较大版本有关)是研究有关整数的相应问题的自然模型。因此,数学家希望Bateman和Katz的突破能够为证明Erd猜想开辟道路,特别是与其他近期突破结合时。在Bateman和Katz的作品发行后不久,高尔斯(Gowers)发起了“ polymath project“ -一个庞大的联合协作的目的是这样的尝试。
但是,该项目很快陷入停滞”在这里面聚集了大量的技术参数量, -他说高尔斯-这个项目是比较适合一两个人,很长一段时间,就可以慢慢的工作。”
通过幸运的是,有几位数学家正在为此做准备,布鲁姆和西萨斯克最初分别已经开始考虑Erd的假设,并被其中所用技术的美丽所迷住。“这是我面临的第一个研究问题,”西萨斯克说,与Bloom一样,他现在大约35岁。
Bloom和Sisask于2014年合并,到2016年,他们决定接近解决方案。布卢姆甚至在演讲中宣布了这一点,只有在此之后,他才发现他们发现的一些变通办法是错误的。这对夫妇继续工作,深入研究Bateman和Katz的方法,并最终意识到什么新思想将使他们将这种方法从Seth领域转移到整数领域。
卡茨说,这项新工作从各个角度看来都是正确的。 “我不相信他们以前的说法,但我确实相信这一点。”
福克斯说,布鲁姆和萨萨斯克的工作是“巨大的成就”。他们和其他数学家急于寻找新工作中的技术是否适用于其他问题。 “我认为这些方法将对数学产生巨大影响,”福克斯说。
至于鄂尔多斯的全部假设,还远没有完成。 Bloom和Sisask证明了该假设仅适用于等间隔的三元组,而不适用于较长的算术级数-此任务仍然遥不可及。
而且,在许多数学家看来,即使Bloom和Sisask已经解决的三分法问题也没有特别的帮助。要证明Erds密度保证等距三元组的难度是困难的,数学家怀疑此保证停止起作用的实际密度要低得多-可能比Berend设计的集合的密度稍高。
“这并不是说我们已经完全解决了这个问题,”布卢姆说。 “我们更加了解了她。”
Fox说,Bloom和Sisask可能从当前方法中挤出了最好的方法。他说:“应该有一些全新的工具,使我们能够进一步发展并取得显着更好的结果。” 但是,“这可能还不是故事的结局。”