哈Ha
在本文中,我想谈谈信息技术在地球科学中的应用主题,即水文学和制图学。切口下方是对流排名算法和我们为开放式地理信息系统QGIS实现的插件的描述。
介绍
当前,水文学研究的一个重要方面不仅是实地观察,还包括水文数据的办公室工作,包括使用GIS(地理信息系统)。但是,由于数据量大,研究水文系统的空间结构可能很困难。在这种情况下,您不能不使用允许专家使过程自动化的其他工具。
当使用数字数据,尤其是数字数据,尤其是水文数据时,可视化发挥了重要作用-正确,直观地呈现分析结果。为了在古典制图法中显示水道,采用以下方法:用实线描绘河流,并从源头到河口逐渐加深(取决于流入河流的支流的数量)。此外,对于河网的各个部分,通常需要从源头到距离进行一些排名。这种信息不仅从可视化的角度来看很重要,而且适合于更完整地了解数据结构,其空间分布以及正确的后续处理。
对河道进行排名的任务可以如下所示(图1):

图1.对河道进行排名的任务,数字表示分配给河网各段的流入支流总数的属性
因此,河流的每个部分都需要匹配一个值,该值应显示有多少部分共同流入该部分。
, ArcGIS open-source QGIS, . , , , , . , - . , , , (OpenStreetMap, Natural Earth, ).
, , , .
— . QGIS — "Lines Ranking". QGIS, GitHub.
为了使插件正常工作,需要QGIS版本> = 3.14,以及以下依赖项:Python编程语言库-networkx和pandas。
, (Line, MultiLine). , .
- “fid”. GRASS — v.clean — , .
(Start Point Coordinates), . , , , QGIS. , ( ).
: , , .
: . — , . , , . , , . . .
— , , .
, . / , .. , .. (. 2), , ..
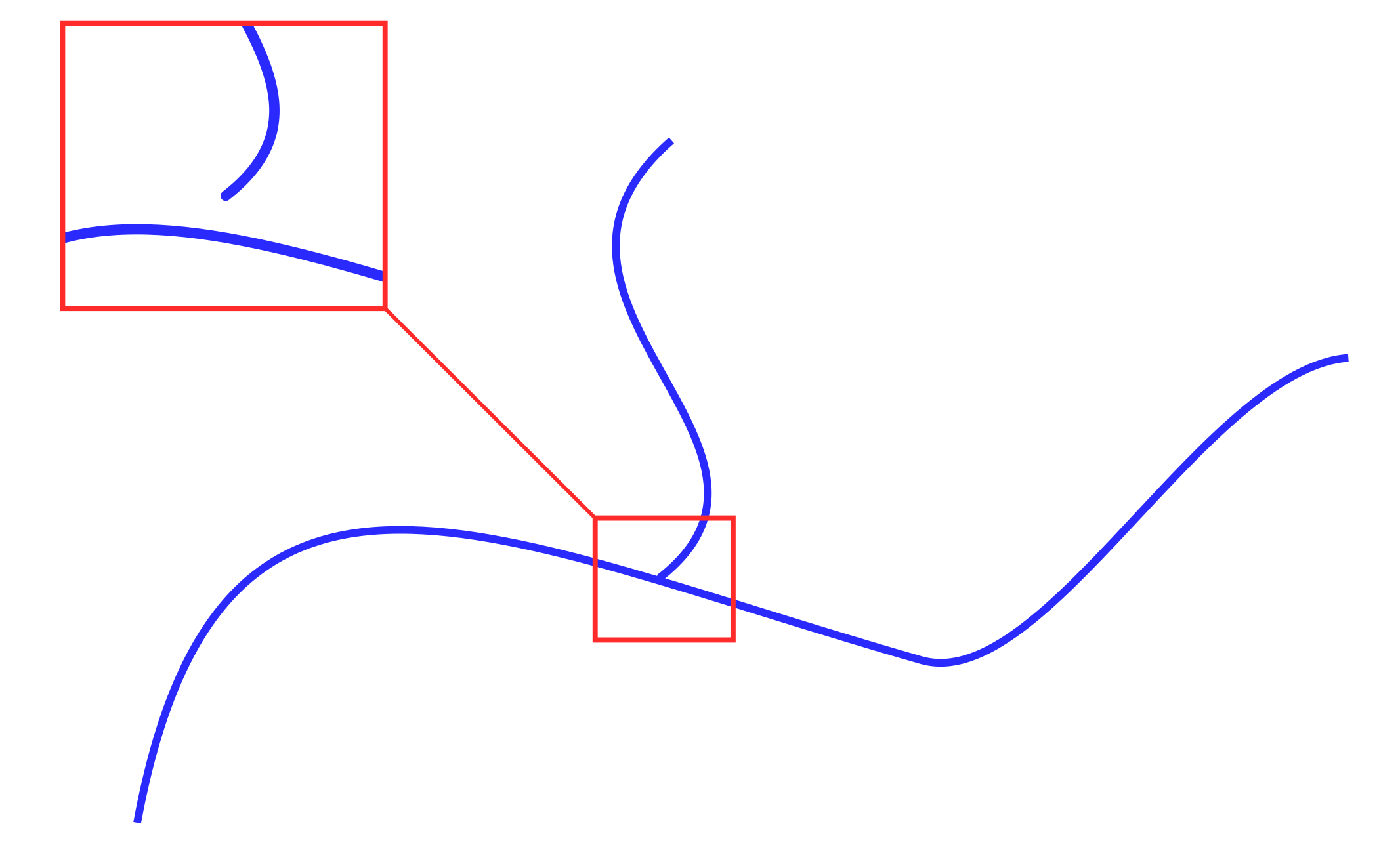
2.
: ““ , . QGIS – “ ” (fixgeometries — ) v.clean ( GRASS).
, . (. 3).

3.
, QGIS " " (splitwithlines — ) .
QGIS (. 4). ( -> -> -> ).

4.
" " (lineintersections — ) , . .
(. 5).

5.
Python networkx. , — , ( ), .
, , , ( ). , , "" (). :
- "rank" ( ) "offspring" ( );
- "value" "distance" ( ).
, , .
"rank" "offspring"
— . , "rank" . , , , , . ( )

? , , .
: - ( ), . (. 6).

6.
, 1 , — .
— ? — , , , — ( , , , ). A* (A-star), , . ( ).
1) . . . (. 7)

7.
, "length", . , .
Input:
- G —
- start — ,
- dataframe — pandas , 2 : id_field ( /) 'length' ( )
- id_field — dataframe,
- main_id — , ( = None)
Output:
- , 1, : 2 3, 'length' 1 — 10, 2 — 15, 3 — 20. : (1, 2) (2, 1) — 15; (1, 3) (3, 1) — 20 ..
- last_vertex — ( )
# Function for assigning weights to graph edges
def distance_attr(G, start, dataframe, id_field, main_id = None):
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source=start))
# One of the most remote vertices in the graph (this will be necessary for A*)
last_vertex = vert_list[-1][-1][0]
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
dist_vertex = int(dataframe['length'][dataframe[id_field] == vertex])
# Assign the segment length value as a vertex attribute
attrs = {vertex: {'component' : 1, 'size' : dist_vertex}}
nx.set_node_attributes(G, attrs)
for n in neighbors:
# If the main index value is not set
if main_id == None:
# Assign weights to the edges of the graph
# The length of the section in meters (int)
dist_n = int(dataframe['length'][dataframe[id_field] == n])
# Otherwise we are dealing with a complex composite index
else:
# If the vertex we are at is part of the main river
if vertex.split(':')[0] == main_id:
# And at the same time, the vertex that we "look" at from the vertex "vertex" also, then
if n.split(':')[0] == main_id:
# The weight value must be zero
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
# Assign attributes to the nodes of the graph
attrs = {n: {'component' : 1, 'size' : dist_n}}
nx.set_node_attributes(G, attrs)
# Look at the surroundings of the vertex where we are located
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
offspring = offspring[0][1]
# If the weight value was not assigned, we assign it
for n in offspring:
if len(G.get_edge_data(vertex, n)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
elif len(G.get_edge_data(n, vertex)) == 0:
##############################
# Assigning weights to edges #
##############################
if main_id == None:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
if vertex.split(':')[0] == main_id:
if n.split(':')[0] == main_id:
dist_n = 0
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
else:
dist_n = int(dataframe['length'][dataframe[id_field] == n])
attrs = {(vertex, n): {'weight': dist_n},
(n, vertex): {'weight': dist_n}}
nx.set_edge_attributes(G, attrs)
##############################
# Assigning weights to edges #
##############################
for vertex in list(G.nodes()):
# If the graph is incompletely connected, then we delete the elements that we can't get to
if G.nodes[vertex].get('component') == None:
G.remove_node(vertex)
else:
pass
return(last_vertex)
# The application of the algorithm
last_vertex = distance_attr(G, '7126:23', dataframe, id_field = 'id', main_id = '7126')2) A* (-star) ( ). "";
3) . , , 1, — 2, — 3 ..
4) . , , , .
Input:
- G —
- start — ,
- last_vertex —
Output:
- . 1 , . 2 , 1. 3 , 2 .. , 'rank', 'offspring'. 'offspring' ' , '.
# Function for assigning 'rank' and 'offspring' attributes to graph vertices
def rank_set(G, start, last_vertex):
# Traversing a graph with attribute assignment
# G --- graph as a networkx object
# vertex --- vertex from which the graph search begins
# kernel_path --- list of vertexes that are part of the main path that the search is being built from
def bfs_attributes(G, vertex, kernel_path):
# Creating a copy of the graph
G_copy = G.copy()
# Deleting all edges that are associated with the reference vertexes
for kernel_vertex in kernel_path:
# Leaving the reference vertex from which we start the crawl
if kernel_vertex == vertex:
pass
else:
# For all other vertexes, we delete edges
kernel_n = list(nx.bfs_successors(G_copy, source = kernel_vertex, depth_limit = 1))
kernel_n = kernel_n[0][1]
for i in kernel_n:
try:
G_copy.remove_edge(i, kernel_vertex)
except Exception:
pass
# The obtained subgraph is isolated from all reference vertices, except the one
# from which the search begins at this iteration
# Breadth-first search
all_neighbors = list(nx.bfs_successors(G_copy, source = vertex))
# Attention!
# Labels are not assigned on an isolated subgraph, but on the source graph
for component in all_neighbors:
v = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Value of the 'rank' attribute in the considering vertex
att = G.nodes[v].get('rank')
if att != None:
# The value of the attribute to be assigned to neighboring vertices
att_number = att + 1
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = v, depth_limit = 1))
first_n = first_n[0][1]
# Assigning ranks to vertices
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
current_i_rank = G.nodes[i].get('rank')
# If the rank value has not yet been assigned, then assign it
if current_i_rank == None:
attrs = {i: {'rank': att_number}}
nx.set_node_attributes(G, attrs)
# If the rank in this node is already assigned
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(v, i)
else:
pass
# Additional "search"
for neighbor in neighbors:
# We look at all the closest first offspring
first_n = list(nx.bfs_successors(G, source = neighbor, depth_limit = 1))
first_n = first_n[0][1]
for i in first_n:
# If the neighboring vertex is the main node in this iteration, then skip it
# vertex - the reference point from which we started the search
if i == vertex:
pass
else:
# The algorithm either "looks back" at vertices that it has already visited
# In this case we don't do anything
# Either the algorithm "came up" to the main path (kernel path) in the graph
if any(i == bearing_v for bearing_v in kernel_path):
G.remove_edge(neighbor, i)
else:
pass
# Finding the shortest path A* - building a route around which we will build the next searchs
a_path = list(nx.astar_path(G, source = start, target = last_vertex, weight = 'weight'))
##############################
# Route validation block #
##############################
true_a_path = []
for index, V in enumerate(a_path):
if index == 0:
true_a_path.append(V)
elif index == (len(a_path) - 1):
true_a_path.append(V)
else:
# Previous and next vertices for the reference path (a_path)
V_prev = a_path[index - 1]
V_next = a_path[index + 1]
# Which vertexes are adjacent to this one
V_prev_neighborhood = list(nx.bfs_successors(G, source = V_prev, depth_limit = 1))
V_prev_neighborhood = V_prev_neighborhood[0][1]
V_next_neighborhood = list(nx.bfs_successors(G, source = V_next, depth_limit = 1))
V_next_neighborhood = V_next_neighborhood[0][1]
# If the next and previous vertices are connected to each other without an intermediary
# in the form of vertex V, then vertex V is excluded from the reference path
if any(V_next == VPREV for VPREV in V_prev_neighborhood):
if any(V_prev == VNEXT for VNEXT in V_next_neighborhood):
pass
else:
true_a_path.append(V)
else:
true_a_path.append(V)
##############################
# Route validation block #
##############################
# Verification completed
a_path = true_a_path
RANK = 1
for v in a_path:
# Assign the attribute rank value - 1 to the starting vertex. The further away, the greater the value
attrs = {v: {'rank' : RANK}}
nx.set_node_attributes(G, attrs)
RANK += 1
# The main route is ready, then we will iteratively move from each node
for index, vertex in enumerate(a_path):
# Starting vertex
if index == 0:
next_vertex = a_path[index + 1]
# Disconnect vertices
G.remove_edge(vertex, next_vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(vertex, next_vertex)
# Finishing vertex
elif index == (len(a_path) - 1):
prev_vertex = a_path[index - 1]
# Disconnect vertices
G.remove_edge(prev_vertex, vertex)
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
G.add_edge(prev_vertex, vertex)
# Vertices that are not the first or last in the reference path
else:
prev_vertex = a_path[index - 1]
next_vertex = a_path[index + 1]
# Disconnect vertices
# Previous with current vertex
try:
G.remove_edge(prev_vertex, vertex)
except Exception:
pass
# Current with next vertex
try:
G.remove_edge(vertex, next_vertex)
except Exception:
pass
# Subgraph BFS block
bfs_attributes(G, vertex = vertex, kernel_path = a_path)
# Connect vertices back
try:
G.add_edge(prev_vertex, vertex)
G.add_edge(vertex, next_vertex)
except Exception:
pass
# Attribute assignment block - number of descendants
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# Adding an attribute - the number of descendants of this vertex
n_offspring = len(neighbors)
attrs = {vertex: {'offspring' : n_offspring}}
nx.set_node_attributes(G, attrs):

, , . .
, "" , , , , , .
"value" "distance"
, "rank" "offspring". .
, , , , "value" — 1. , , "value", 1, "value" ( 1 , ) "value". , , .
, .
Input:
- G — 'rank' 'offspring'
- start — ,
Output:
- G 'value'. ' '. 'distance', , , .
# Function for determining the order of river segments similar to the Shreve method
# In addition, the "distance" attribute is assigned
def set_values(G, start, considering_rank, vert_list):
# For each vertex in the list
for vertex in vert_list:
# If value has already been assigned, then skip it
if G.nodes[vertex].get('value') == 1:
pass
else:
# Defining descendants
offspring = list(nx.bfs_successors(G, source = vertex, depth_limit = 1))
# We use only the nearest neighbors to this vertex (first descendants)
offspring = offspring[0][1]
# The cycle of determining the values at the vertices of a descendant
last_values = []
for child in offspring:
# We only need descendants whose rank value is greater than that of the vertex
if G.nodes[child].get('rank') > considering_rank:
if G.nodes[child].get('value') != None:
last_values.append(G.nodes[child].get('value'))
else:
pass
else:
pass
last_values = np.array(last_values)
sum_values = np.sum(last_values)
# If the amount is not equal to 0, the attribute is assigned
if sum_values != 0:
attrs = {vertex: {'value' : sum_values}}
nx.set_node_attributes(G, attrs)
else:
pass
# Function for iteratively assigning the value attribute
def iter_set_values(G, start):
# Vertices and corresponding attribute values
ranks_list = []
vertices_list = []
offspring_list = []
for vertex in list(G.nodes()):
ranks_list.append(G.nodes[vertex].get('rank'))
vertices_list.append(vertex)
att_offspring = G.nodes[vertex].get('offspring')
if att_offspring == None:
offspring_list.append(0)
else:
offspring_list.append(att_offspring)
# Largest rank value in a graph
max_rank = max(ranks_list)
# Creating pandas dataframe
df = pd.DataFrame({'ranks': ranks_list,
'vertices': vertices_list,
'offspring': offspring_list})
# We assign value = 1 to all vertices of the graph that have no offspring
value_1_list = list(df['vertices'][df['offspring'] == 0])
for vertex in value_1_list:
attrs = {vertex: {'value' : 1}}
nx.set_node_attributes(G, attrs)
# For each rank, we begin to assign attributes
for considering_rank in range(max_rank, 0, -1):
# List of vertices of suitable rank
vert_list = list(df['vertices'][df['ranks'] == considering_rank])
set_values(G, start, considering_rank, vert_list)
# Assigning the "distance" attribute to the graph vertices
# List of all vertexes that can be reached from the start vertex using BFS
vert_list = list(nx.bfs_successors(G, source = start))
for component in vert_list:
vertex = component[0] # The vertex where we are at this iteration
neighbors = component[1] # Vertices that are neighboring (which we haven't visited yet)
# If we are at the closing vertex
if vertex == start:
# Length of this segment
att_vertex_size = G.nodes[vertex].get('size')
# Adding the value of the distance attribute
attrs = {vertex: {'distance' : att_vertex_size}}
nx.set_node_attributes(G, attrs)
else:
pass
vertex_distance = G.nodes[vertex].get('distance')
# For each neighbor, we assign an attribute
for i in neighbors:
# Adding the value of the distance attribute
i_size = G.nodes[i].get('size')
attrs = {i: {'distance' : (vertex_distance + i_size)}}
nx.set_node_attributes(G, attrs) 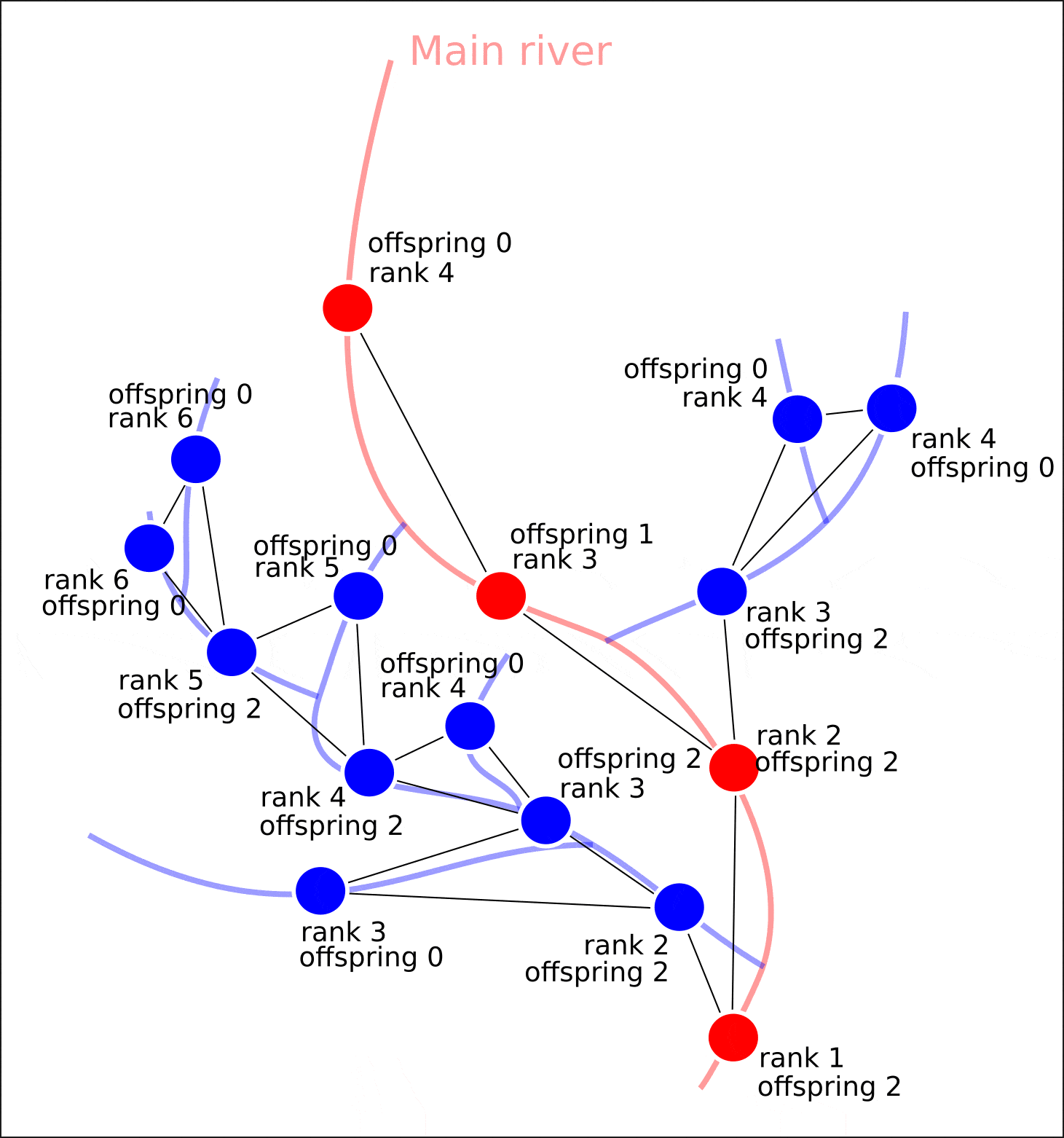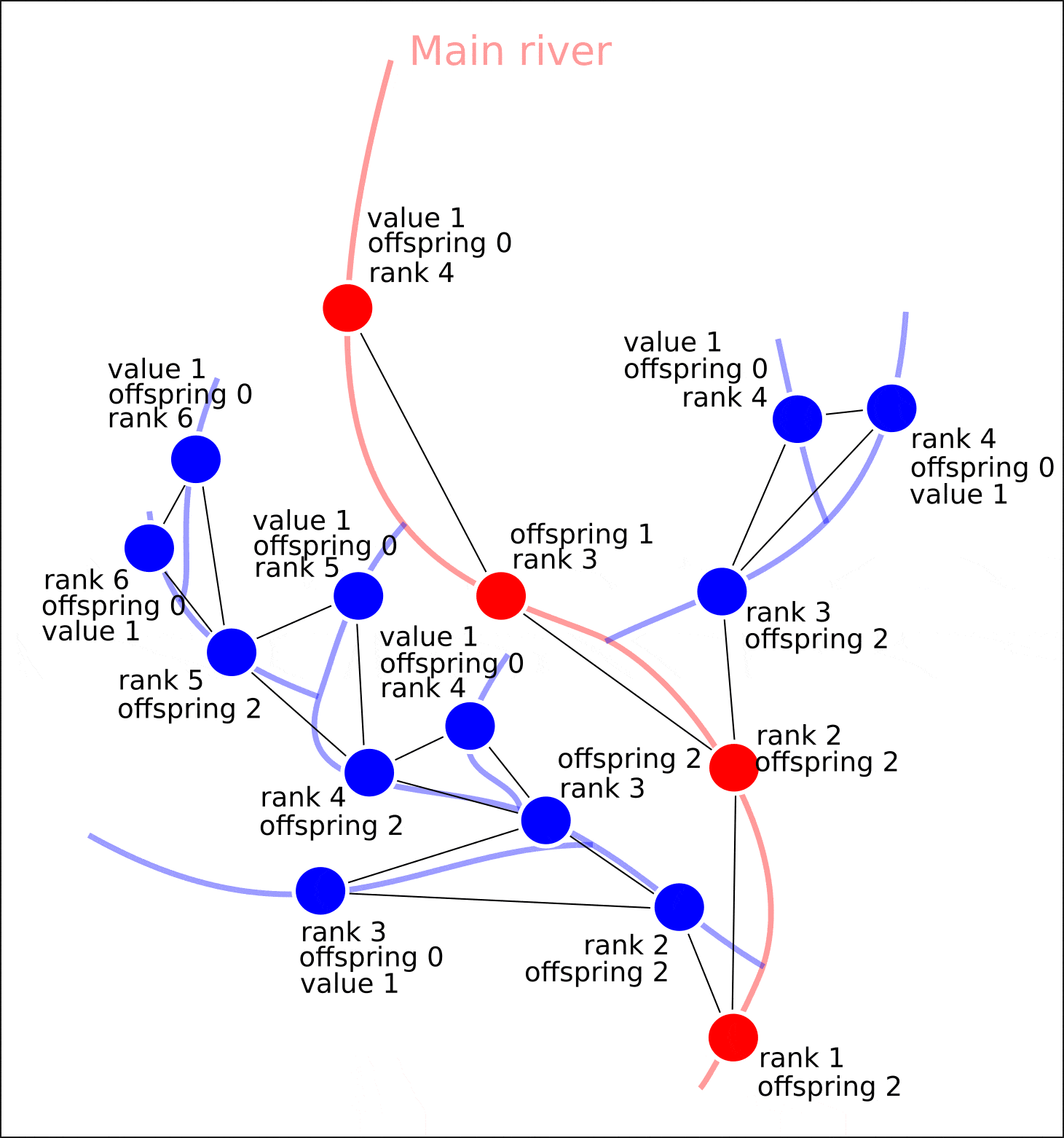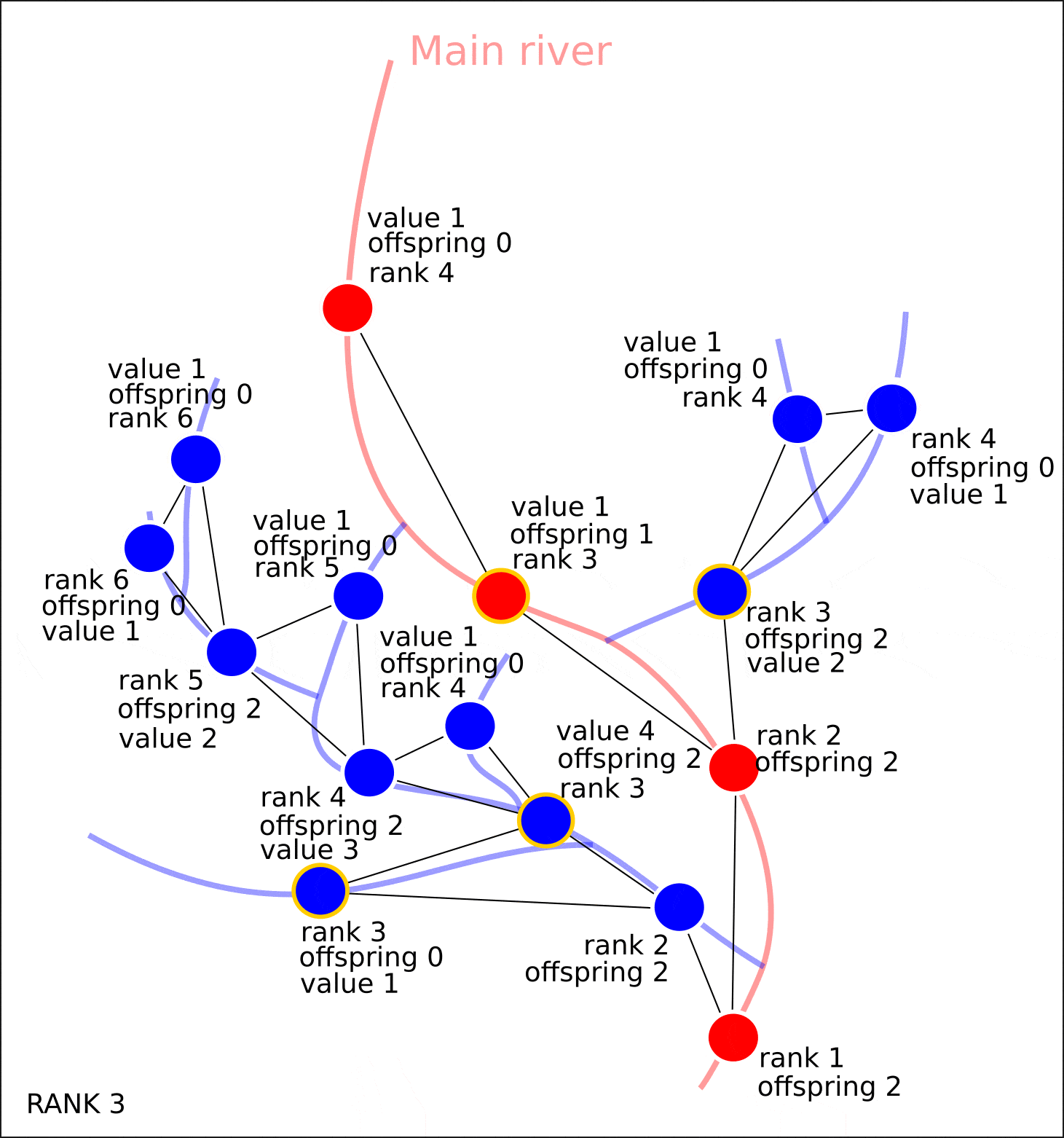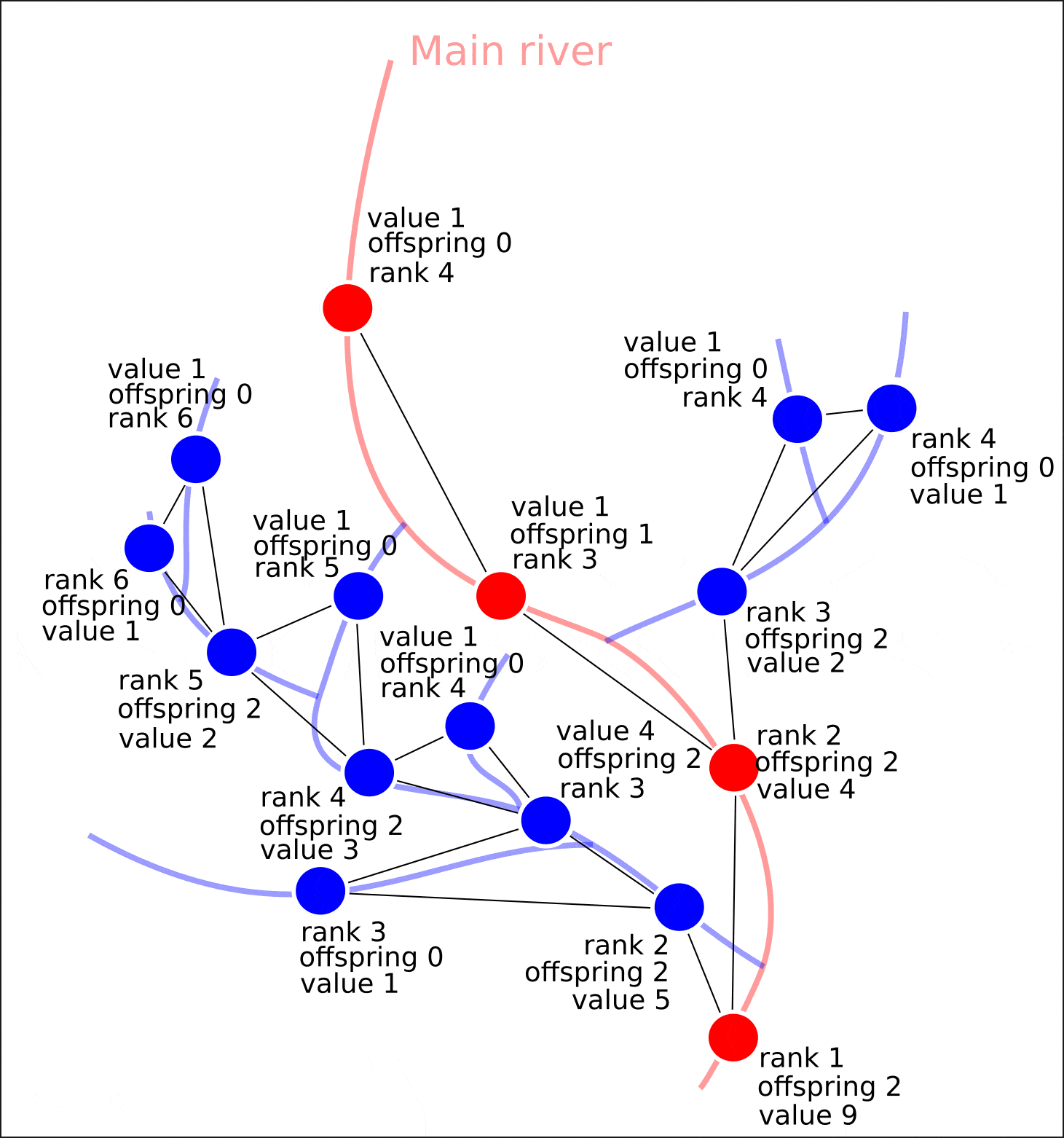
"value", "distance", , , , , , .
8. "rank" "value".

8. ( OpenStreetMap, "rank", - "value")
, . ( ), .
, , .
Python, QGIS . , .
.
源代码存储库:
Mikhail Sarafanov和Yulia Borisova负责算法和文章。