
这是一个表格(20x20),每个单元格中的整数都为0到99。
我们的任务是找到四个相邻的数字而不打断链,一个接一个,另一个具有最大乘积。4个相邻数字的不同变体用颜色突出显示(如果两个数字彼此之间的距离不超过1个,则视为两个数字相邻)。
今天,我们将在C#中实现搜索算法。
首先,让我们创建一个20x20的二维数组并将其写入文件:
static void CreateArrayFile()
{
Random random = new Random();
string file = "";
for (int i = 0; i < 20; i++)
{
string line = "";
for (int j = 0; j < 20; j++)
{
line += random.Next(0, 99) + ",";
}
line = line + Environment.NewLine;
file += line;
}
using (FileStream fstream = new FileStream($"array.txt", FileMode.OpenOrCreate))
{
byte[] array = System.Text.Encoding.Default.GetBytes(file);
fstream.Write(array, 0, array.Length);
Console.WriteLine(" ");
}
}

现在,我们可以将文件中的数字写到二维数组中。
string[] lines = arrayFile.Split(Environment.NewLine);
for (int i = 0; i < 20; i++)
{
string[] items = lines[i].Split(',');
for (int j = 0; j < 20; j++)
{
table[i, j] = Convert.ToInt32(items[j]);
}
}
让我们创建一个Element类来表示数字的坐标和值:
public class Element
{
public int Line { get; set; }
public int Column { get; set; }
public int Value { get; set; }
}
根据问题的情况,需要找到作品的组合。让我们实现Multiplication类来表示一个包含数字数组的组合以及该组合中数字乘积的值。
public class Multiplication
{
public Multiplication()
{
Elements = new Element[4];
}
public Element[] Elements { get; set; }
public int Value
{
get
{
Multiply();
return value;
}
}
int value;
void Multiply()
{
if(Elements[0] != null && Elements[1] != null && Elements[2] != null && Elements[3] != null)
{
value = Elements[0].Value * Elements[1].Value * Elements[2].Value * Elements[3].Value;
}
}
}
首先要做的是找到该数字的最近邻居。例如,对于本例中的数字40,以下邻居:
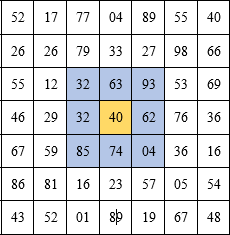
右下角的数字48只有3个邻居。不难理解,任何数目的邻居都是:
table[i-1][j-1]
table[i-1][j]
table[i-1][j+1]
table[i][j-1]
table[i][j+1]
table[i+1][j-1]
table[i+1][j]
table[i+1][j+1]
在确保索引没有超出范围之后,我们得到FindNeighbors方法,该方法返回特定数字的所有最近邻居的集合。
根据问题,我们需要找到4个相邻数字的组合。为此,我们需要一种方法来查找4个数字的所有可能组合:
static List<Multiplication> GetFactorCombinations(int line, int column)
{
List<Multiplication> combinations = new List<Multiplication>();
if (table[line, column] != 0)
{
List<Element> firstLevelNeighbors = FindNeighbors(line, column);
foreach (var firstLevelNeighbor in firstLevelNeighbors)
{
Element[] elements = new Element[4];
elements[0] = new Element
{
Line = line,
Column = column,
Value = table[line, column]
};
elements[1] = firstLevelNeighbor;
List<Element> secondLevelNeighbors = FindNeighbors(firstLevelNeighbor.Line, firstLevelNeighbor.Column);
foreach (var secondLevelNeighbor in secondLevelNeighbors)
{
if (!elements[0].Equals(secondLevelNeighbor) && !elements[1].Equals(secondLevelNeighbor))
{
elements[2] = secondLevelNeighbor;
}
if (elements[2] != null)
{
List<Element> thirdLevelNeighbors = FindNeighbors(secondLevelNeighbor.Line, secondLevelNeighbor.Column);
foreach (var thirdLevelNeighbor in thirdLevelNeighbors)
{
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var nnnn =new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(nnnn);
}
}
}
}
}
}
}
return combinations;
}
该方法获取表中数字的坐标,然后将该数字的值乘以0(将任何数字乘以0时,结果始终为0)。然后,该方法搜索给定数字的所有邻居。我们遍历第一级的邻居,如果数字不为0,我们正在寻找第二级的所有邻居...我们
重写了Equals方法来比较数字:
public override bool Equals(Object obj)
{
if (this==null || (obj == null) || !this.GetType().Equals(obj.GetType()))
{
return false;
}
else if(Line == ((Element)obj).Line && Column == ((Element)obj).Column)
{
return true;
}
else
{
return false;
}
}
我们继续搜索第四级的邻居,如果没有重复的数字,则将其添加到我们的集合中。
if (!elements[0].Equals(thirdLevelNeighbor) && !elements[1].Equals(thirdLevelNeighbor) && !elements[2].Equals(thirdLevelNeighbor))
{
elements[3] = thirdLevelNeighbor;
Multiplication multiplication = new Multiplication
{
Elements = elements
};
if (combinations.Where(p=>p.Elements[0].Value==elements[0].Value&& p.Elements[1].Value == elements[1].Value && p.Elements[2].Value == elements[2].Value && p.Elements[3].Value == elements[3].Value).FirstOrDefault()==null)
{
var combination=new Multiplication
{
Elements = new Element[] { elements[0], elements[1], elements[2], elements[3]}
};
combinations.Add(combination);
}
}
GetFactorCombinations方法可以如下所示:

现在,遍历二维数组,我们正在寻找最大的数字组合。
for (int i = 0; i < 20; i++)
{
for (int j = 0; j < 20; j++)
{
List<Multiplication> combinations = GetFactorCombinations(i, j);
foreach (var combination in combinations)
{
if (combination.Value > maxMultiplication.Value)
{
Console.WriteLine(" " + combination.Elements[0].Value + " * " + combination.Elements[1].Value + " * " + combination.Elements[2].Value + " * " + combination.Elements[3].Value + " = " + combination.Value);
maxMultiplication = combination;
}
}
}
}
Console.WriteLine(" = " + maxMultiplication.Elements[0].Value + " * " + maxMultiplication.Elements[1].Value + " * " + maxMultiplication.Elements[2].Value + " * " + maxMultiplication.Elements[3].Value + " = " + maxMultiplication.Value);
如果下一个组合大于maxMultiplication,则将其重写。
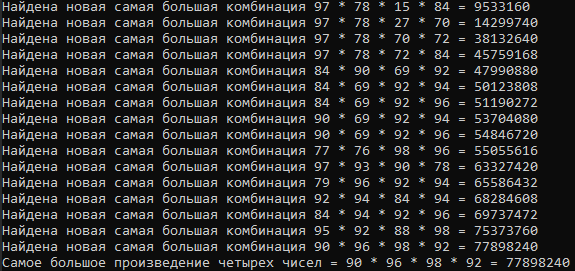
是的,我们做到了。我们发现最大的产品是4个数字的组合。
实际上,我们已经解决了问题,但是代码是针对特定条件进行硬编码的,是一种纯粹的过程方法。如果我们需要从矩阵中搜索的不是20 x 20,而是30 x 30,而不是4,而是5个数字的组合?每次添加另一个嵌套循环(以全部迭代)...我们
为表的大小以及所需组合的大小保留2个常量:
const int TABLE_SIZE = 20;
public const int COMBINATION_SIZE = 4;
让我们将GetFactorCombinations方法重写为递归方法:
static List<Multiplication> GetMultiplicationForStep(int line, int column, List<Element> otherElements = null)
{
List<Multiplication> resultMultiplications = new List<Multiplication>();
List<Element> resultElements = new List<Element>();
Element element = new Element
{
Column = column,
Line = line,
Value = table[line, column]
};
if (otherElements == null)
{
otherElements = new List<Element>();
}
if(otherElements!=null)
{
resultElements.AddRange(otherElements);
}
if (table[line, column] != 0)
{
if (otherElements.Where(p => p.Equals(element)).FirstOrDefault() == null)
{
resultElements.Add(element);
}
}
if (resultElements.Count() == COMBINATION_SIZE)
{
Multiplication multiplication = new Multiplication
{
Elements = resultElements.ToArray()
};
resultMultiplications.Add(multiplication);
}
else
{
List<Element> elementNeighbors = FindNeighbors(line, column);
elementNeighbors = elementNeighbors.Where(p => !p.Equals(element)&& otherElements.Where(p=>p.Equals(element)).FirstOrDefault()==null).ToList();
List<Multiplication> newMultiplications = new List<Multiplication>();
foreach(Element neighbor in elementNeighbors)
{
// COMBINATION_SIZE ...
newMultiplications.AddRange(GetMultiplicationForStep(neighbor.Line, neighbor.Column, resultElements).Where(p=>p!=null));
}
foreach(Multiplication multiplication in newMultiplications)
{
if(resultMultiplications.Where(p=>p.Value==multiplication.Value).FirstOrDefault()==null)
{
resultMultiplications.Add(multiplication);
}
}
}
return resultMultiplications;
}
该方法按照与以前相同的原理工作,但是代替嵌套循环,我们递归地继续搜索邻居,直到找到的元素数为resultElements.Count()!= COMBINATION_SIZE
找到组合后,您可以在控制台中漂亮地显示它:
for (int i = 0; i < TABLE_SIZE; i++)
{
for (int j = 0; j < TABLE_SIZE; j++)
{
if (maxMultiplication.Elements.Where(p => p.Line == i && p.Column == j).FirstOrDefault() != null)
{
Console.BackgroundColor = ConsoleColor.White;
Console.ForegroundColor = ConsoleColor.Black; // ,
Console.Write(table[i, j] + " ");
Console.ResetColor();
}
else
{
Console.Write(table[i, j] + " ");
}
}
Console.WriteLine();
}
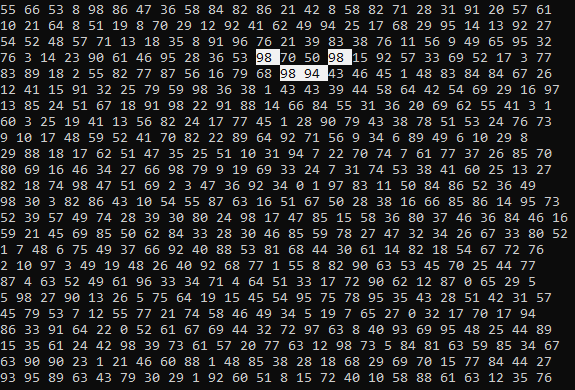
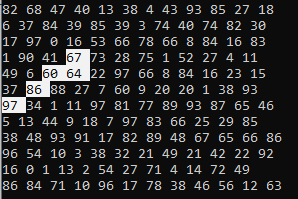
结论
在本文中,我们熟悉了在NxN表中查找相邻组合的选项之一。
你还能做什么:
- 您可以考虑摆脱所有组合的多次迭代,并以其他方式优化代码。
- 基于现有算法,在3维数组上实现对相邻数字组合的搜索。但这已经是另一次了...
