🥇 👧🏾 🏽 编码和加密的数学基础 🤵🏽 ⛽️ 👨🏻‍🌾

用户在计算机和通信网络中的信息交互会受到各种干扰，从而导致各种错误和干扰。除了所发送的消息中的错误外，还可以对犯罪者的消息的内容进行未经授权的访问。与这些不良现象的斗争已经进行了数千年，但取得了不同的成功。互联网的创造者并没有完全按照现在的方式来构想它。那时他们甚至都没有考虑过黑客。

信息对抗的主要理论问题及其解决任务被分配到密码学，密码学和隐写学的理论中，在全世界密码学分析，密码学分析和隐写分析的方向正在深入发展。实践方面也不能忽略，但我要指出的是，俄罗斯联邦的活动不是很高，受年轻人的惯性影响（我本人已经交换了第九个十年，但是哈勃政府在1950年限制了年龄限制）。当然，我的意见仅限于观察后代（最多曾孙）和通过Internet交流，以及与我兼职的公司的受训人员和员工交流。媒体也增加了负面影响。一些年轻人变得更聪明了，越过山坡。您可以自己查看其他人的行为。

导览出版物

技术设备的开发（综合）需要开发人员一定的知识，使用它们的能力以及其他此类技能。这种知识的基本组成部分是数学。通常，这些是代数，离散数学，几何，物理学，数学逻辑等。在本文中，我们将不完全考虑经典表示中的代数结构，但要具有足够的严格性和准确性。我的主要任务是确保我在课本和研究中使用的事物的表达方式的可访问性和清晰度。

例如，此处使用GF扩展字段（2 ⁸），如果我们不这样做，那么就没有什么值得一提的了。我的评估标准很简单。每个学期进行2次，甚至在不同的学习小组中进行3次考试和测验。在那儿，我听到并看到了我阐述，付诸实践的内容以及考试卡上的答案所返回的内容。考试答案的分析非常有用，我认为应该以不同的方式更好地陈述。

而这里的性能ž _ñ对N的有限数值残差环求模N = pq用于在新的原始方法的框架内找到分解大数的问题的解决方案。显然，在随后的每个出版物中，都没有必要转让部分标准数学工具，因此，决定将所有内容都集中在一个地方，并在必要时在此处与读者联系。

这里考虑并使用了平面上的椭圆曲线的一组点。组中的求和操作是一种非常特殊的操作，会引起一些令人困惑的问题，例如，即使从HEC成员中，您如何设法添加曲线的点。

团体

让我们首先介绍一些必要的定义。

定义。有限集A集，任意n个对象的集合

a_{1}, a_{2}, . . ., a_{n}

${a_1,a_2,..., a_n}$ ，以任何顺序列出的，但其中不存在重复。可以对集合进行结构化（如果未指定任何操作），则可以在其元素上指定一个（或多个）操作和关系；也可以对结构进行非结构化。

下面，作为提醒，与有限的离散集合的动作（操作）的表中给出，并且为了清楚起见，图中还显示连续集合A和B

的操作的表用套

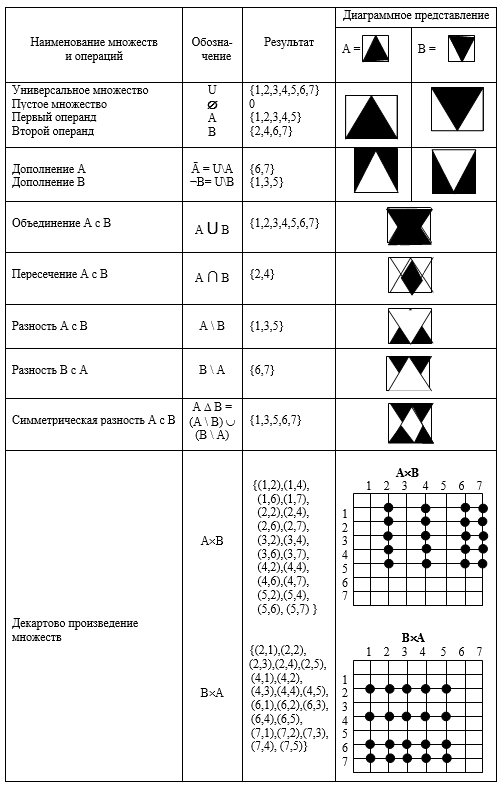
定义。运算是映射A×A→A或例如a·b = c； a，b，c ∊ A.算术以外的代数结构也被考虑：一元（例如，反演b ^-1），二元，三元，...，n元（根据操作数的位数）或乘法排列，模块化（通过（mod R）获得结果）等。如果ab = ba，则称元素a和b进行置换或交换。

定义。一组是一组G元素（具有任意性质），在其上指定了一个操作，但可以是加号（+），该组称为加法运算，其中性元素（0）或乘法（◦）称为乘法运算，其中性元素（1），但通常这些运算不是普通的算术运算，而是特殊的运算。该组通常用符号（G，◦）表示；在所有组中，对称组都占有重要位置

S_{n}

$S_n$ 个排列。保留组属性的组元素部分称为子组。本质上，这些是相同的组，仅比原始组小。这是一个非正式的组定义，稍后将给出正式的定义。

对所有a，b都满足交换定律ba = ab的G组被称为数学家Abel（1802 -1829）Abelian。

加法组的一个示例是汉明码中的一组单词（请参阅此处））。该组中的操作为16阶-单词的总和为（mod2）。使用该组，执行由代码的子组分解为128个单词的组的连续类的操作，还构造了Keli表，该组的元素用于编码器（维数为4的空间的基础）和解码器中。总之，该示例清楚地说明了即使是一小群人也可以用来解决非常重要的实际问题（交流）。

对称置换（置换）群在群论中非常重要。该重要性由定理确定，该定理说，对于在任意主题区域中出现的任何组，在排列上都有一个与它同构的对称组（子组）。然后，对于一个新的开放小组的研究人员来说，研究它的任务得以简化。同构置换组的几乎所有属性在新组中均有效。

让我们从一个简单的例子开始。给出了N个元素（我们用数字1,2,3，...，n表示），并根据它们形成排列，其数目为n！ = 1 2 3 ... n。让我们将自己限制为n = 3，然后是3！ = 6.

定义。组顺序-组中元素的数量称为其顺序。在示例中，数字6是组的顺序。

在组中，每个元素还具有一个顺序，该顺序是该组顺序的除数。

定义。组元素的阶数是乘法组中元素的最小指数（加性b + b + b + b + ... b = nb = 0，阶数= n），在该处它成为中性元素，例如（

р_{4}

$_4$ ）³= 1，命令ord（

р_{4}

$_4$ ）=3。

在对称组中

S_{n}

$S_n$ 运算是排列的乘积。此乘法与矩阵乘法相似，因为度n的每个置换都与一个n×n正方形置换矩阵相关联，其中每个行和列都包含一个单位。对称组如下所示

S_{3}

$S_3$ 。

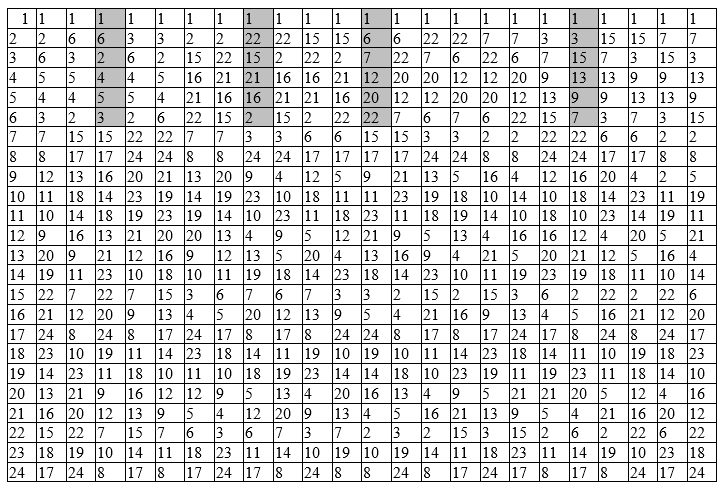
为了方便与小组及其元素合作，数学家Keli提出了小组行动表（规模有限）。在行和列相交处的单元格中，放置具有表示它们的元素的运算结果。表中的结果（以及行/列的指定）由十进制元素编号表示，从而节省了空间。

一组元素（排列）的乘法表

S_{3}

$S_3$

通过使用Keli表的属性，可简化对乘法表的36个单元格的填充。

-所有行和列都包含整个组的元素。

-极端列按字典顺序排序，并且方向相反（第一个顶部/底部，最后一个则相反）

-在表格的主对角线上有元素的平方，如果有1，则对应的元素是对合；内卷

S_{3}

$S_3$ 是

р_{1}, р_{2}, р_{3}, р_{6}

$_1,_2,_3,_6$

相对于矩阵的对角线实现元素位置的对称性。

该表的属性允许在填充表时将计算限制为仅13对元素（如上所示）。

对称组 $S_4$

组

S_{3}

$S_3$ 的阶数较小（6），并且对于说明性质不是很方便。下面我们将以对称组为例

S_{4}

$S_4$ 24订单。次数n的所有偶数排列在对称组中形成一个交替子组，用符号A_n表示。

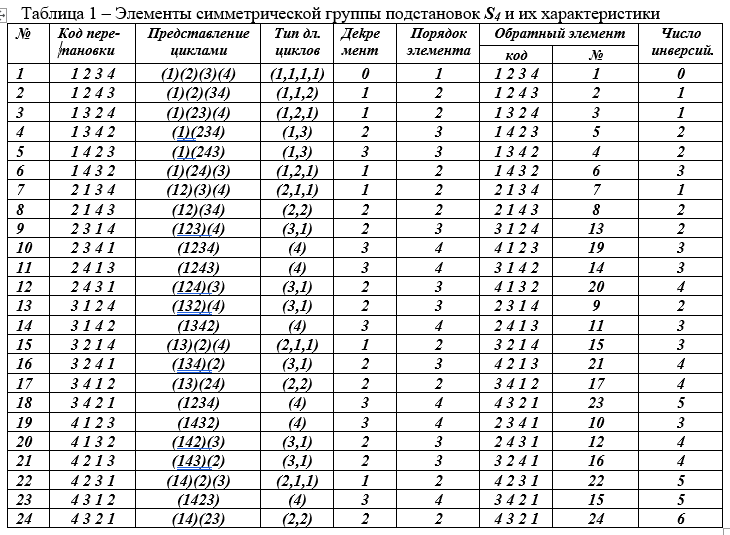
表2可用于查找任何一对元素的乘积

S_{4}

$S_4$ 或它们的整个链，但通过将结果与下一个元素顺序相乘来找到。您无法重新布置作品中的元素。与矩阵乘法一样，乘法排列的运算不是可交换的。一个元素乘以多次直到获得1，就形成了所有中间结果的循环组。这种循环子组的顺序是生成器的顺序；它必须除以原始大组的顺序。

根据乘法表，一个大组中有子组。请记住，较小子组的顺序必须除以较大子组的顺序。

我们构造一个循环群，元素p₁₄产生。我们输入表2。在第14行中，我们找到与p₁₄的交点。列元素p ₂₄ ; 在第24行中，我们在与列14相交的单元格中找到元素p ₁₁，最后在与列14相交的第11行的单元格中找到元素p ₁，即中性元素1。因此，p ₁₄ ·p ₁₄ ·p ₁₄ ·p ₁₄ = p ₁，它们是4阶子组的元素，其值完全除以24：4 = 6的阶数。为此，您可以构造Keli表，但不能在该子组中，元素p ₁₄和p ₁₁具有第4阶，而元素p _24第2阶是对合。

组态射

如果对于任何a，b ∊ G，f（a * b）= f（a）◦f（b），则将组（G，*）映射到组（G'，◦）的f称为同态（或同态）。通常，这些等式继续为f（e）= e'，

f（a ^-1）=（f（a））- ¹。等式右边的符号表示图像，称为图像；左边的符号f的原图。在一般情况下，对图像和原图像的操作不一致。同态f下的恒等式（G'，◦）的逆像称为该同态的核，用ker f表示。学年中一个著名的例子是这样的映射

日志（a◦b）=日志（a）+日志（b）。

图像元素上有一个运算符（+），在原图像中，这些元素通过乘法运算（◦）连接在一起。组的同态图像是一个组（子组），即，如果G在G'上的f同态且G是一个组，则G'也是一个组。同构是群同构的一般化：如果f是G到G'的一对一同构映射，则它是同构的，记为G≈G'。

如果存在映射f，则两个具有操作（·）和（*）的G和G组称为同构：G→G'使得图像（映射f保留了组操作）；

定理。令H为G组的一个正常子组，G = G /H。然后，由公式f（a）= a给出的群G到g的映射f是同态的。这种同态的核心是H。这种同态通常被称为自然（规范）。

规范同态基本上耗尽了组同态。

让我们将关于其子组H = {1,8，17,24}的第24阶的组G分解为陪集，并为该分解构造关于子组H的商组。为此，我们在列中写入子组H的元素的左右乘积。

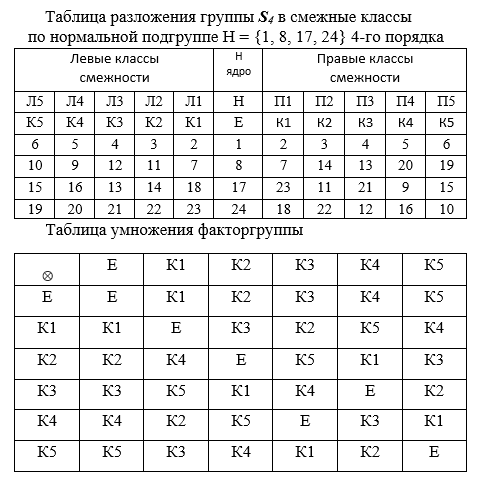
在将相对于子组H的第24阶G组分解为陪集的表中，第l1，l2，l3，l4，l5列指定为左名称，而n1，n2，n3，n4，n5-右陪集的名称写成该类的前导代表，每列一个。下一行。

中间的列H是四阶组（同构的核）。这些列中填充了班级的主要代表和H组元素的乘积。填写完列后，将对这些类进行比较。如果左右类别的组成重合，则它们仅涉及陪集类别，并表示H = K0，K1，K2，K3，K4，K5。此外，子组H称为normal。填写表格时，下一类的主要代表从那些尚未包含在已构建类中的元素中选择最小的元素G。

所获得的陪集还被视为新组的元素，该新组称为子组H的组G的商组（表示商组G = G / H）。这个新组中的操作是类的乘积：对于每对类，例如K3×K5 = K2，将构造一个4×4表，其中表行标有第一个因子的元素，而列则标有-第二个元素。此外，与组G一样进行乘法。这种乘法的结果给出了16个元素，但它们都属于同一类，在我们的情况下为K2类。

除了同构映射之外，同构是内同构和自同构。组G与其自身的同态被称为内同态，而组G与其自身的同构被称为自同构。这些概念与通过注入，排斥和双射的非结构化集合图的概念可比。

表2-Keli对称群 $$ inline $ S_4（乘法P_k = P_i P_j）$ $内联$

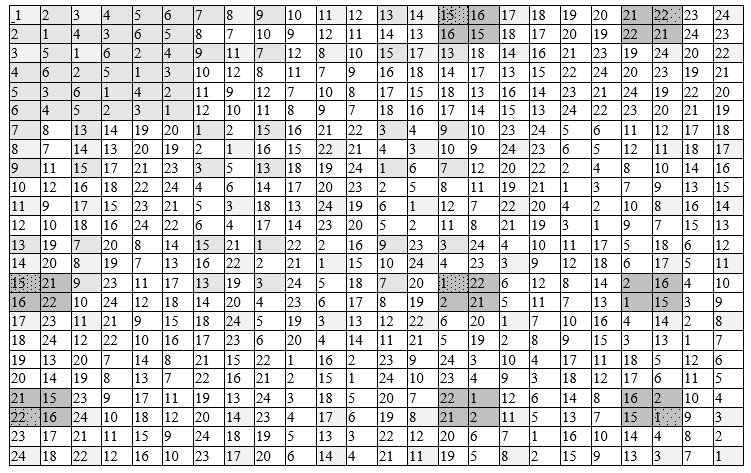
换向器

对于每对元素a，b ∊ G，我们将一个称为该对换向器的元素

[a，b] = a ^-1 b ^-1 ab关联。由其所有换向器产生的组G的子组K被称为组G的换向器子组或派生子组。

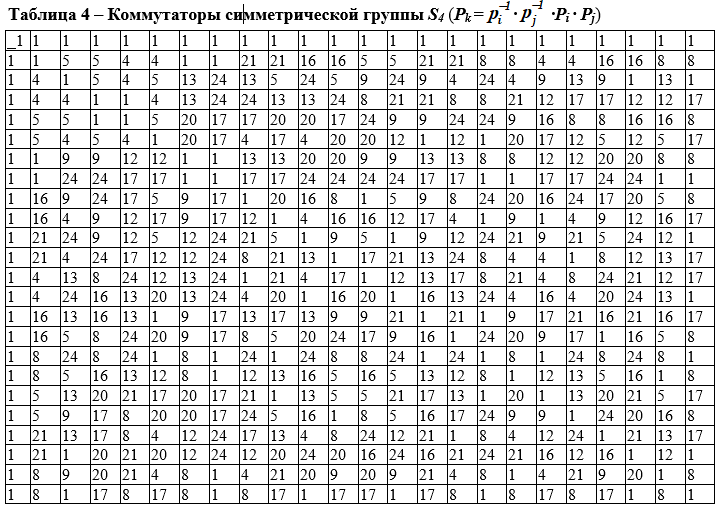
如果链G⊇G'⊇G''⊇…⊇G ^（i） ⊇...（其中每个子组G ^（i）是上一个子交换子^）在单元子组上经过有限步数后终止，则称G组为可解。^（f） =1。

在表4中，交替子组G'= 12的A ₄是正常的，从G =

S_{4}

$S_4$ 24阶

，因为此子组的左，右陪伴重合（类与整个组的补码相同）

S_{4}

$S_4$ ）。然后将表4折叠成较小的4×4表（换向器），该表包含换向器为1的新子组的元素G''= {1,8,17,24}。表4说明了该组的可解性

S_{4}

$S_4$ 。

结论

本文讨论了组理论的一些主要规定，这些规定经常用于技术性（而非理论和数学）性质的出版物中。对这些出版物的理解程度很大程度上取决于拥有的数学工具。

对于一个组，给出了一个同态映射到商组的例子和技术。

数值示例旨在确保所提供材料的可用性，并通过仔细分析甚至手持铅笔进行重复，在很大程度上帮助其理解和吸收。经典手册中根本没有提供。这通常归因于节省空间和时间。

我正在等待读者的回应，这将使您明确是否继续这种风格。

文学

Nadobin A.A.的Avdoshin S.M.离散数学。模块化代数，密码学，编码。 -M .: DMK出版社，2017.-352羽

阿基莫夫O.E.离散数学，逻辑，组，图形-莫斯科：实验室基础。锌。2001.-352羽

安德森（Anderson D.A.）离散数学和组合数学），莫斯科：威廉姆斯，2003年，第960页。

Berlekamp E.代数编码理论。 -M .:米尔（Mir），1971.-478羽

Vaulin A.E.计算机安全问题中的离散数学。 H 1- SPb。：VKA图片。 A.F.莫扎伊斯基，2015.219羽

Vaulin A.E.计算机安全问题中的离散数学。 H 2- SPb。：VKA即时。 A.F.莫扎伊斯基，2017.-151羽

D. Gorenstein，有限简单组。 -M .：米尔，1985.-352页。

Graham R.，Knut D.，Ptashnik O.具体数学。信息学基础.-M .: Mir，1998.-703页。

Elizarov V.P.端环。 -M.：Helios ARV，2006年。 -304羽

伊万诺夫（Ivanov B.N.）离散数学：算法和程序-M .: Lab。Base。知识。，2001.280羽

Yerusalimsky Y. M.离散数学：理论，问题，应用-M。：Vuzovskaya kniga，2000.280羽。

Lidl R.，Niederreiter G.有限场：2卷。第1卷-M .: Mir，1988。 -430羽

Lidl R.，Niederreiter G.有限场：2卷。第2卷-M .: Mir，1988。 -392羽

Lyapin E.S.，Aizenshtat A.Ya.，Lesokhin M.M.，关于群体理论的练习。-莫斯科：瑙卡，1967.-264

咕utter声抗干扰信息传输的基础。 -L Energoatomizdat，1990，288羽

纳贝宾（A.A. Nabebin），离散数学，莫斯科：实验室。知识。，2001.280羽

诺维科夫程序员的离散数学。-SPb。：Peter，2000.-304 p。

Hall M. Group Theory.-M。：伊兹德。伊利诺伊州，1962.-468羽

Shikhanovich Yu.A. 组，环，格子。-SPb。：Kirtsideli，2006年。-368羽

Shneperman L.B. 问题和练习中的代数和数论课程：2小时内第2部分。-Mn。：Vysh。shk。，1987.-256羽

Shneperman L.B. 代数和数论中问题的集合-明斯克：Design PRO，2000年-240页。

编码和加密的数学基础

导览出版物

团体

对称组 小号4S_4

组态射

换向器

结论

文学

More articles:

对称组 $S_4$