在本文中,我们将使用Wolfram Mathematica查看具有新属性的窗口函数的输出。还假定读者在所讨论问题的背景下对数字信号处理有一般的了解,并且至少熟悉Wikipedia的文章。
介绍
从历史上看,第一个窗口函数出现在试图通过减小旁瓣幅度来改善其频谱特性的过程中-因为当信号乘以窗口函数时,它们的频谱就被卷积了,这为分析带来了一些限制。那时,在20世纪50年代,计算能力不允许轻松自然地操纵符号计算,因此选择最佳参数非常困难。这就是为什么使用不同名称调用功能的原因之一-相当长的一段时间以来,不同的研究人员已经研究了它们,或者更确切地说,是它们的光谱特性。这样做的副作用是,现有的一组命名窗口函数被视为一种“标准集”,在此之上什么也找不到。同时,这些窗口的名称不包含有关属性的任何信息,并建议对其分别进行研究和记忆。
分类
所有窗口函数都是通过将某个函数乘以一个矩形函数而获得的,这可以确保确保其时间约束。因此,首先,可以根据其使用的功能对其进行分类:
- 余弦的总和。由于它们的频谱易于计算并且是加权的Sinc函数之和,因此是最广泛的类别。这包括汉恩,汉明,布莱克曼,哈里斯...
- 分段连续多项式。它们是通过简单函数(例如,矩形和三角形)的卷积而获得的。同时,它们的光谱成倍增加,并且发现也不是特别困难。这些包括Dirichlet,Triangular,Parzen,Welch ...
- 所有其他函数-使用指数函数,高斯函数,sinc函数和其他函数,对特定函数的选择本质上是意识形态的,而不是频谱特性。
它们也可以按边缘的属性进行划分:
- 边缘无间隙-值等于零。休息时间是Dirichlet,Hamming和Blackman-Harris。不用-三角,汉恩,坚果
- 没有一阶和其他导数的不连续性
另外两个窗口功能分别突出:
- 凯撒(Kaiser),可让您设置主花瓣的宽度;
- 多尔夫·切比雪夫(Dolph-Chebyshev),其所有旁瓣均等于给定幅度。
它们两个在值和导数的边缘都具有不连续性,并且它们的计算涉及一些困难-Kaiser函数是通过特殊函数(Bessel)计算的,而Dolph-Chebyshev函数是在频域中确定的,并且是通过离散傅里叶逆变换计算的。寻找它们的分析抗衍生物也特别困难。
您可以使用以下简单代码检查窗口函数是否中断:
↓

wins = {DirichletWindow, HammingWindow, BlackmanWindow,
BartlettHannWindow, BartlettWindow, BlackmanHarrisWindow,
BlackmanNuttallWindow, BohmanWindow, ExactBlackmanWindow,
FlatTopWindow, KaiserBesselWindow, LanczosWindow, NuttallWindow};
Table[{f,
Table[Limit[D[f[x], {x, k}], x -> 1/2,
Direction -> "FromBelow"], {k, 0, 4}]}, {f, wins}]</code>
↓
<img src="https://habrastorage.org/webt/rm/wq/8f/rmwq8fjkjxjcox-czh8zevkbd0m.png" />
<code>Plot[Evaluate[Through[wins[x]]], {x, -1, 1}, PlotRange -> {-0.25, 1},
GridLines -> {{-0.5, -0.25, 0.25, 0.5, 1}}, AspectRatio -> 5/8,
PlotLegends -> "Expressions"]↓

逆向工程
让我们看一下Blackman和Nuttel函数的定义:
BlackmanWindow[x] // FunctionExpand↓
NuttallWindow[x] // FunctionExpand↓
它们是频率为偶数(从零开始)和一些系数的3和4余弦波的总和。这些系数从何而来?手动选择它们的可能性不大,至少每个都是单独选择的-毕竟,无论其光谱特性如何,窗口都必须遵守边界条件-至少等于中心的统一性。
让我们尝试自己“发明” Blackman函数。为此,我们定义一个系数未知的函数
f = Function[x, a + b Cos[2 Pi x] + c Cos[4 Pi x]];并组成一个定义边界条件的方程组-中心等于一,边缘等于零,边缘的导数等于零:
ss = Solve[{
f[0] == 1,
f[1/2] == 0,
f'[1/2] == 0
}, {a, b, c}]↓

找到了解决方案,但不是一个,而是很多-取决于Wolfram有礼貌地警告我们的系数a。现在,从找到的解中,我们根据未知系数定义一个新函数: ↓ 很容易看出,对于a = 0.42,我们获得了布莱克曼函数。但是为什么恰好是0.42? 为了回答这个问题,我们需要绘制其频谱图。解析傅立叶变换不是最简单的任务,但是Wolfram也可以处理它,从而使我们免于繁琐的工作。
hx = Function[{x, a},
Piecewise[{{f[x] /. ss[[1]], -1/2 < x < 1/2}}, 0] // Evaluate]

hw = Function[{w, a},
FourierTransform[hx[x, a], x, w] // #/Limit[#, w -> 0] & //
Simplify // Evaluate]↓

注意
, FourierTransform , — , , — . w. — w, , .

以这种形式,函数的图仍然不是很丰富,因为在对数刻度上分析频谱更方便。通过将适当的换算添加到分贝,我们得到了窗口函数频谱的相同常规图形:
代码
Manipulate[
Plot[{
hw[w, a],
hw[w, 0.42]
} // Abs // 20 Log[10, #] & // Evaluate
, {w, -111, 111}, PlotRange -> {-120, 0}, GridLines -> Automatic,
PlotStyle -> {Default, Thin}, PlotPoints -> 50]
, {{a, 0.409}, 0.3, 0.5}]
↓
在更改参数的过程中,我们将观察到类似的结果:

取决于参数a,旁瓣的水平会发生变化,并且在a = 0.42时,它的大小最小且均匀。当a = 0.409时,如果“更好”是指旁瓣的最小可能水平,则我们可以获得更好的结果。
注意
, , .
发展历程
显然,这种微优化根本不值得付出努力。是否可以在不更改初始数据的情况下定性改善此窗口的属性?
前面我们看过窗口函数的输出之和,这些窗口的总和为1,可让您恢复原始信号。让我们在窗口中尝试该技术,看看它如何影响光谱。
让我们定义一个构造重叠窗口的辅助函数,考虑参数范围在-1/2到1/2范围内的变化:

查找反导数,将其移至坐标中心并将其缩放为一个:

↓

在图形上显示:

如您所见,Wolfram在这里也是自己完成的,我们不必手动设置反导数的分段连续定义。现在,我们窗口的视图不仅取决于变量a,而且取决于重叠的程度-随着重叠程度的增加,它将趋于导数的形式:
代码
↓
Manipulate[
Plot[
OverlapShape[hsx, x, a, t]
, {x, -1, 1}, PlotRange -> All, GridLines -> Automatic]
, {{a, 0.404}, 0.4, 0.5}, {{t, 4}, 3, 11}]↓

最后要做的是找到频谱的解析函数,以确定参数a的最佳值。
在这里,如果我们像上次一样尝试直接计算转换,我们将带动Wolfram深入思考。有几种方法可以加快此过程:
-使用离散变换而不是分析变换-最简单的变换。但是真正的数学家不会将数值方法应用于可以找到纯粹解析解的数值方法,而且我们还不会(到目前为止);此外,它还有明显的局限性(在分辨率和频谱限制方面);
-将特定值作为重叠参数传递,并查看结果,尝试查看模式并将其概括化。可行的选择,但需要额外的精神和创造力。让我们把它留作最后的选择。
-直接在频域中进行计算。由于傅立叶变换的以下特性,这是可能的:
1)它是线性的,即图像的总和等于图像的总和。
2)时域中的积分等效于频域中的iw除。
3)时间偏移等效于使用复杂正弦波的调制。
(有关Wikipedia或此处的更多信息)。
因此,有了任意窗口函数的频谱hw,我们可以从中获得一个函数的频谱hwo,该函数的频谱hwo加起来等于一个具有重叠的t:
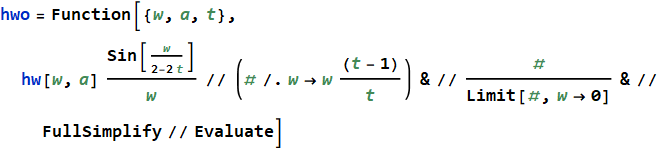
↓
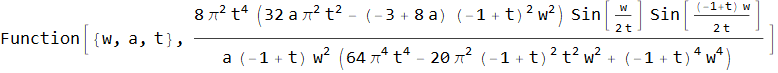
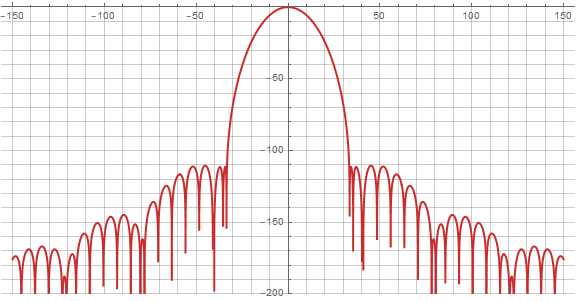
现在我们可以看到频谱的动态变化:

在这里,更改重叠参数将已经以稍微不同的方式影响窗口频谱:

使用了一些参数后,很容易注意到“越多越好”,并且该函数的最佳重叠程度在四个范围内。具体来说,对于t = 4和a= 0.404,我们得到的旁瓣电平不超过-80 dB。这是一个非常好的结果-特别是考虑到传统上用于求和窗口的提高的余弦函数给出了大约-30 dB的波瓣电平。好吧,当明确写出时,我们的新窗口函数将如下所示:
代码
↓
OverlapShape[hsx, x, 404/1000, 4] // PiecewiseExpand // FullSimplify↓
进一步的发展
您还可以采取什么措施进一步降低旁瓣水平?您可以不使用偶数,而可以使用奇数频率的余弦(此处,为紧凑起见,方程组的解直接嵌入函数的定义中):
代码
↓
hx1 = Function[{x, a},
a Cos[1 Pi #] + b Cos[3 Pi #] + c Cos[5 Pi #] & // #[x] /. Solve[{
#[0] == 1,
#[1/2] == 0,
#'[1/2] == 0,
#''[1/2] == 0
}, {a, b, c}][[1]] & // # UnitBox[x] & // Evaluate]↓
在与参数a = 0.6628和重叠水平4.5积分后,获得-90 dB的衰减:

明确地:
您可以再增加一个余弦并增加零导数的数量:
代码
↓
hx2 = Function[{x, a},
a Cos[1 Pi #] + b Cos[3 Pi #] + c Cos[5 Pi #] +
d Cos[7 Pi #] & // #[x] /. Solve[{
#[0] == 1,
#[1/2] == 0,
#'[1/2] == 0,
#''[1/2] == 0,
#'''[1/2] == 0,
#''''[1/2] == 0
}, {b, c, d}][[1]] & // # UnitBox[x] & // Evaluate]↓
在与参数a = 0.5862和重叠水平6.4积分之后,获得-110 dB的抑制:

明确地:
通过对傅立叶变换进行平方运算,从而可以将旁瓣的电平降低得更大得多,从而可以将旁瓣的电平一次减小2倍。这使您摆脱了手动选择参数数量的增加,但是增加了在时域中计算卷积的复杂性。
代码
↓
hx3 = Function[{x, a},
Convolve[hx1[x, a], hx1[x, a], x, y] /. y -> 2 x
// FullSimplify // Evaluate]↓

并且在这里已经可以实现超过160 dB的抑制:

由于公式的大小令人印象深刻,因此我们不会明确给出公式。
超几何窗函数
为了确保函数边界处所需的零个数,我们使用了一个方程组的解法进行搜索,并进行后续积分。这不是很方便-您每次都必须更改方程式的数量。也许有一个更简单,更漂亮的解决方案?有!超几何函数将帮助我们实现这一目标。
简要介绍超几何函数
, . — , . — .
我们的解决方案将如下所示:
哪里
它由两部分之和组成:函数的反导数 将幅度归一化为点(1,1)和具有自由参数的函数,并乘以 为了保留所需数量的零导数:

调整的精度及其对旁瓣分布的影响将取决于我们选择校正形状的功能-有可能的选项需要单独研究。在这种情况下,该功能提供了一个完全可以接受的选项-由于有两个参数,您可以进行更精确的设置。
该公式本身很有趣(方便),因为偶数n简化为多项式,奇数n简化为反正弦和平方根的多项式之和-这使最终公式更紧凑且更易于计算。
通过离散傅里叶变换在这里选择参数已经很容易(而且更快)。我们还需要对重叠函数进行附加定义才能使用三个参数:




例如,从图片中替换参数后,我们的函数将简化为
代码

↓

↓
逆凯撒窗
如果将窗口加总成一个任务不值得,那么最佳窗口就是Kaiser窗口,它可以让您平滑地调整主瓣的宽度。但是,它有一个缺点-由于它是根据贝塞尔函数表示的,因此在数学包之外很难读取它。当然,您可以单独实现Bessel函数-或可以通过基本函数寻找近似值。突然发现,使用凯撒(Kaiser)窗口的光谱功能(时间有限),您可以获得更好的结果-
注意
, .
做出如此明智的决定的代价是不可能纯粹通过分析来表达其频谱-但这并不重要,因为在实践中,无论如何,我们都使用离散傅立叶变换来离散地操作和分析数据。在图的下方,您可以比较它们的光谱,其中红色是原始Kaiser窗口,绿色是其近似值:
代码

↓

↓

在主瓣宽度相同的情况下,旁瓣的水平略低。为了便于使用,您可以用参数k的近似值绘制一张表以获得所需的旁瓣抑制水平:
寻找逆Kaiser窗口的反导数的近似值仍然是一个单独的有趣问题。到目前为止,只能通过幂级数来表达它,而幂级数的收敛速度很慢:
也许数学专家可以在评论中提出更好的解决方案。
结论
尽管数字信号处理是一门完整形成的学科,但仍有发展空间和一些新事物-至少在现有的特殊科学文献中,没有考虑将窗口函数汇总为一个单元的问题;以及现代计算机代数系统的功能,可以从质的角度重新思考积累的知识。
包含所有计算的原始Wolfram Mathematica文档可在GitHub上获得。