数学上的音乐是什么?什么是“ la”或“ mi”?在吉他上,声音的确切形成方式已广为人知。
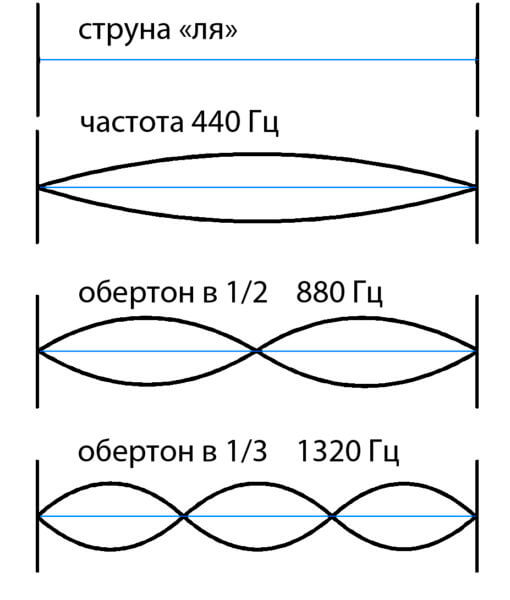
声音为“ mi”(第一弦的自由声音),声音为“ la”(第一弦夹在第五个弦上)。 “ La”为440 Hz。 440 Hz是什么意思?那是弦每秒振动的440倍。 “ mi”声音比“ la”声音(钳制在第5个品格)低5个半音。

再降低7个半音,我将再次得到“ mi”,即八度。为什么第一根弦的自由发声和夹在第12品格上的弦的发声都被称为相同的单词“ mi”?

在我们看来,相同的音符正在演奏。事实是,到此为止的弦的长度(第12品格上的``mi'')被精确地分成两半:
这意味着,根据物理定律,弦的其余部分的振动将是整个弦的振动的两倍。
每次我退弦并将其夹在下一个琴格(指板上垂直线所表示的部分)上时,正如音乐家所说,声音会升高一个半音。
请注意,指板上的琴格宽度不同。它们逐渐逐渐变细,因为为了将频率提高一个半音,您必须将字符串的长度减少一定的次数。
通过关注“在...上的东西”被转换为“在...中的东西”这一事实,我在暗示什么?数学家会说,(在某些条件下)只有一个函数,其中+变为x(乘)。这个函数称为对数。
这意味着我们的耳朵在缩短弦线并提高声音一定次数后,会感觉到它在提高一个半音。也就是说,每个品格将琴弦缩短相同的次数,并且我们的耳朵说我们上升了一个半音,到达音符“ E”并得到一个八度。我们的听觉器官是对数的。
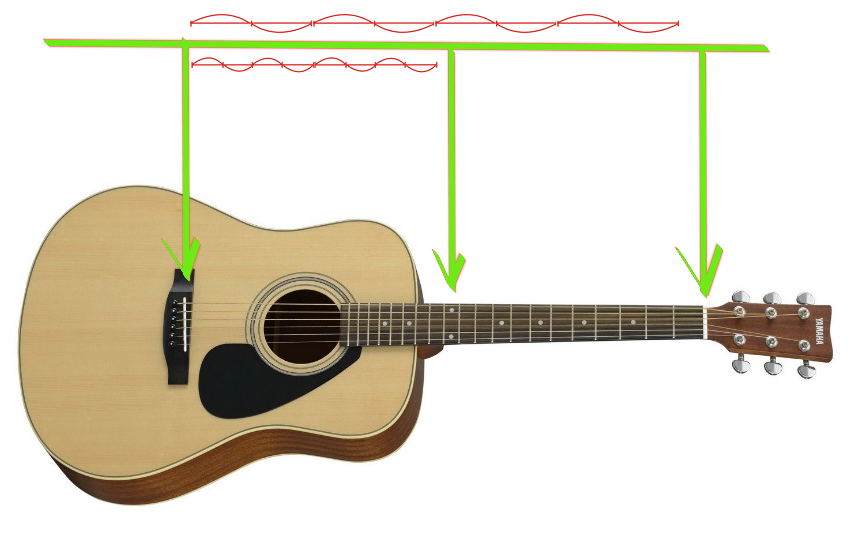
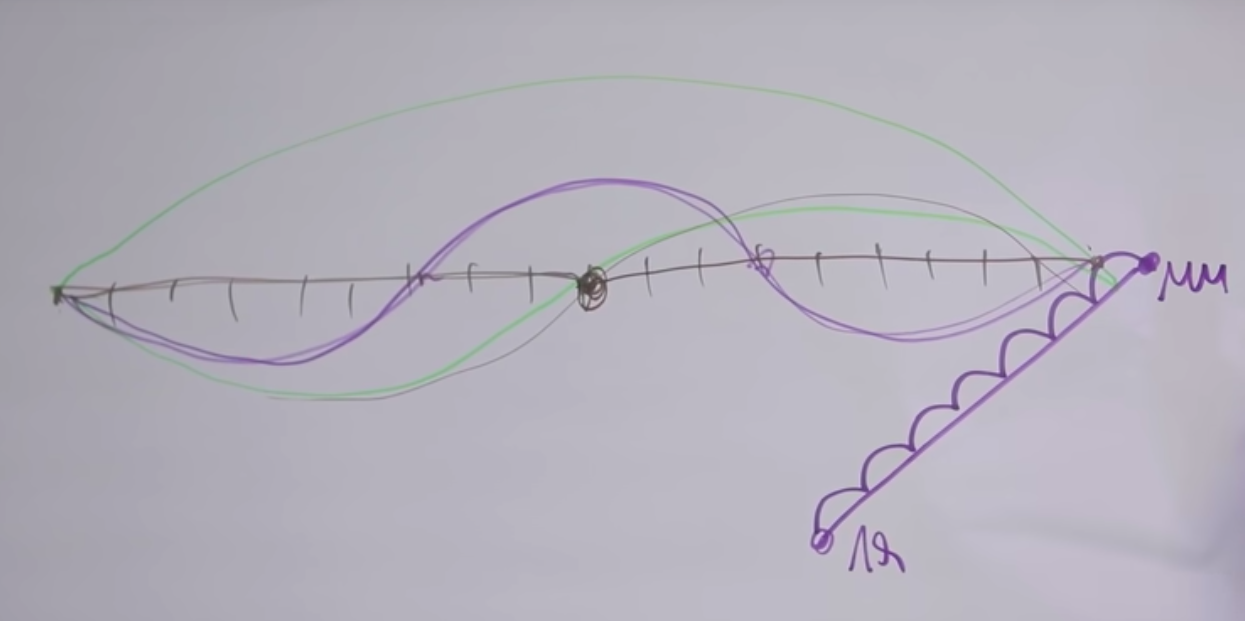
我们说“ mi”和“ mi”相差两次,这在声音上是显而易见的。上弧是全开的。当我们将其夹在中间时,弦开始振动,如中间的图中所示。
为什么声音相似?事实上,随着琴弦的主振动,实际上,在所有频率下,同一琴弦的振动都会发生,其中振动部分的长度与频率成反比。
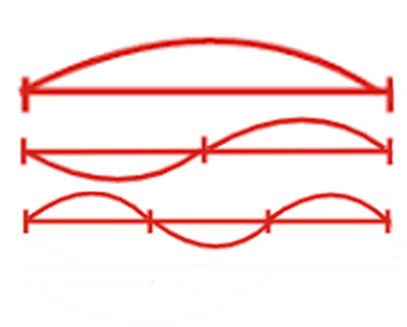
因此,如果将长度减小整数倍,则可以听到相应的泛音。相应的泛音由给定的字符串实现。如果给定的琴弦部分固定在这两个点处振动(下图),则其音调将高出三倍。
相同频率的声音被耳朵感知到。我们划分了几次的所有泛音,即半段的任何划分既是自动划分又是大段。而且只有大部分的某些划分不适合半划分方案。
如果我们将偶数编号的较高音调用于长字符串,则它们将是一半缩短的字符串的较高音调。绝对不会出现任何短弦的缩短声音。因此,我们觉得我们听到的所有声音在这些时候都是重合的,我们将其视为一个音符。
更有意思的是,有些音符会经过几个半音,并且在我们的耳朵中被感知为谐音,和弦,令人愉悦的声音,而不是割伤我们的耳朵。这些笔记是什么?
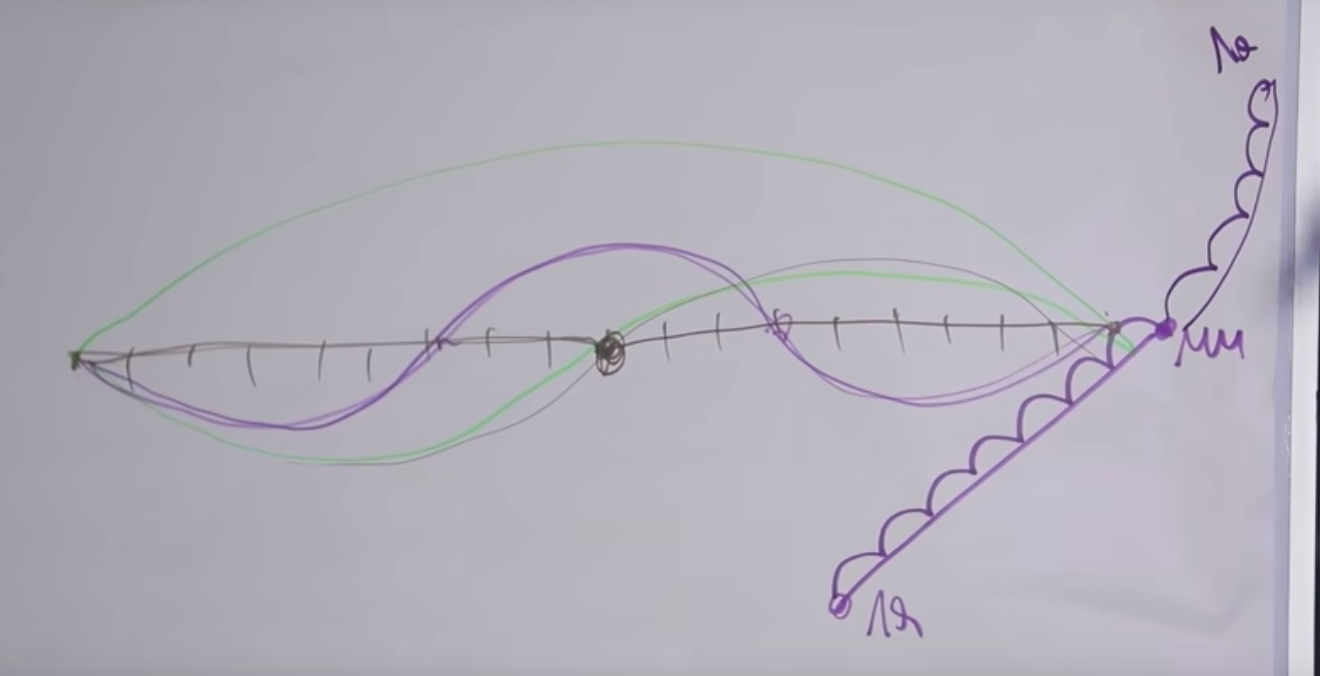
如果您采用7个半音,请记下音符“ A”并将声音提高7个半音,直到下一个“ E”,这两个音符将听起来不错。
如果您再退后5个半音,则下一个八度音阶将有较高的“ la”。由于某些原因,这个间隔对我们来说听起来也很愉快。让我们把它弄清楚。
首先,如果每增加1个半音就增加了振荡频率一定次数,则将其指定为x。如果需要再加一个半音,则已经有x * x,即x 2。如果我将其提高了12个半音(x 12),那么它应该精确地提高了2倍。我们得到方程x 12 = 2。
因此,增加1个半音意味着在x = 12时字符串收缩√2,或者,其是相同的,通过提高声音的频率12 √2。
与“ la”和“ mi”有什么关系呢?为什么7个半音听起来很旋律?让我们提高程度:
多么令人愉快,这个数目很好?
在上古的某个时候,发明了调音的键盘,精确地录制了音乐。您可以在吉他上很好地看到它,也可以在钢琴上找到它,它藏在里面,如果您看进去,就可以看到琴弦。
现在,这个数字非常接近3/2。如果使用计算器进行计算,它将非常准确。这意味着“ mi”大约是前一个“ la”的1.5倍。那些。提升7个音调等同于上升3/2次,这意味着我们有很多相同的上部泛音。
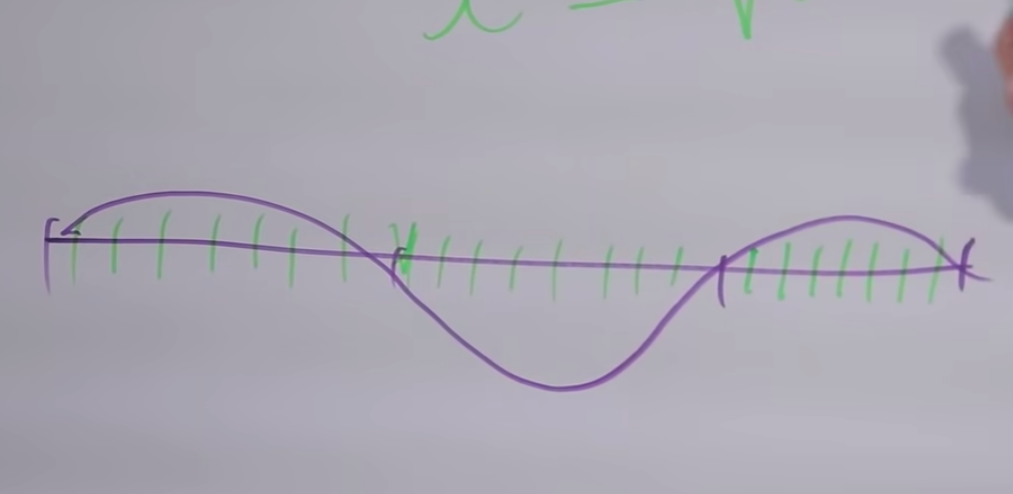
因为任何小段整数的除法都将是整个段的整数除法。相应地,将原始切割除以碎片数(三的倍数)将是小片段(⅓)的划分,也是⅔的划分。当我们从长度上离开⅔时将频率提高到3/2,我们增加了大约7个半音,我们将有许多常见的泛音,这将是令人愉快的谐音。
剩下的4/3正好是剩下的5个半音,即3/2 x 4/3 = 2,仅一个八度。对应于公式x71243。该值非常接近4/3,但不是100%。该数字是非理性的,不能写为小数,不能写为整数除以整数。
我听说有在印度的仪器(西塔琴),其中八度分为19个部分,即它们的半音= 1/19八度,19x2。

而且,x121932的准确性已经很高,这意味着,如果您在这样的印度乐器上从19个乐段中退后12个,那么在这种共鸣中,将会有更多的重合泛音,并且这个间隔听起来像是润唇膏。
关于音乐和数学,有很多有趣的事情要说。特别是,如果您在任何初始音符中添加4个半音,然后再添加3个半音,即会感知到大和弦。 0-4-3。未成年人,如果您在开头添加3,然后再添加4,即0-3-4。和弦的三个音符的第一个和最后一个将是“相同的”,仅相差7个半音,但是中音将创建我们对和声的感知,并以次要或主要模式进行调音。
似乎音乐和数学有什么共同点?而且有很多共同点,数学家和音乐家经常交流,而且,数学家容易理解音乐家,可以说,他们掌握了一个半音。
几个有用的链接: