
我是谁
我叫德米特里·伊万诺夫(Dmitry Ivanov)。我是圣彼得堡HSE经济学的二年级研究生。我在JetBrains Research的“代理系统和强化学习”研究小组中工作,在经济高等学校的博弈论与决策国际实验室中工作。除了PU学习之外,我还对机器学习和经济学交叉领域的强化学习和研究感兴趣。
前言
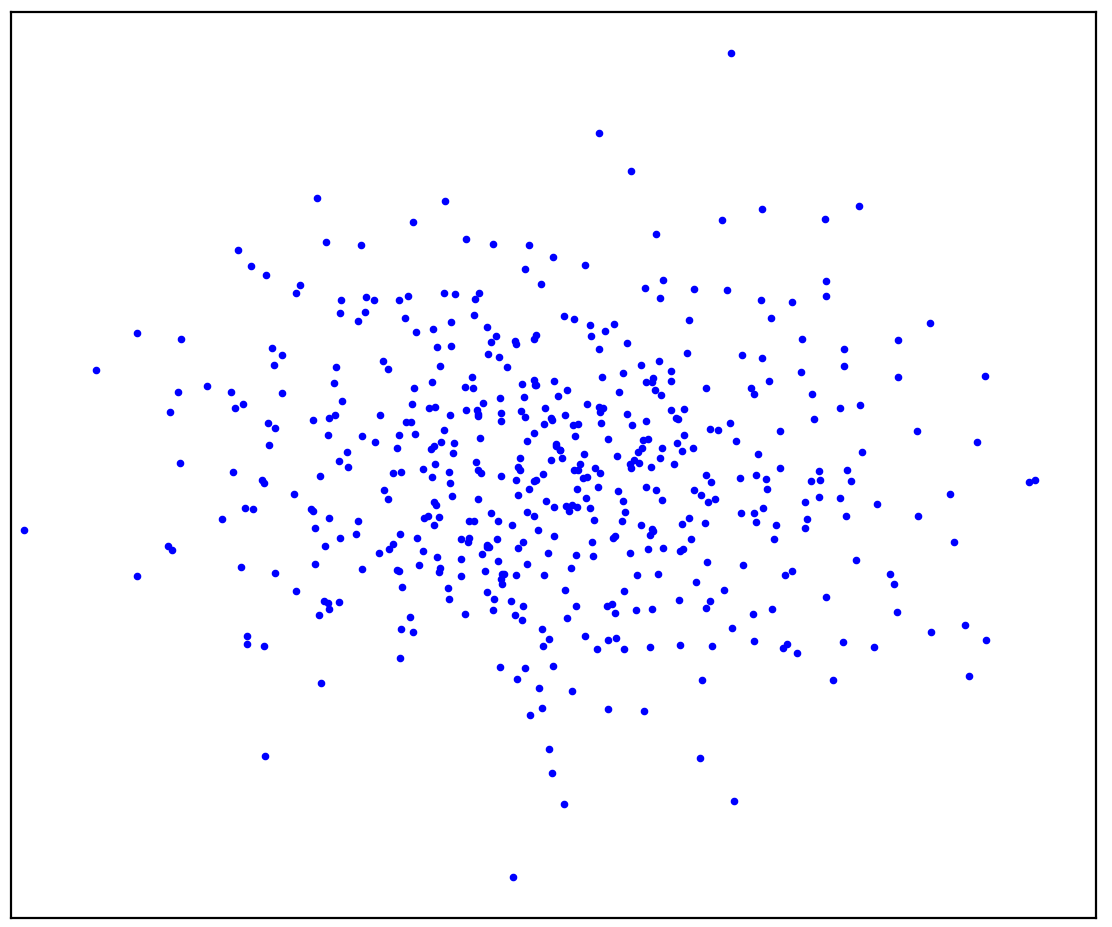
数字:1a。正数据
图1a显示了由某种分布生成的一组点,我们称其为正。不属于正分布的所有其他可能点将称为负。尝试在思维上画一条线,将呈现的积极点与所有可能的消极点分开。顺便说一句,此任务称为“异常检测”。
答案在这里

. 1.

. 1.
您可能想像过图1b:将数据圈成椭圆形。实际上,这就是多少种异常检测方法。
现在让我们稍微改变一下问题:让我们获得更多信息,一条直线应该将正点与负点分开。尝试在您的脑海中画出它。
答案在这里
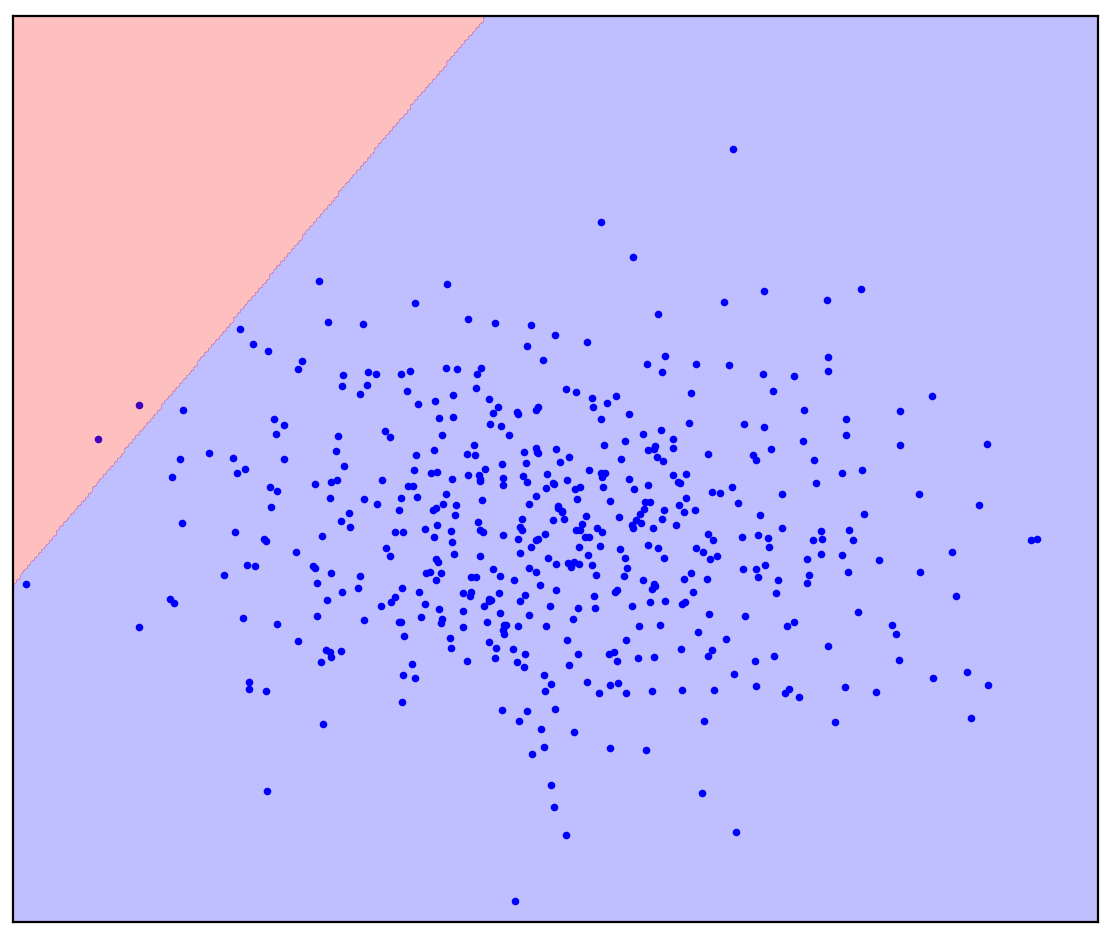
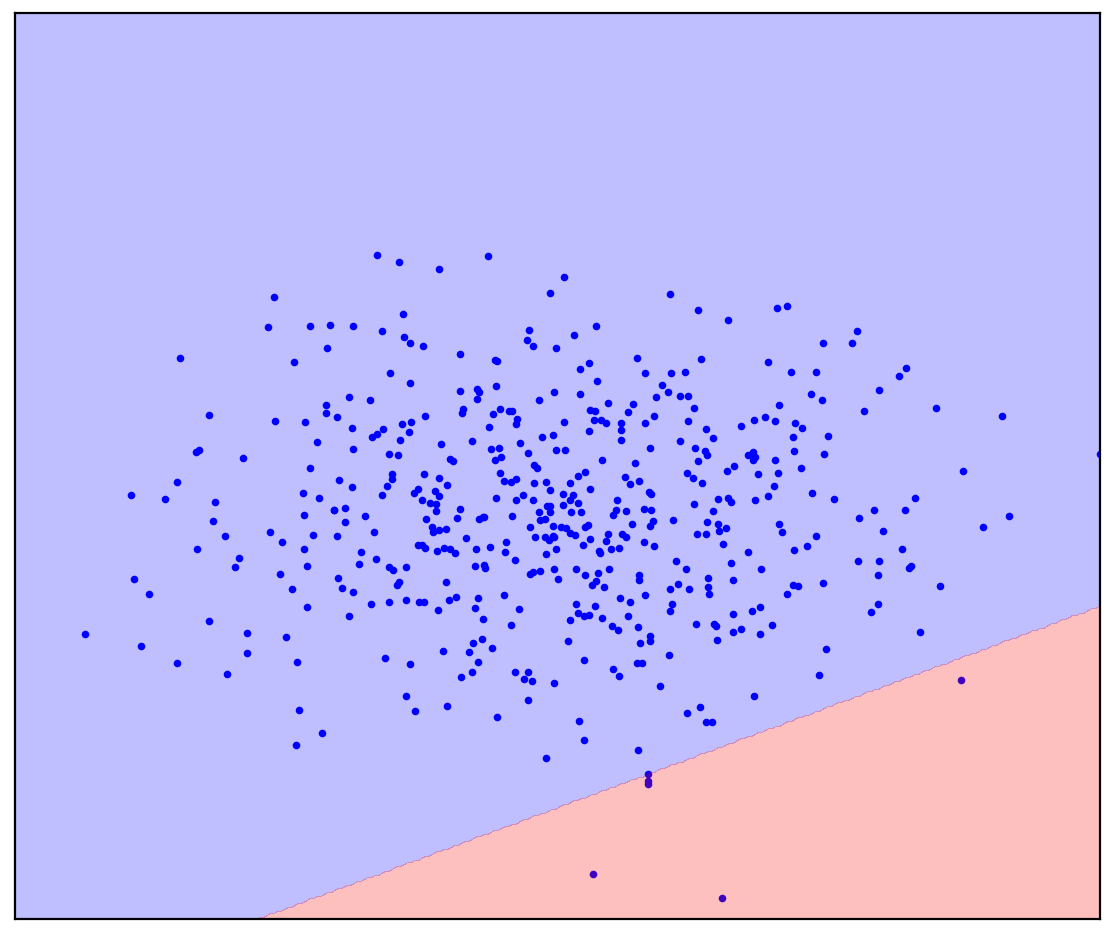
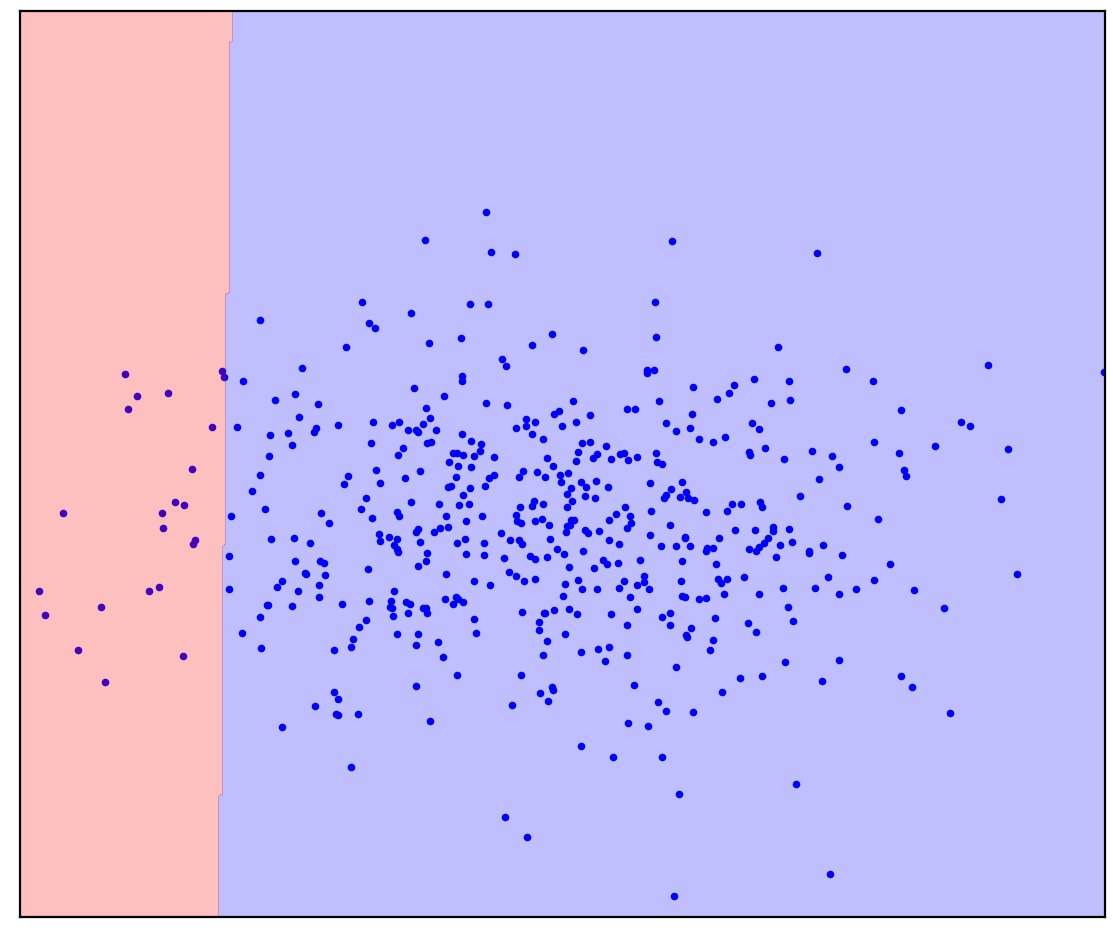
. 1. ( One-Class SVM)



. 1. ( One-Class SVM)
在直线分隔线的情况下,没有单个答案。画一条直线的方向还不清楚。
现在,我将在图1d中添加未分配点,其中包含正负值。最后一次,我将请您尽一切努力,想象一下将正负分界线。但是这一次,您可以使用未标记的数据!

数字:1天 正(蓝色)和未标记(红色)点。未标记的点由正负组成
答案在这里

. 1.

. 1.
变得容易了!尽管我们事先不知道每个特定的未标记点是如何生成的,但可以通过将它们与正值进行比较来粗略地标记它们。看起来像蓝色的红点可能是阳性的。相反,不同的可能是负面的。结果,尽管事实是我们没有“纯”阴性数据,但有关它们的信息可以从未标记的混合物中获得,并用于更准确的分类。这就是我要谈论的正无标签学习算法的作用。
介绍
阳性无标签(PU)学习可以转换为“从阳性和无标签数据中学习”。实际上,对于只有一个类别的带标签数据但两个类别的数据都没有标签混合的情况,PU学习类似于二进制分类。在一般情况下,我们甚至不知道混合物中有多少数据对应于一个阳性类别,而有多少数据对应于一个阴性类别。基于此类数据集,我们想要构建一个二进制分类器:与两个类的纯数据存在时相同。
作为玩具示例,请考虑对猫和狗的图片进行分类。我们有一些猫的图片,还有更多猫和狗的图片。在输出中,我们想要一个分类器:一个为每张图片预测猫被描绘的概率的函数。同时,分类器可以标记我们现有的猫狗混合图像。同时,手动标记图片来训练分类器可能很困难/昂贵/费时/不可能,您想要没有它就做。
PU学习是很自然的任务。现实世界中发现的数据通常很脏。从脏数据中学习的能力似乎是相对高质量的有用的生活技巧。尽管如此,我遇到的矛盾的是,很少有人听说过PU学习,甚至很少人知道任何特定方法。所以我决定谈论这个领域。

数字:2.JürgenSchmidhuber和Yann LeCun,NeurIPS 2020
PU学习的应用
我将非正式地将对PU学习有用的情况分为三类。
第一类可能是最明显的:可以使用PU学习代替通常的二进制分类。在某些任务中,数据本来就有点脏。原则上,可以忽略这种污染,可以使用常规分类器。但是,训练分类器(Kiryo等人,2017)或训练后的预测本身(Elkan&Noto,2008)时,损失函数的变化可能很小,分类变得更加准确。
例如,考虑鉴定负责疾病基因发展的新基因。标准方法是将已经发现的疾病基因视为阳性,将所有其他基因视为阴性。显然,该阴性数据中可能存在尚未发现的疾病基因。此外,任务本身就是在“阴性”数据中搜索此类疾病基因。这种内部矛盾在这里被注意到:(Yang等,2012)。研究人员偏离了常规方法,将与已经发现的疾病基因无关的基因视为未标记的混合物,然后应用了PU学习方法。
另一个例子是从专家示范中学习强化。面临的挑战是训练代理以与专家相同的方式行事。这可以使用生成的对抗模仿学习(GAIL)方法来实现。 GAIL使用GAN式(生成对抗网络)架构:代理生成轨迹,以便区分器(分类器)无法将其与专家的演示区分开。 DeepMind的研究人员最近注意到,在GAIL中,鉴别器解决了PU学习问题(Xu和Denil,2019年)...通常,鉴别器认为专家数据为正,而生成的数据为负。当生成器无法生成看起来像是正数的数据时,这种近似在训练开始时就足够准确。但是,随着训练的进行,生成的数据看起来更像专家数据,直到在训练结束时区分者变得无法区分为止。因此,研究人员(Xu&Denil,2019)认为生成的数据是混合比例可变的未标记数据。后来,在生成图像时以类似的方式修改了GAN (Guo等人,2020年)。

数字: 3. PU学习作为标准PN分类的类似物
在第二类中, PU学习可以作为一类分类(OCC)的类似物用于异常检测。我们已经在序言中看到了未加标签的数据将如何提供帮助。所有OSS方法无一例外都必须对负数据的分布进行假设。例如,明智的做法是将正数据圈入一个椭圆(在多维情况下为超球体),在椭圆之外所有点均为负。在这种情况下,我们假设负面数据是均匀分布的(Blanchard等,2010)。... PU学习方法无需做出这样的假设,而是可以基于未标记的数据来估计负面数据的分布。如果两个类别的分布强烈重叠,这一点尤其重要(Scott&Blanchard,2009)。使用PU学习进行异常检测的一个例子是假评论检测(Ren等人,2014)。

数字:4.虚假评论的例子
在俄罗斯公共采购拍卖中发现腐败
PU学习的第三类可以归因于不能使用二进制或单类分类的问题。例如,我将向您介绍我们的项目,以检测俄罗斯公共采购拍卖中的腐败行为(Ivanov&Nesterov,2019)。
根据法律规定,所有要花费一个月的时间进行解析的人都可以将所有公共采购拍卖的完整数据放置在公共领域。我们收集了2014年至2018年超过100万次拍卖的数据。谁投入,何时何地,谁赢得,在什么时期举行拍卖,谁举行,购买了什么-所有这些都在数据中。但是,当然,没有标签“腐败在这里”,因此您无法构建普通的分类器。相反,我们应用了PU学习。基本假设:具有不公平优势的参与者将永远获胜。使用此假设,拍卖中的失败者可被视为公平(积极),而胜利者则可被视为不诚实(未标记)。通过这种方式进行设置时,PU学习方法可以根据赢家和输家之间的细微差异找到数据中的可疑模式。当然,在实践中会遇到困难:需要对分类器的特征进行准确的设计,对其预测的可解释性进行分析,并对有关数据的假设进行统计验证。
根据我们非常保守的估计,数据中大约9%的拍卖是腐败的,因此该国每年损失约1.2亿卢布。损失似乎并不大,但我们研究的拍卖仅占公共采购市场的1%。


数字:5.俄罗斯不同地区腐败的公共采购拍卖所占的份额(Ivanov&Nesterov,2019年)
结束语
为了不给人留下PU是解决人类所有麻烦的印象,我将提一下陷阱。在常规分类中,我们拥有的数据越多,分类器就越准确。此外,将数据量增加到无穷大,我们可以接近理想的分类器(根据贝叶斯公式)。因此,PU学习的主要收获在于它是一个不适定的问题,即即使数据量无限也无法明确解决的问题。如果知道这两种类别在未标记数据中的比例,情况会更好,但确定该比例也是一个不适定的问题(Jain等人,2016)... 我们可以定义的最好是比例的间距。此外,PU学习方法通常不提供估算此比例并认为已知的方法。有单独的方法对其进行估计(此任务称为“混合比例估计”),但它们通常很慢和/或不稳定,尤其是当两种类别在混合物中的表示非常不均匀时。
在本文中,我讨论了PU学习的直观定义和应用。另外,我可以通过公式和解释来介绍PU学习的形式定义,以及经典和现代的PU学习方法。如果这篇文章引起人们的兴趣,我会写续集。
参考书目
Blanchard, G., Lee, G., & Scott, C. (2010). Semi-supervised novelty detection. Journal of Machine Learning Research, 11(Nov), 2973–3009.
Elkan, C., & Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining — KDD 08, 213. https://doi.org/10.1145/1401890.1401920
Guo, T., Xu, C., Huang, J., Wang, Y., Shi, B., Xu, C., & Tao, D. (2020). On Positive-Unlabeled Classification in GAN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8385–8393.
Ivanov, D. I., & Nesterov, A. S. (2019). Identifying Bid Leakage In Procurement Auctions: Machine Learning Approach. ArXiv Preprint ArXiv:1903.00261.
Jain, S., White, M., Trosset, M. W., & Radivojac, P. (2016). Nonparametric semi-supervised learning of class proportions. ArXiv Preprint ArXiv:1601.01944.
Kiryo, R., Niu, G., du Plessis, M. C., & Sugiyama, M. (2017). Positive-unlabeled learning with non-negative risk estimator. Advances in Neural Information Processing Systems, 1675–1685.
Ren, Y., Ji, D., & Zhang, H. (2014). Positive Unlabeled Learning for Deceptive Reviews Detection. EMNLP, 488–498.
Scott, C., & Blanchard, G. (2009). Novelty detection: Unlabeled data definitely help. Artificial Intelligence and Statistics, 464–471.
Xu, D., & Denil, M. (2019). Positive-Unlabeled Reward Learning. ArXiv:1911.00459 [Cs, Stat]. http://arxiv.org/abs/1911.00459
Yang, P., Li, X.-L., Mei, J.-P., Kwoh, C.-K., & Ng, S.-K. (2012). Positive-unlabeled learning for disease gene identification. Bioinformatics, 28(20), 2640–2647.