
大家好,今天我们将介绍JPEG压缩算法。许多人不知道JPEG并不是一种算法而是一种格式。您看到的大多数JPEG图像都是JFIF(JPEG文件交换格式),在其中应用了JPEG压缩算法。到本文结尾,您将对该算法如何压缩数据以及如何在Python中编写解压缩代码有更好的了解。我们不会考虑JPEG格式的所有细微差别(例如,逐行扫描),而只会在编写自己的解码器时谈论该格式的基本功能。
介绍
如果已经写了数百篇文章,为什么还要在JPEG上写另一篇文章?通常,在此类文章中,作者仅谈论格式是什么。您无需编写拆包和解码代码。即使您编写某些内容,它也将是C / C ++,并且许多人都无法访问此代码。我想打破这一传统,并使用Python 3向您展示基本JPEG解码器的工作原理。它会根据这个代码,由麻省理工学院开发,但我会改变很多关于可读性和清晰度的缘故。您可以在我的存储库中找到本文的修改后的代码。
JPEG的不同部分
让我们从Ange Albertini的照片开始。它列出了简单JPEG文件的所有部分。我们将分析每个部分,当您阅读本文时,您将不止一次返回此插图。
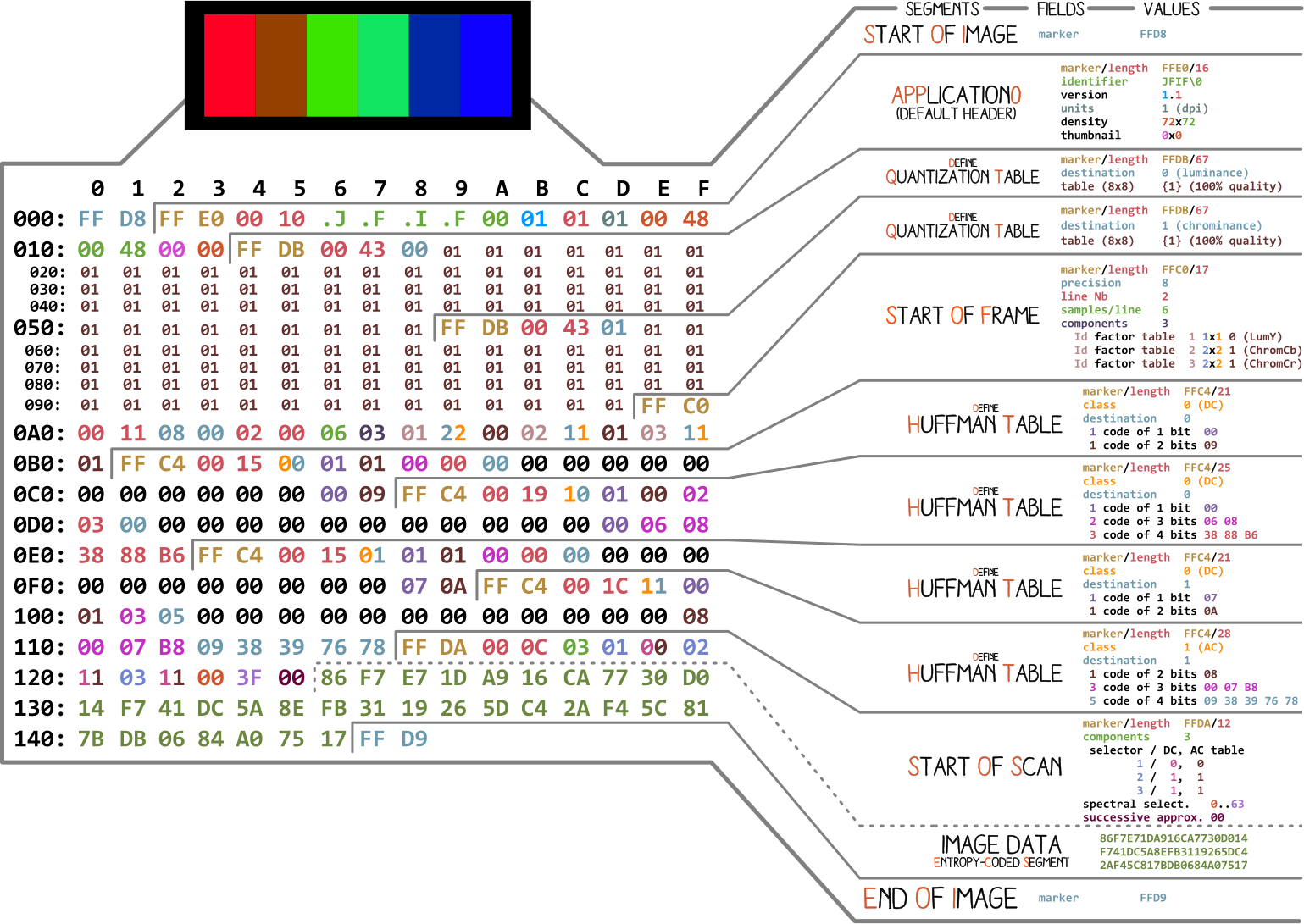
几乎每个二进制文件都包含多个标记(或标头)。您可以将它们视为某种书签。它们对于使用文件至关重要,并且被文件之类的程序使用(在Mac和Linux上),以便我们可以找到文件的详细信息。标记准确指示某些信息在文件中的存储位置。通常,标记是根据
length特定段的长度值()放置的。
文件的开始和结束
对我们重要的第一个标志是
FF D8。它定义了图像的开始。如果找不到,则可以假定标记位于其他文件中。标记同样重要FF D9。它说我们已经到了图像文件的末尾。在每个标记之后,除了FFD0-FFD9和范围外FF01,都会立即出现该标记段长度的值。文件开头和结尾的标记始终为两个字节长。
我们将使用此图像:

让我们编写一些代码来查找开始和结束标记。
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
为了解压缩图像的字节,我们使用了struct。
>H告诉struct它读取数据类型unsigned short并按从高到低的顺序(big-endian)使用它。 JPEG数据以最高到最低的格式存储。只有EXIF数据可以采用低字节序格式(尽管通常不是这种情况)。大小short为2,因此我们unpack从传输了两个字节img_data。我们怎么知道它是short什么?我们知道JPEG中的标记由四个十六进制字符表示:ffd8。一个这样的字符等效于四个位(半字节),因此四个字符将等同于两个字节short。
在“开始扫描”部分之后,将立即扫描扫描的图像数据,没有特定的长度。它们持续到文件标记结束,因此当我们找到“开始扫描”标记时,我们会手动“搜索”它。
现在,让我们处理其余的图像数据。为此,我们首先研究理论,然后继续编程。
JPEG编码
首先,让我们谈谈JPEG中使用的基本概念和编码技术。编码将以相反的顺序进行。根据我的经验,如果没有解码,将很难弄清。
下面的插图对您来说还不清楚,但是在您学习编码和解码过程时,我会给您一些提示。这是JPEG编码的步骤(源):
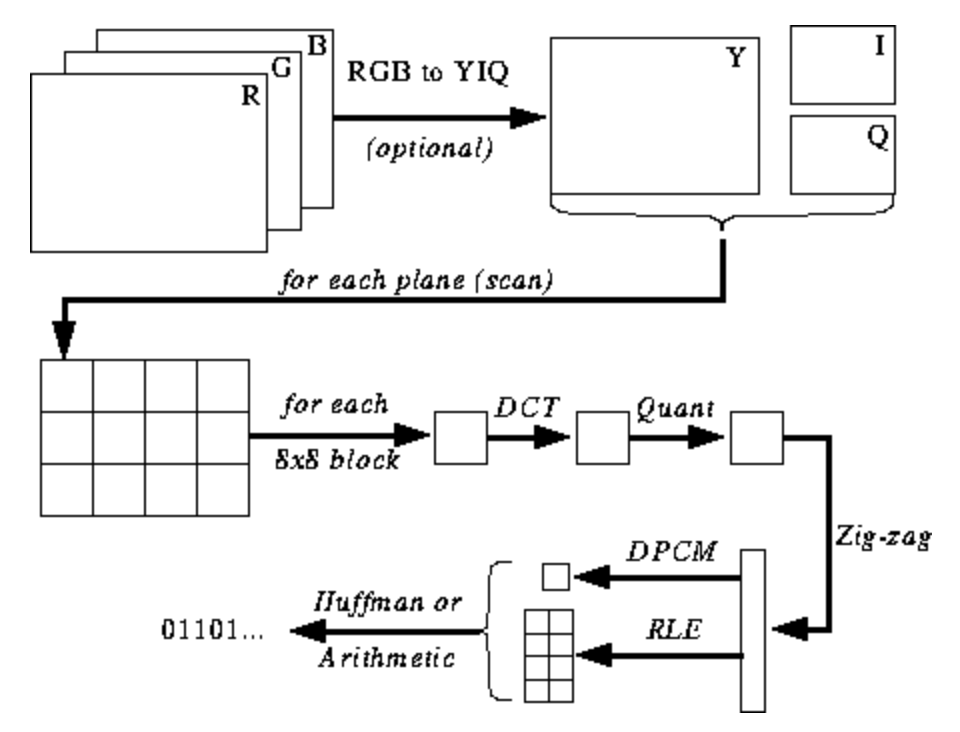
JPEG色彩空间
根据JPEG规范(ISO / IEC 10918-6:2013(E)第6.1节):
- 仅使用一种成分编码的图像被视为灰度数据,其中0为黑色,255为白色。
- 用三个分量编码的图像被认为是在YCbCr空间中编码的RGB数据。如果图像包含第6.5.3节中所述的APP14标记段,则根据APP14标记段中的信息将颜色编码视为RGB或YCbCr。RGB和YCbCr之间的关系是根据ITU-T T.871 | ISO / IEC 10918-5。
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
JPEG算法的大多数实现使用亮度和色度(YUV编码)代替RGB。这是非常有用的,因为人眼在分辨小区域中的高频亮度变化方面很差,因此您可以降低频率,并且人不会注意到这种差异。它有什么作用?高度压缩的图像,几乎看不到质量下降。
与RGB中一样,每个像素都用三个字节的颜色(红色,绿色和蓝色)编码,因此在YUV中使用了三个字节,但是它们的含义不同。 Y分量定义颜色的亮度(亮度或亮度)。 U和V定义颜色(色度):U负责蓝色部分,V-负责红色部分。
这种格式是在电视还不很普遍的时候开发的,工程师们希望将相同的图像编码格式用于彩色和黑白电视广播。在此处阅读有关此内容的更多信息。
离散余弦变换和量化
JPEG将图像转换为8x8像素块(称为MCU,最小编码单位),更改像素值的范围以使中心为0,然后对每个块应用离散余弦变换,并使用量化压缩结果。让我们看看这意味着什么。
离散余弦变换(DCT)是一种将离散数据转换为余弦波组合的方法。乍看之下,将图片转换成一组余弦看起来像是徒劳的练习,但是当您了解下一步时,您将了解原因。 DCT采用8x8像素块,并告诉我们如何使用8x8余弦函数矩阵重现该块。更多细节在这里。
矩阵如下所示:

我们将DCT分别应用于每个像素组件。结果,我们得到了一个8x8的系数矩阵,该矩阵显示了输入8x8矩阵中每个(所有64个)余弦函数的贡献。在DCT系数矩阵中,最大值通常在左上角,而最小值在右下角。左上角是最低频率的余弦函数,右下角是最高的频率。
这意味着在大多数图像中,都有大量的低频信息和一小部分的高频信息。如果为每个DCT矩阵的右下部分分配了0值,那么对于我们来说,所得图像将看起来相同,因为一个人不会很好地区分高频变化。这就是我们下一步的工作。
我找到了关于这个主题的精彩视频。看一下您是否不了解PrEP的含义:
众所周知,JPEG是一种有损压缩算法。但是到目前为止,我们还没有丢失任何东西。我们只有8x8 YUV分量块转换为8x8余弦函数块,而不会丢失信息。数据丢失阶段是量化。
量化是一个过程,当我们从某个范围取两个值并将其转换为离散值时。在我们的情况下,这只是一个狡猾的名字,它将最终DCT矩阵中的最高频率系数降低为0。当使用JPEG保存图像时,大多数图形编辑器会询问您要设置的压缩级别。这是高频信息丢失的地方。您将不再能够从生成的JPEG图像重新创建原始图像。
根据压缩率使用不同的量化矩阵(事实:大多数开发人员都拥有创建量化表的专利)。我们将系数的DCT矩阵除以量化矩阵,将结果四舍五入为整数,得到量化矩阵。
让我们来看一个例子。假设有一个这样的DCT矩阵:

这是通常的量化矩阵:
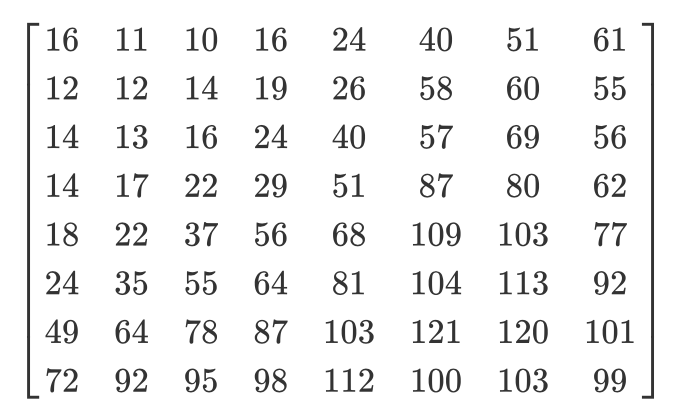
量化矩阵如下所示:

尽管人类看不到高频信息,但是如果您从8x8像素块中删除了太多数据,则图像看起来会太粗糙。在这样的量化矩阵中,第一个值称为DC值,所有其他值称为AC值。如果我们获取所有量化矩阵的DC值并生成新图像,那么我们将获得分辨率比原始图像小8倍的预览图。
我还想指出,由于我们使用了量化,因此我们需要确保颜色落在[0.255]的范围内。如果它们飞出了它,那么您将不得不手动将它们带到该范围。
之字形
量化后,JPEG算法使用锯齿形扫描将矩阵转换为一维形式:
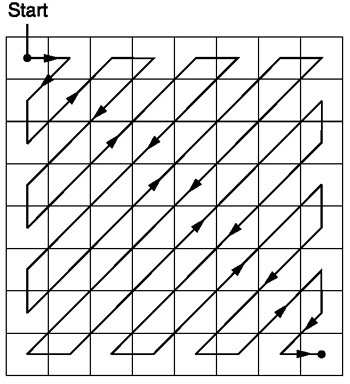
来源。
让我们有一个这样的量化矩阵:
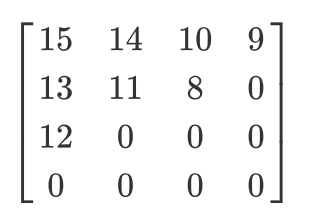
锯齿形扫描的结果如下:
[15 14 13 12 11 10 9 8 0 ... 0]
首选这种编码方式,因为在量化之后,大多数低频(最重要)信息将位于矩阵的开头,而之字形扫描会将这些数据存储在一维矩阵的开头。这对于下一步(压缩)很有用。
行程编码和增量编码
游程长度编码用于压缩重复数据。在锯齿形扫描之后,我们看到在数组末尾大部分为零。长度编码使我们能够利用这个浪费的空间,并使用较少的字节来表示所有这些零。假设我们有以下数据:
10 10 10 10 10 10 10
对序列长度进行编码后,我们得到以下结果:
7 10
我们已经将7个字节压缩为2个字节。
增量编码用于表示相对于其之前的字节的字节。用一个例子来解释会更容易。让我们获得以下数据:
10 11 12 13 10 9
使用增量编码,它们可以表示如下:
10 1 2 3 0 -1
在JPEG中,DCT矩阵的每个DC值都相对于先前的DC值进行了增量编码。这意味着,通过更改图像的第一个DCT系数,您将破坏整个图像。但是,如果更改最后一个DCT矩阵的第一个值,则它将仅影响图像的很小片段。
这种方法很有用,因为图片的第一个DC值往往变化最大,并且使用增量编码时,我们将其余的DC值更接近0,这可以通过霍夫曼编码提高压缩率。
霍夫曼编码
这是一种无损压缩方法。霍夫曼曾经想过:“我可以用来存储自由文本的最小位数是多少?” 结果,创建了编码格式。假设我们有文字:
a b c d e
通常,每个字符占用一个字节的空间:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
这是二进制ASCII编码的原理。如果我们更改映射怎么办?
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
现在,我们需要更少的位来存储相同的文本:
a: 000
b: 001
c: 010
d: 100
e: 011
一切都很好,但是如果我们需要节省更多空间怎么办?例如,像这样:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
霍夫曼编码允许这种可变长度匹配。获取输入数据,最常见的字符与较小的位组合匹配,而频率较低的字符与较大的组合匹配。然后将生成的映射收集到二叉树中。在JPEG中,我们使用霍夫曼编码存储DCT信息。还记得我提到过增量编码DC值使霍夫曼编码更容易吗?我希望你现在明白为什么。经过增量编码后,我们需要匹配更少的“字符”,并且减少了树的大小。
汤姆·斯科特(Tom Scott)播放了一段精彩的视频,解释了霍夫曼算法的工作原理。在继续阅读之前先看一下。
JPEG最多包含四个霍夫曼表,这些表存储在“定义霍夫曼表”中(以开头
0xffc4)。 DCT系数存储在两个不同的霍夫曼表中:一个在Z字形表中的DC值中,在另一个-在Z字形表中的AC值中。这意味着编码时,我们需要将两个矩阵的DC和AC值组合在一起。亮度和色度通道的DCT信息分别存储,因此我们有两组DC和两组AC信息,总共有4个霍夫曼表。
如果图像是灰度的,那么我们只有两个霍夫曼表(一个用于DC,一个用于AC),因为我们不需要颜色。您可能已经发现,两个不同的图像可以具有非常不同的霍夫曼表,因此将它们存储在每个JPEG中非常重要。
现在我们知道了JPEG图像的主要内容。让我们继续进行解码。
JPEG解码
解码可以分为几个阶段:
- 霍夫曼表的提取和位的解码。
- 使用游程长度和增量编码回滚来提取DCT系数。
- 使用DCT系数组合余弦波并为每个8x8块重建像素值。
- 将每个像素的YCbCr转换为RGB。
- 显示生成的RGB图像。
JPEG标准支持四种压缩格式:
- 基础
- 扩展序列
- 进步
- 没有损失
我们将使用基本压缩。它包含一系列紧接着的8x8块。在其他格式中,数据模板略有不同。为了清楚起见,我在图像的十六进制内容的不同部分进行了着色:
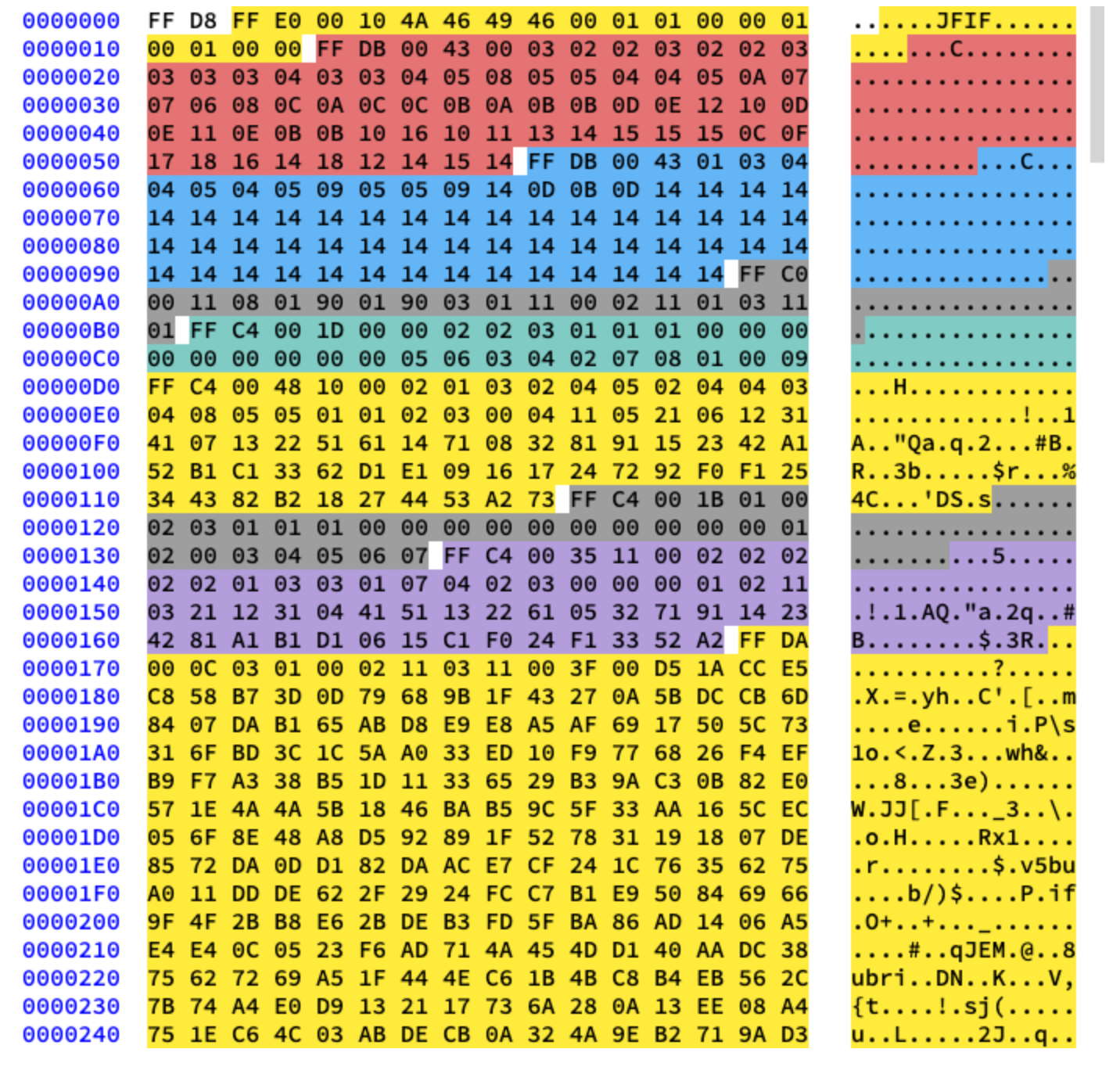
提取霍夫曼表
我们已经知道JPEG包含四个霍夫曼表。这是最后一种编码,因此我们将开始使用它进行解码。该表的每个部分均包含以下信息:
| 领域 | 规模 | 描述 |
|---|---|---|
| 标记ID | 2字节 | 0xff和0xc4标识DHT |
| 长度 | 2字节 | 工作台长度 |
| 霍夫曼表信息 | 1个字节 | 位0 ... 3:表的数量(0 ... 3,否则为错误)位4:表的类型,0 = DC表,1 = AC表位5 ... 7:未使用,必须为0 |
| 性格 | 16字节 | 长度为1 ... 16的代码的字符数,这些字节的总和(n)是必须小于等于256的代码总数 |
| 符号 | n个字节 | 该表包含按增加的代码长度顺序的字符(n =总代码数)。 |
假设我们有一个像这样的霍夫曼表(源):
| 符号 | 霍夫曼码 | 码长 |
|---|---|---|
| 一种 | 00 | 2 |
| b | 010 | 3 |
| C | 011 | 3 |
| d | 100 | 3 |
| Ë | 101 | 3 |
| F | 110 | 3 |
| G | 1110 | 4 |
| H | 11110 | 五 |
| 一世 | 111110 | 6 |
| Ĵ | 1111110 | 7 |
| ķ | 11111110 | 8 |
| 升 | 111111110 | 九 |
它将被存储在这样的JFIF文件中(二进制格式。我使用ASCII只是为了清楚起见):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0表示我们没有长度为1的霍夫曼代码。1表示我们只有一个长度为2的霍夫曼代码,依此类推。在DHT部分中,紧随类和ID之后,数据始终为16个字节长。让我们编写代码以从DHT中提取长度和元素。
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
执行代码后,我们得到以下信息:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
优秀的!我们有长度和元素。现在,您需要创建自己的霍夫曼表类,以便从获得的长度和元素中重建二叉树。我将从这里复制代码:
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBits接受长度和元素,遍历元素,然后将它们放入列表中root。它是一个二叉树,包含嵌套列表。您可以在Internet上阅读霍夫曼树的工作原理以及如何在Python中创建这样的数据结构。对于我们的第一个DHT(从本文开头的图片开始),我们具有以下数据,长度和元素:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
通话后,
GetHuffmanBits列表root将包含以下数据:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTable还包含一种GetCode遍历树并使用霍夫曼表返回解码位的方法。该方法接收比特流作为输入-只是数据的二进制表示形式。例如,的位流abc将为011000010110001001100011。首先,我们将每个字符转换为其ASCII码,然后将其转换为二进制。让我们创建一个类,以帮助将字符串转换为位,然后逐个计数位:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
初始化时,我们给该类二进制数据,然后使用
GetBit和读取它GetBitN。
解码量化表
“定义量化表”部分包含以下数据:
| 领域 | 规模 | 描述 |
|---|---|---|
| 标记ID | 2字节 | 0xff和0xdb标识DQT部分 |
| 长度 | 2字节 | 量化表长度 |
| 量化信息 | 1个字节 | 位0 ... 3:量化表的数量(0 ... 3,否则为错误)位4 ... 7:量化表的精度,0 = 8位,否则为16位 |
| 字节数 | n个字节 | 量化表值,n = 64 *(精度+1) |
根据JPEG标准,默认JPEG图像具有两个量化表:亮度和色度。他们以记号笔开头
0xffdb。我们的代码结果已经包含两个这样的标记。让我们添加解码量化表的功能:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
我们首先定义一个方法
GetArray。这只是从二进制数据中解码可变数目的字节的一种便捷技术。我们还替换了方法中的一些代码decodeHuffman以利用新功能。然后定义了该方法DefineQuantizationTables:该方法读取带有量化表的节的标题,然后使用标头的值作为关键字将量化数据应用于字典。对于亮度,该值可以是0,对于色度,可以是1。JFIF中带有量化表的每个部分都包含64字节的数据(用于8x8量化矩阵)。
如果我们为图片输出量化矩阵,则会得到以下结果:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
解码帧的开始
“帧开始”部分包含以下信息(源):
| 领域 | 规模 | 描述 |
|---|---|---|
| 标记ID | 2字节 | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
在这里,我们对一切都不感兴趣。我们将提取图像的宽度和高度,以及每个分量的量化表数量。宽度和高度将用于从“开始扫描”部分开始解码图像的实际扫描。由于我们将主要处理YCbCr图像,因此我们可以假设将存在三个分量,它们的类型分别为1、2和3。让我们编写代码以解码此数据:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
我们向JPEG类添加了一个list属性,
quantMapping并定义了一种方法BaselineDCT,该方法对SOF部分中的所需数据进行解码,并将每个组件的量化表数量放入列表中quantMapping。当我们开始阅读“扫描开始”部分时,将利用这一点。这就是我们寻找照片的方式quantMapping:
Quant mapping: [0, 1, 1]
解码开始扫描
这是JPEG图像的“肉”,它包含图像本身的数据。我们已经到了最重要的阶段。我们之前解码的所有内容都可以视为一张有助于我们解码图像本身的卡。此部分包含图片本身(已编码)。我们读取该部分,并使用已解码的数据进行解密。
所有标记均以开头
0xff。该值也可以是扫描图像的一部分,但是如果此部分中存在该值,则其后总是和0x00。 JPEG编码器自动将其插入,这称为字节填充。因此,解码器必须删除这些0x00。让我们从包含此类功能的SOS解码方法开始,并摆脱现有的功能0x00。在扫描部分的图片中,没有0xff但这仍然是一个有用的补充。
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
以前,当我们找到标记时,我们手动搜索文件的结尾
0xffda,但是现在有了一个工具,可以系统地查看整个文件,我们将在操作符中移动标记搜索条件else。该函数RemoveFF00只是在找到其他东西而不是0x00after之后才会中断0xff。函数找到时0xffd9,循环中断,因此我们可以搜索文件的末尾而不必担心出现意外。如果运行此代码,则终端中将看不到任何新内容。
请记住,JPEG将图像分成8x8矩阵。现在我们需要将扫描的图像数据转换为比特流,并以8x8的块进行处理。让我们将代码添加到我们的类中:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
让我们开始将数据转换为比特流。您还记得相对于先前的DC元素将增量编码应用于量化矩阵的DC元素(其第一个元素)吗?因此,我们初始化
oldlumdccoeff,oldCbdccoeff并oldCrdccoeff与零个值,它们将帮助我们保持之前的DC元素的值的轨道,并且将0默认设置时,我们发现第一个DC元素。
该循环
for可能看起来很奇怪。self.height//8告诉我们可以将高度除以8 8多少次,宽度和相同self.width//8。
BuildMatrix将获得一个量化表并添加参数,创建一个逆离散余弦变换矩阵,并为我们提供Y,Cr和Cb矩阵。并且该功能DrawMatrix将它们转换为RGB。
首先,让我们创建一个类
IDCT,然后开始填写方法BuildMatrix。
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
让我们分析一下类
IDCT。提取MCU时,它将存储在attribute中base。然后,通过使用该方法回滚之字形扫描来转换MCU矩阵rearrange_using_zigzag。最后,我们将通过调用方法回退离散余弦变换perform_IDCT。
您还记得,DC表是固定的。我们将不考虑DCT的工作原理,这与数学而不是编程更相关。我们可以将此表存储为全局变量并查询值对
x,y。我决定将表及其计算放在一个类中,IDCT以使文本可读。转换后的MCU矩阵的每个元素乘以一个值idc_variable,我们得到Y,Cr和Cb值。
当我们添加方法时,这将变得更加清晰
BuildMatrix。
如果将之字形表修改为如下所示:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
您得到以下结果(请注意一些小工件):

而且,如果您有胆量,可以进一步修改曲折表:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
那么结果将是这样的:

让我们完成我们的方法
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
我们首先创建一个离散余弦变换反转类(
IDCT())。然后,我们将数据读入比特流,并使用霍夫曼表对其进行解码。
self.huffman_tables[0]分别self.huffman_tables[1]参考DC表的亮度和色度,self.huffman_tables[16]以及self.huffman_tables[17]参考AC表的亮度和色度。
在对比特流进行解码之后,我们使用一个函数来
DecodeNumber 提取新的经增量编码的DC系数,然后将其添加olddccoefficient以获得经增量编码的DC系数。
然后我们对量化矩阵中的AC值重复相同的解码过程。代码含义
0表示我们已经到达块结尾(EOB)标记,必须停止。此外,AC量化表的第一部分告诉我们我们有多少个前导零。现在,让我们记住有关编码序列长度的信息。让我们逆转此过程,并跳过所有许多位。在类中为IDCT它们明确分配了零。
解码MCU的DC和AC值后,我们转换MCU并通过调用反转锯齿形扫描
rearrange_using_zigzag。然后我们反转DCT并将其应用于解码后的MCU。
该方法
BuildMatrix将返回反DCT矩阵和DC系数的值。请记住,这仅是一个最小8x8编码单位的矩阵。让我们对文件中的所有其他MCU进行此操作。
在屏幕上显示图像
现在,让我们在方法中的代码
StartOfScan创建一个Tkinter Canvas,并在解码后绘制每个MCU。
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
让我们从功能
ColorConversion和开始Clamp。ColorConversion取Y,Cr和Cb值,然后通过公式将它们转换为RGB分量,然后输出汇总的RGB值。您可能会问,为什么还要添加128个?请记住,在使用JPEG算法之前,将DCT应用于MCU并从颜色值中减去128。如果颜色最初在[0.255]范围内,JPEG将把它们放在[-128,+ 128]范围内。解码时需要回滚此效果,因此我们将RGB添加128。至于Clamp拆包时,结果值可能超出范围[0.255],因此我们将其保持在此范围[0.255]。
在方法中
DrawMatrix我们针对Y,Cr和Cb遍历每个解码的8x8矩阵,并将每个矩阵元素转换为RGB值。转换后,我们canvas使用方法在Tkinter中绘制像素create_rectangle。您可以在GitHub上找到所有代码。如果您运行它,我的脸将出现在屏幕上。
结论
谁曾想到要露面,您将不得不撰写超过6,000字的说明。令人惊讶的是某些算法的作者多么聪明!希望您喜欢这篇文章。在编写此解码器时,我学到了很多东西。我认为编码简单的JPEG图像不需要太多的数学运算。下次您可以尝试编写用于PNG(或其他格式)的解码器。
附加材料
如果您对这些细节感兴趣,请阅读我用来撰写本文的材料以及一些其他工作: