你好居住者！如果没有计算机科学背景，您可能会称呼程序员为泥泞。对基础知识的自信掌握使您不必“重新发明轮子”，也不必在软件体系结构中构建有效的解决方案。所有这些消除了错误和测试和重构的过多成本。
当其他程序员在讨论近似极限时，是否感到不适应并不重要。即使是经验丰富的专家也会犯错，因为他们忘记了计算机科学。
为什么需要这本书
我（作者）的许多开发人员都来自各个领域。有些人接受了计算机科学方面的高等教育；其他人则学习摄影，数学，甚至从未毕业。
近年来，我注意到程序员出于多种原因越来越渴望学习计算机科学：
- 成为优秀的程序员；
- 在面试中回答有关算法的问题；
- 来满足他们对计算机科学的好奇心，或者最后不再后悔他们一次没有机会掌握这一学科。
这本书适合所有人。
许多人会在这里找到本身有趣的主题。我试图证明这种知识在真正的（非学术的）情况下是有用的。阅读本书之后，我希望您获得与学习计算机科学基础课程相同的知识，并学习如何应用它。
简而言之，本书的目的是通过对计算机科学的更好理解来帮助您成为更有技能和经验的程序员。我无法将20年的大学教学和专业经验融入一本书中……但是我会尽力而为。我希望您能在这里找到至少一个主题，您可以对这个主题说：“是的，现在我明白了”，并在您的工作中运用知识。
您在该版本中找不到的内容
这本书的意思是帮助读者更好地理解计算机科学并在实践中应用知识，而不是完全取代四年的学习。
特别是，这不是证明书。确实，在本书的第二卷中，考虑了证明方法，但是此处通常提供标准算法而没有证明。这个想法是让读者了解这些算法的存在，并学习如何使用它们而无需详细介绍。作为写给本科生和研究生的证明书，我强烈推荐Cormen，Leiserson，Rivest和Stein撰写的《算法导论》（作者通常分为以下几类：缩写CLRS）。
这也不是一本编程书籍：您将找不到有关何时使用int以及何时使用double的准则，也找不到任何关于循环的解释。希望读者能够理解用于描述算法的伪代码清单（本书中的所有程序均基于C语言以伪代码编写）。本书的目的是将计算机科学的概念与读者已经熟悉的编程技术联系起来。
10.动态编程
10.1。缺少字段问题
假设我们有一个n×n的棋盘缺少几个正方形。如何找到最大的k×k的一块板而又没有遗漏的字段？
如果您以前从未遇到过此类问题，请花几分钟时间编写解决方案并确定算法的执行时间。
面对这个问题，我推断如下。每个棋盘格字段都可以属于许多最大的区域，但是只有其中一个可以位于左上角。如果我用左上角最大的完整区域的大小标记每个框，则具有最大此类标记的字段将对应于所需的区域。
假设电路板以n×n矩阵表示，其中每个单元格包含1（如果存在相应的字段），如果包含则为0。如果当前单元格值为0，则对应的字段不存在并且不能成为连续段的一部分，因此不需要更改它。如果值为1，则可以用比位于下方和右侧的三个单元格的最小值大一的数字来代替它。
我们一次更改矩阵的每个单元格，包括检查单元格的值是否为零，检查最多三个单元格的值以及写入新的单元格值。这些操作每个都需要O（1）时间，因此处理整个棋盘格所花费的时间为
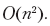
请注意，这是算法的线性执行时间，而不是二次执行时间-在棋board n上（假设n是字段总数，并且我们遵循通常的约定，n是输入数据量）字段（其中一些是缺少），因此算法花费的总时间与字段数成正比。如果我们将棋盘的大小更准确地表示为√n×√n，则得到n个字段，总执行时间为O（n）。
10.2。处理重叠的子任务
本节中使用的方法称为动态编程。当一个问题可以分为几个子任务时，将使用该子任务，每个子任务的解决方案将被使用多次。当问题分为子任务时，这种方法不同于“分而治之”的原则，这些子任务彼此独立地解决。在棋盘问题中，每个子问题都取决于其他三个问题的解决方案，并且保存了所有子问题的解决方案供以后使用。
动态编程通常通过构建表来完成，如上所示。这意味着要使用自下而上的方法来解决问题，我们首先要解决最小的子问题，然后逐步解决直到找到答案。另一种方法是备忘录，我们从头到尾进行操作，根据需要解决子问题，并将结果缓存起来以供重用。当您需要解决每个子问题（在我的棋盘示例中，有必要为棋盘的每个区域找到最大的完整区域）时，构建表是首选的选择，因为这种方法的成本比存储备忘录的成本低。如果不必解决解决方案领域中的某些子任务，则使用备注可以只解决那些确实需要的子任务。
关键点
分而治之涉及将一个任务划分为几个独立的子任务，而动态编程则意味着将一个任务划分为多个重叠的子任务。缓存每个子问题的解决方案，以供以后重用。
10.3。动态编程和最短路径
考虑找到最短路径的问题：对于给定的具有加权边缘的图，您需要找到从一个节点到另一个节点的成本最低的路径。
定义
边缘加权图是其中每个边缘都有自己的权重（成本）的图。从一个节点到另一个节点的路径成本由所有经过的边的成本之和确定。
假设我们在节点s和t之间找到一条包含第三个节点v的路径。那么从s到t的路径必须包含从s到v的最短路径，因为否则我们可以用更短的路径替换此段并减少从s到t的最短路径的长度，这与初始条件相矛盾（这是Bellman的最优性原理）。
( ) , . , . , .
, , .
寻找最短路径的问题是动态编程的引人注目的例子，因为子结构的最佳属性直观地很明显-很明显，从A点到C点再经过B点的最快方法也是从A点到B点以及从点到点的最快方法。 B到C点。基于此原理的算法数量包括Bellman-Ford方法，该方法可以找到从起点到图形的任何顶点（或从图形的任何顶点到终点）的最短路径，以及Floyd-Warshall方法-借助其帮助计算每对图顶点之间的最短路径。在这两种情况下，其想法都是从节点附近的一小部分子节点开始，然后使用已经发现的节点来逐渐扩展该集合以计算新距离。
10.4.
10.4.1. Git merge
通常用来演示动态编程的另一个任务是找到最长的公共子序列。任务是为两个给定的字符串A和B查找两个字符串中出现的最长序列，同时保持字符序列。字符串不必排成一行；例如，如果A = {acdbef}和B = {babdef}，则{adef}将是它们的常见子序列。
合并Git中的更改（合并）时，它将搜索主分支和工作分支的最大公共子序列。删除存在于母版中但不存在于最大公共子序列中的字符；在工作分支中但不在此子序列中的字符被添加到master。
10.4.2. LATEX
LATEX文件准备系统通常用于创建技术文件。打字系统的任务之一是同时使文本左右对齐。为此，将单词和字符之间的间距拉长或缩小，以便所有行都具有相同的长度。对齐文本的另一种方法是换行最后一个单词，以使单词的一部分出现在下一行。 LATEX（从技术角度来看，TEX文本输入系统几乎可以完成所有工作； LATEX建立在TEX之上。出于简化的原因，在此使用LATEX）试图找到最佳的换行点，以使文本看起来更漂亮。如果失败，则一行中的多行将以单词连字符结尾，否则不同行中的单词之间的距离将有所不同。LATEX有一组评估对齐失败的规则。该程序试图找到“最差”选项。
如果段落中有n个可能的换行符，则
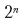可以使用多种选项来中断文本。每个断点选择的“失败”取决于之前选择的断点。因此，我们再次有重叠的子任务。动态编程技术的使用减少了执行时间
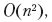，可以通过其他方法将其缩短。
»有关这本书的更多详细信息，请访问出版商的网站
»目录
»摘录
给居住者的优惠券可享受25％的折扣-计算机科学
在为该书的纸质版本付款后，会向该电子邮件发送一本电子书。