数学的未来是什么？
- 在1990年代，计算机开始下象棋的能力比人类更好。
- 在2018年，计算机比人类更擅长于玩围棋。
- 2019年，人工智能研究员Christian Szegedy告诉我，在10年内，计算机将比人类更好地证明定理。
当然，他可能是错的。也许他是对的。
我相信以下内容：十年后，计算机将帮助我们在早期研究生水平上证明沉闷定理。数学的哪些领域？取决于谁参与这一领域的研究。
人工智能的典型模式是这样的：首先，它非常愚蠢，然后突然变得更聪明。自然的问题是：什么时候发生相变而人工智能突然变得非常聪明？答：没人知道。清楚的是，参与这一研究领域的人越多，发生的越早。
什么是证明？
如果您问优秀的学生，研究数学家和计算机，那是什么证明，他们的答案是什么？优秀学生和计算机的答案将一致，如下所示：
证明是陈述的逻辑顺序，由所选系统的公理，推理规则和较早证明的定理组成，最终导致证明被证明。当然，研究数学家的答案不会那么理想化。对于数学家来说，证明的定义就是其他有经验的数学家认为的证明。或《数学或发明年鉴》上接受出版的内容。
但是，这有一个小问题。以下屏幕截图摘自《世界数学年鉴》，这是世界上最负盛名的数学期刊之一。
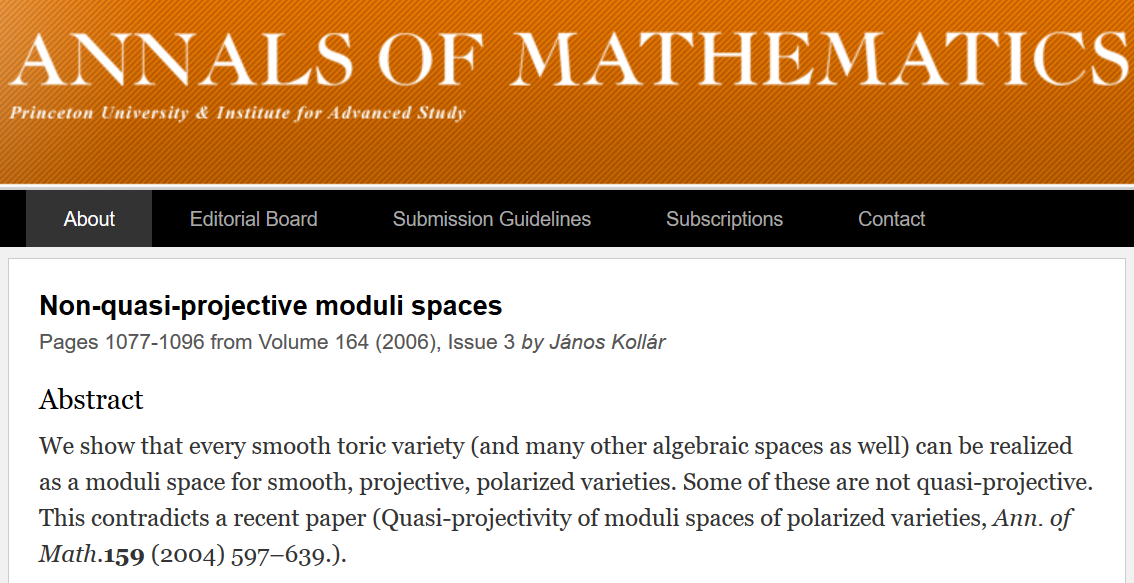
第二篇文章与第一篇矛盾。作者在注释中公开地写了这个。据我所知，《数学年鉴》从未发表过对这些著作的任何反驳。有经验的数学家认为哪项工作是正确的？如果您在此领域工作，则只能找到有关此信息。
输出量：在现代数学中，关于某物是否为证明的观点随时间而改变（例如，它可以从“是”变为“不是”）。
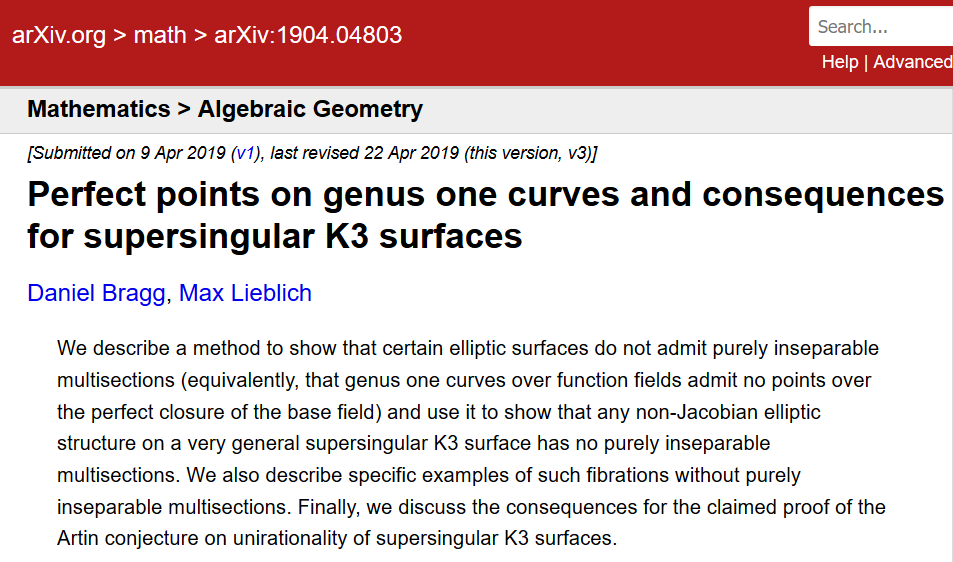
这篇简短的2019年文章表明，2015年发表在发明发明上的另一篇重要文章严重依赖虚假引理。直到2019年才注意到这一点，尽管事实上在2016年人们举办了研讨会来研究这项重要工作。
弗朗西米尔·沃夫斯基（Vladimir Voevodsky）是为数学基础做出贡献的菲尔兹奖获得者，他写道：“如果受到人们信任的作者写了一个技术上复杂的论点，难以证实，但与其他正确论点相似，那么这种论点就永远不会任何事情都将被详细检查。”
发明人从未发表过对2015年论文的反驳。
结论：重要的数学有时被证明是错误的。此外，将来我们肯定会看到对已发表证据的更多反驳。
也许我在p-adic Langlands计划中所做的工作是基于错误的结果。或者，更乐观的是，正确的结果，但尚无完整的证据。
如果我们的研究不可重复，我们可以称之为科学吗？我有99.9％的决心确保Langlands的p-adic程序不会被人类用来做任何有用的事情。如果我的数学工作无济于事，并且保证100％正确，那只是浪费时间。... 因此，我决定停止研究，而专注于在计算机上测试“著名的”数学。
在2019年，Balakrishnan，Dogra，Mueller，Tuitman和Vonk在两个变量中找到了某个四度方程的所有有理解。明确地：
该计算在算术中具有重要的应用。该证明在很大程度上依赖于使用快速，未引用算法的岩浆（封闭源系统）中的计算。将所有计算移植到像sage这样的开源系统上将很困难。但是，没有人打算这样做。
因此，一些证据仍然隐藏。也许它将永远隐藏。这是科学吗？
数学上的差距
- 1993 . .
- 1994 , .
- 1995 , , . , , , . , , , .
收到数学文章进行审阅的审稿人应该怎么做？有人认为，审稿人的工作是“确保本文使用的方法足够强大，足以证明论文的主要结果。”
如果方法很强但作者却不怎么办？当我们的证据不完整时，就会出现这种情况。这就是关于我们的定理是否得到实际证明的争论。这根本不是我们教学生数学的方式。
当然，专家知道哪些文献可以信任，哪些不能。但是我是否必须成为专家才能知道我可以信任哪些文献？
数学上的巨大差距
展览A
简单有限群的分类。专家声称，我们对简单的有限组具有完整的分类。我相信专家。
- 1983年，专家宣布了分类证明。
- 1994年，专家发现了一个错误（但是，我们不让大象飞起来吗？）
- 2004年，出版了1000多页的作品。现场专家阿施巴赫（Aschbacher）声称该错误已得到纠正，并宣布了计划发行12卷完整证据的计划。
- 2005年，仅发行了12卷中的6卷
- 2010年，仅发行了12卷中的6卷
- 2017年，仅发行了12卷中的6卷
- 2018年，第7卷和第8卷出版，并注意该出版物将于2023年完成。
领导该项目的三人中，有一人死亡。另外两个超过七十。
展览B
阿贝尔曲面的潜在模块化。一年前，我杰出的研究生托比·吉（Toby Gee）和三位合著者发表了285页的预印本，其结果是，完全真实领域中的阿贝尔表面可能是模块化的。
他们的证明引用了三份未发表的预印本（一份于2018年，一份于2015年，一份于1990年代），一份2007年的互联网备忘录，一份未发表的德语论文，以及一篇其主要主张后来被驳回的论文。此外，在第13页上，我们看到以下文本：
, Arthur’s multiplicity formula GSp4, [Art04]. , , [GT18], , [Art13] [MW16a, MW16b]. , twisted weighted fundamental lemma, [CL10], . , [A24], [A25], [A26] [A27] [Art13], .我们可以诚实地说这是科学吗？
链接[CL10]如下所示：
我的研究生和合著者所需要的作品从未发表过。该陈述很可能是正确的。甚至可以证明。
这些是[Art13]中引用的链接：
去年，我向Arthur询问了这些链接，他告诉我尚未完成任何工作。当然，吉姆·亚瑟是个天才。他赢得了许多著名的奖项。但是他也已经75岁了。
展览C
Gaitsgory – Rozenblyum。无休止的类别最近越来越流行。随着时间的推移，它们将变得更加重要。菲尔兹奖获得者彼得·斯科尔兹（Peter Scholze）的作品无休止。
Jacob Lurie写了1000多页的有关
-分类，并在我的工作中包含很多细节。 Gaitsgory – Rozenblyum希望获得类似结果
-categories，但省略了许多参数以节省时间。 “遗漏的证据将出现在其他地方。”
我问盖茨哥里，多少钱不见了。他回答说大约是100页。我问卢里，他对此有何看法。他回答说：“数学家在忽略细节方面有多大的适应性。”
数学运算太快了吗？如果我是“专家”，我是否应该相信完全真实领域上的阿贝尔曲面可能是模块化的？老实说，我已经不认识自己了。
上周我在卡内基梅隆大学的一次会议上，马库斯·拉贝（Markus Rabe）告诉我，谷歌正在开发一个程序，该程序将翻译arxiv.org的数学预印本变成适合计算机验证的语言。最近，我还看到了一些工作，该工作依赖于我的学生的一篇文章，但并未提及[Art13]中缺少100页的任何内容。
最后的错误
这是一个非常有趣的例子。原始作品发表在J. Funct。肛门在2013年。工作中存在很大错误（另一个方向是不平等的）。该错误是S. Gouezel在2017年发现的，当时Gouezel使用计算机化的证明检查程序（Isabelle）正式确定了一个论点。
Gouezel和原始作品的作者提出了一个新的论点。新工作不需要审查。计算机检查了100％的新参数。结果证明该方法足够强大，可以证明该定理。 “证明”是指经典的，“纯粹的”证明定义，即我们教给学生的定义。证明的每个细节都可供读者使用。科学是可复制的。这是我们教给学生的数学。这是数学。
以下是我认为是数学的其他示例：
- 学生或硕士水平的典型证明
- 数以万计的数学家已经充分记录和研究了重要结果的典型100年历史证明
- Gonthier，Asperti，Avigad，Bertot，Cohen，Garillot，Le Roux，Mahboubi，O'Connor，Ould Biha，Pasca，Rideau，Solovyev，Tassi和Feith-Thompson定理的泰里的正式证明。
- 下列数学家的正式著作权证明：哈尔斯，亚当斯，鲍尔，达塔当，哈里森，特隆·勒昂，卡里斯基，马格隆，麦克劳克林，唐达·阮，特朗·光阮，尼普科，奥布阿，普雷索，鲁特，索洛维耶夫，安·霍伊·泰塔，Trung Nam Tran，Diep Thi Trieu，Urban，Ky Khac Vu和Zumkeller的开普勒猜想证明。
演讲文本到此结束，因为Kevin进入了他的主要部分：由Microsoft Research的Leo de Moura开发的Lean中的数学证明的形式验证。不幸的是，幻灯片中未包含示例。
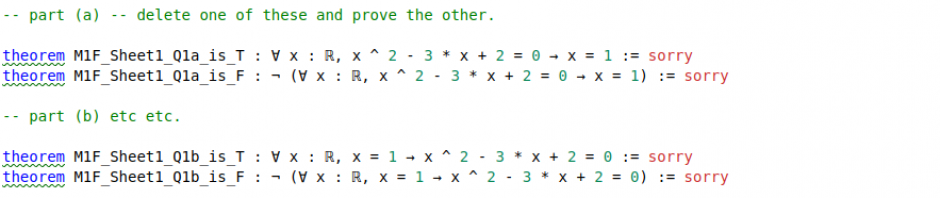
作者非常热衷于对数学证明进行形式验证，并在我强烈推荐的有关该主题的Xena博客上非常有意思。