大家好！我已经一百年没有写过Habr了，但是现在已经到了。今年春天，我在Mail.ru Group的MADE大数据学院教授了高级ML课程；似乎听众喜欢它，现在我被要求写的不是广告宣传，而是关于课程内容之一的教育性宣传。这个选择几乎是显而易见的：作为复杂概率模型的一个例子，我们讨论了一种非常相关的（似乎是……但稍后会更多）流行病学SIR模型，该模型可以模拟疾病在人群中的传播。它具有一切：通过Markov Monte Carlo方法进行近似推理，使用Viterbi随机算法隐藏Markov模型，甚至仅存在数据。



在这个主题下，只有一个小困难出现了：我开始写自己在讲课上实际讲到的内容...并以某种方式迅速而难以察觉地积累了二十页文本（包括图片和代码），但仍然没有完成了，并且完全不是独立的。而且，如果您以一种清晰的方式告诉所有内容，使之从“零”（当然不是绝对零）开始，那么您可以写一百页。因此，总有一天我一定会写它们，但是现在我提请您注意SIR模型的第一部分，其中我们只能提出一个问题，并从其生成方面描述该模型-如果受尊敬的公众有兴趣，那么将有可能继续。

SIR模型：问题陈述

我爱我的朋友，他们也爱我，

我们尽我们所能。

只是因为我们真的很在乎，

无论我们得到什么，我们都会分享！



汤姆·勒勒。我从艾格尼丝那里得到的

因此，让我们弄清楚。非正式地，SIR模型的基本假设如下：

• 有一定数量的人可以在其中行走一些可怕的病毒；
• 最初，病毒以一种或另一种方式进入人群（例如，第一个生病的人出现），然后人们彼此感染。
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

为简单起见，我们将假定那些患病的人总是会产生免疫力，并且将其排除在自然界的病毒循环之外。因此，这些状态之间的转换只能是从左到右：易感→已感染→已恢复。



实际上，任务是训练此模型，即从数据中了解有关感染过程参数的一些信息。很容易理解数据的样子-它只是每个时间点的已感染注册人数，我们将用向量表示$$$\boldsymbol{y}$... 例如，当我在关于冠状病毒的课程中做功课时（但是，关于其他模型），俄罗斯的数据如下所示：

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

但是这个模型的参数是什么，它们如何相互连接以及如何训练它们，尤其是在如此小的数据集上，是一个更严重的问题。



总的来说，我将遵循工作的总体轮廓（Fintzi等人，2016年），其中针对SIR，SEIR及其某些变体构建了MCMC算法。但是与（Fintzi等人，2016）相比，我将大大简化模型及其表示。主要的简化是，我们将考虑离散时间，而不是在原始工作中考虑的连续时间，也就是说，而不是在某个时候生成“感染”和“恢复”形式的事件的连续过程，我们将考虑人们经历了一系列离散的时间点$$$t=1,\ldots,T$... 这种简化将使我们首先摆脱许多技术难题，其次，从一般的Metropolis-Hastings算法转移到Gibbs采样算法，也就是说，不像需要进行计算那样计算Metropolis比率（Fintzi等等人，2016年）。如果您不明白我刚才所说的话，请不要担心：我们今天将不需要此内容，如果还有下一部分，我将在此处进行解释。



我们将分别用S，I和R表示SIR模型的状态以及一个人的状态$$$i$ 在这一刻 $$$t$ -对面 $$$x_i^{(t)}\in\{S, I, R\}$... 同时，我们将立即为尚未生病的患者总数引入变量。$$$S^{(t)}$生病 $$$I^{(t)}$ 并恢复 $$$R^{(t)}$ 在这一刻 $$$t$... 我们将拥有的总人数$$$N$所以对于任何人 $$$t$ 将被执行 $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... 而且，正如我上面所写，$$$y^{(t)}$其中有登记（经过测试）的病人。



模型的未知参数是$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$哪里：

• $$$\boldsymbol\pi$ -案件的初步分配；换一种说法，$$$x^{(1)}_j\sim \boldsymbol{\pi}$ 每个 $$$j$; 在我们简化的模型中，我们不会训练$$$\boldsymbol\pi$，但我们只会在第一时间记录1-2个案例；
• $$$\rho$ -在一般人群中找到被感染者的可能性，即一个人 $$$x_j$ 在此刻 $$$t$什么时候 $$$x_j^{(t)}=I$，将通过测试检测并注册到数据中 $$$y^{(t)}$; 换句话说，对于每个生病的人，我们掷一枚硬币以确定测试是否可以找到它，因此当前项目为$$$y_t$ 具有参数的二项式分布 $$$I^{(t)}$ 和 $$$\rho$：

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ -病人在一个时间步中恢复的概率，即从状态过渡的概率 $$$I$ 处于状态 $$$R$;

和 $$$\beta$ -这是最有趣的参数，显示在一个时间段内一名感染者被感染的可能性。这意味着在该模型中，我们假设人口中的所有人彼此“交流”（此处的“交流”表示接触足以传播疾病；冠状病毒主要通过空气中的飞沫传播，但是当然可以建模和传播其他疾病的传播；例如，参见题词），被感染的可能性取决于现在感染了多少，即取决于什么$$$I^{(t)}$... 我们将假设最简单的模型，其中一个感染者的感染概率为$$$\beta$，并且所有这些事件都是独立的，这意味着保持健康的可能性为

$$

$$(1-\beta)^{I^{(t)}}.$$

这些假设实际上有很多要讨论。我个人认为，这里最令人惊讶的是$$$y^{(t)}$... 抛硬币以检测到感染者的可能性是绝对正常的，但是在每个步骤中再次抛硬币是不现实的，也就是说，我们可以“忘记”已经检测到的感染者。结果，SIR模型可以（并且经常确实）产生一个完全非单调的序列$$$\boldsymbol{y}$;这很奇怪，但是似乎对结果影响不大，更现实地建模此过程将更加困难。



此外，很明显，此模型适用于封闭的人群，每个人都与每个人“沟通”，因此，对于参数N为一亿的俄罗斯或对于参数为一千万的莫斯科，启动该模型是没有意义的。计算上将无法正常工作）。 SIR模型扩展和扩展的重要领域致力于此：如何添加更现实的相互作用和可能的感染图;我们可能会在最后的最后一篇文章中谈论这一点。



但是，通过所有这些简化，现在，使用上述参数，我们可以写出状态之间转换的概率矩阵。这些概率（更确切地说，是被感染的概率）取决于总体的统计数据。让我们指定所有人的状态向量$$$x_j$，跨 $$$\boldsymbol{x}_{-j}$，并将相同的符号扩展到所有其他变量；例如，$$$I_{-j}^{(t)}$ 一次感染的数量 $$$t$， 更何况 $$$x_j$... 然后，从$$$x_j^{(t-1)}$ 在 $$$x_j^{(t)}$ 我们得到

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

在所有其他情况下

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

可以用转移概率矩阵的形式（行和列的顺序是自然的，SIR）更清楚地写出相同的内容：

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

对于熟悉马尔可夫链和马尔可夫模型的读者来说，这似乎只是一个隐含的马尔可夫模型：存在一个隐含状态，每个隐含状态都有明显的可观察变量分布，过渡实际上是马尔可夫状态，也就是说，下一个隐含状态仅取决于前一个隐含状态。正如他们所说，有一个警告：过渡概率不能被认为是恒定的，它们随着变化而变化 $$$I^{(t)}$这是该模型的一个极其重要的方面，不能被抛弃。



因此，与通常的隐式马尔可夫模型相比，此模型的推理突然变得困难得多（尽管也不总是这样）。但是，尽管结论较为复杂，但仍受人的思想约束-在以后的安装中（如果有的话），我将告诉您。就今天而言，几乎足够了-现在让我们稍微放松一下，尝试暂时性地使用此模型。

数据生成示例

作为伟大的鉴赏家和专家，一个

内向的人被隔离。

***

“我不能在家工作，”

蜜蜂试图向蠕虫解释。

***

卡加诺夫开玩笑而死。

当然，我为他感到非常抱歉，...



Leonid Kaganov。隔离区

如果模型的参数已知，并且您只需要生成疾病在人群中的传播将如何发展的轨迹，那么SIR就没有什么复杂的了。下面的代码根据我们的模型生成了一个人口示例；我编码为$$$S=0$， $$$I=1$， $$$R=2$... 正如我警告过的，为简单起见，我会假设目前$$$t=0$ 人口中恰好有一个病人，然后继续下去。

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

该代码不仅给出了实际数据 $$$\boldsymbol{y}$还有“真实的”统计 $$$S^{(t)}$， $$$I^{(t)}$， $$$R^{(t)}$因此它们可以可视化。我们开始做吧; 用于参数$$$N=100$， $$$T=20$， $$$\rho=0.1$， $$$\beta=0.2$， $$$\mu=0.3$您会得到类似的结果：







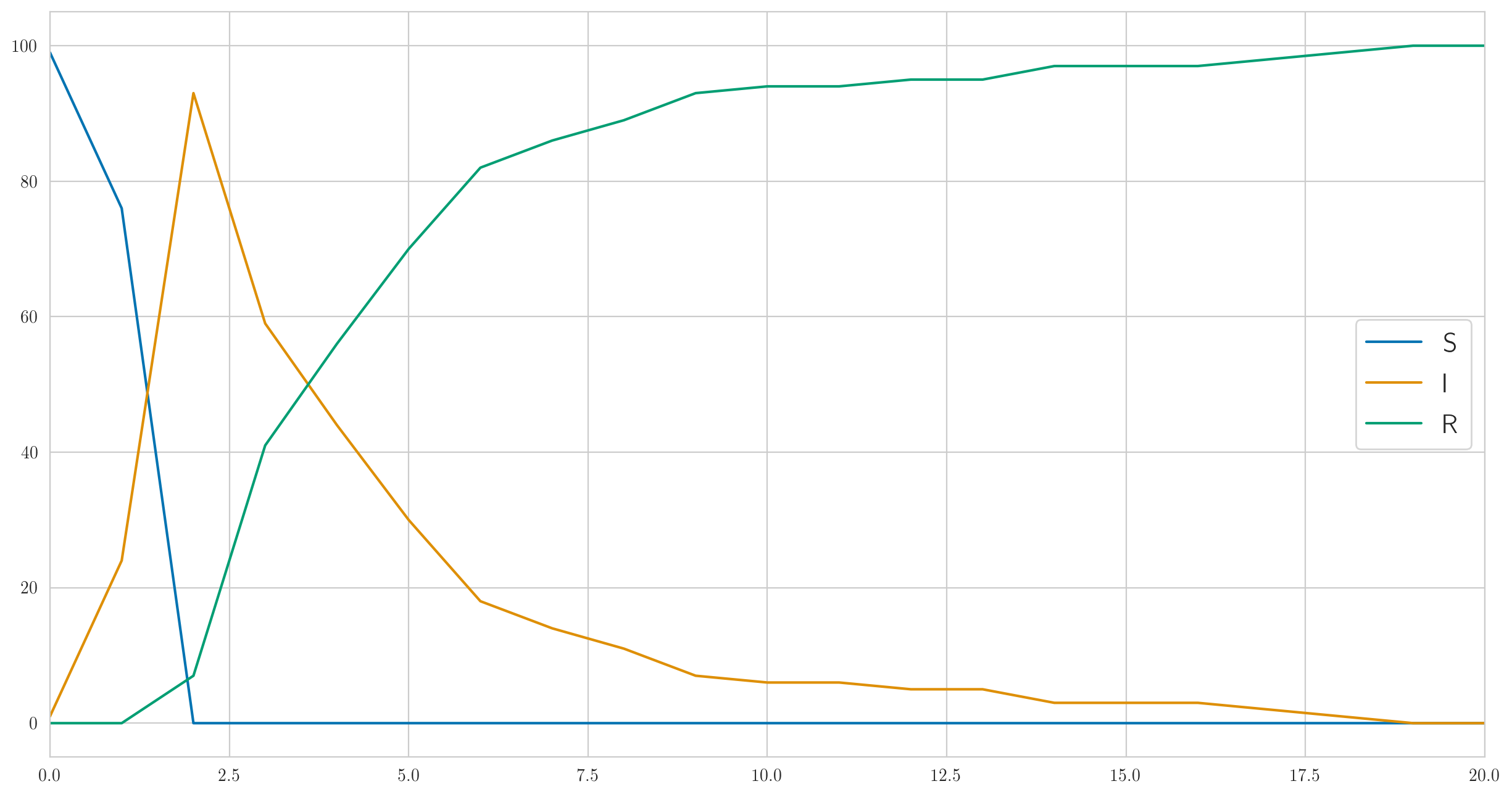
如您所见，在本示例中，每个人都会很快生病，然后慢慢开始好转。实际观察到的关于病人的数据如下所示：

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 0 1 0 0]

注意，如上所述，这里没有单调性。



但这当然不是唯一可能的行为。我选择了上述参数，以使感染足够快，并且该疾病几乎立即覆盖了我们测试人群中的所有一百人。如果你这样做$$$\beta$ 较小的，例如 $$$\beta=0.01$，那么感染的速度就会慢得多，甚至每个人都没有时间在最后一个病人康复之前就无法生病。像这样：







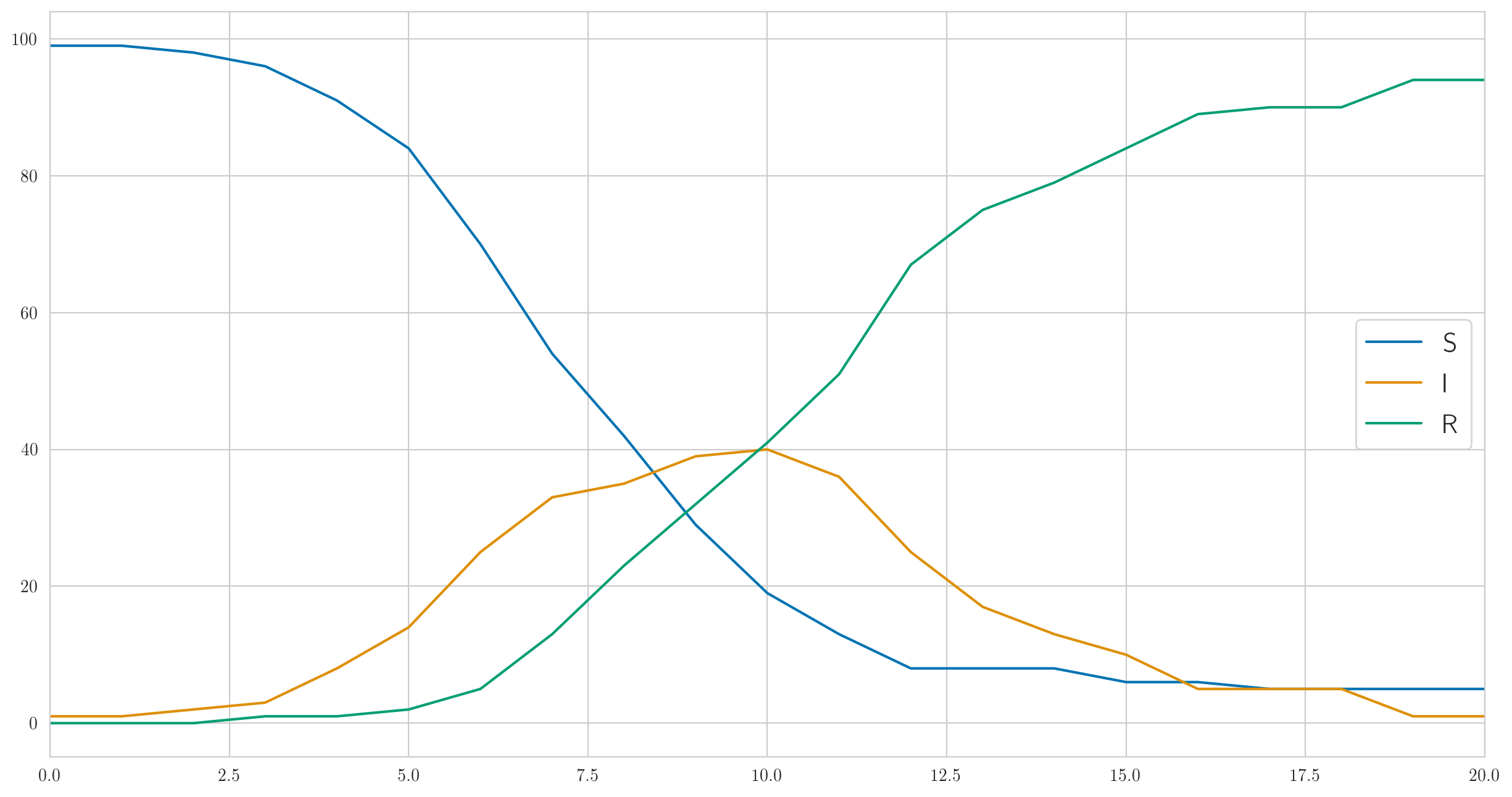
检测到的病例数也完全不同：

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

有可能更进一步“扼杀”这种疾病。例如，让我们离开$$$\beta=0.01$但是放 $$$\mu=0.5$，也就是说，在每个时间间隔内，每个患病者都有机会恢复0.5（最终，这是合乎逻辑的：无论他是否会康复）。这样一来，每100人中只有50-60人会患上这种可怕的病毒；曲线如下所示：

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

但是，总的来说，无论如何，总的情况看起来是差不多的：首先是指数增长，然后是饱和。唯一的区别是最后一个运营商是否有时间在所有人重新启动之前恢复。



好了，该总结中期结果了。今天，我们已经看到了最简单的流行病学模型之一。尽管有很多过分简化的假设，但即使采用这种形式，SIR模型仍然非常有用。事实是，它的大多数扩展都是相当简单的，不会改变问题的一般本质。因此，如果我们继续，在下一个系列中，我将讨论如何训练SIR模型。但是，这将涉及许多有趣的事情，以至于它也可能不在一篇文章中。直到下一次！