我们了解并创造
文章前的好消息是:不需要很高的数学技能和阅读能力(希望!)。
免责声明:本文代码的一部分,就像以前的一个,是一个调整,补充和测试翻译。我感谢作者,因为这是我最初的代码经验之一,此后我被更多的洪水淹没。希望我的改编对您同样有用!
所以走吧!
结构是这样的:
- 什么是马尔可夫链?
- 连锁店运作方式的一个例子
- 过渡矩阵
- 带有Python的Markov链模型-数据驱动的文本生成
什么是马尔可夫链?
马尔可夫链是随机过程理论中的一种工具,由n个状态的序列组成。在这种情况下,仅当状态严格彼此相邻时,才创建链的节点(值)之间的连接。仅
记住胖字,让我们推断马尔可夫链的性质:该链
中某个新状态的概率仅取决于当前状态,而在数学上并未考虑过去状态的经验=>马尔可夫链是没有记忆的一条链。
换句话说,新含义总是与直接由手柄握住的含义产生共舞。
连锁店运作方式的一个例子
就像文章的作者一样,我们从中借用了代码实现,让我们采用随机的单词序列。
开始-人造-皮大衣-人造-食品-人造-意大利面-人造-皮大衣-人造-结束
让我们想象一下这实际上是一首伟大的诗歌,我们的任务是模仿作者的风格。(但是,这样做当然是不道德的)
如何决定?
我想做的第一件事就是计算单词的出现频率(如果我们要使用实时文本来执行此操作,首先应该进行规范化-将每个单词带入引理(词典形式))。
开始== 1
人工== 5
皮大衣== 2
意大利面== 1
食物== 1
结束== 1
记住我们有一个马尔可夫链,我们可以根据前面的图形来绘制新单词的分布图

:
- 毛皮大衣,食物和面食的状态100%表示人工状态p = 1
- “人造”状态可能导致4种情况发生的可能性相等,并且进入人造毛皮大衣状态的可能性高于其他3种情况
- 最终状态无处可去
- 状态“开始” 100%需要状态“人工”
它看起来很酷而且合乎逻辑,但是视觉美还不止于此!我们还可以构造一个转换矩阵,并在其基础上用以下数学正义来吸引人:

俄语中的意思是“某事件k的一系列概率之和,取决于i ==事件k的概率的所有值的总和,取决于状态i的发生,其中事件k == m + 1,事件i == m(也就是说,事件k与i总是相差1)”。
但首先,让我们了解什么是矩阵。
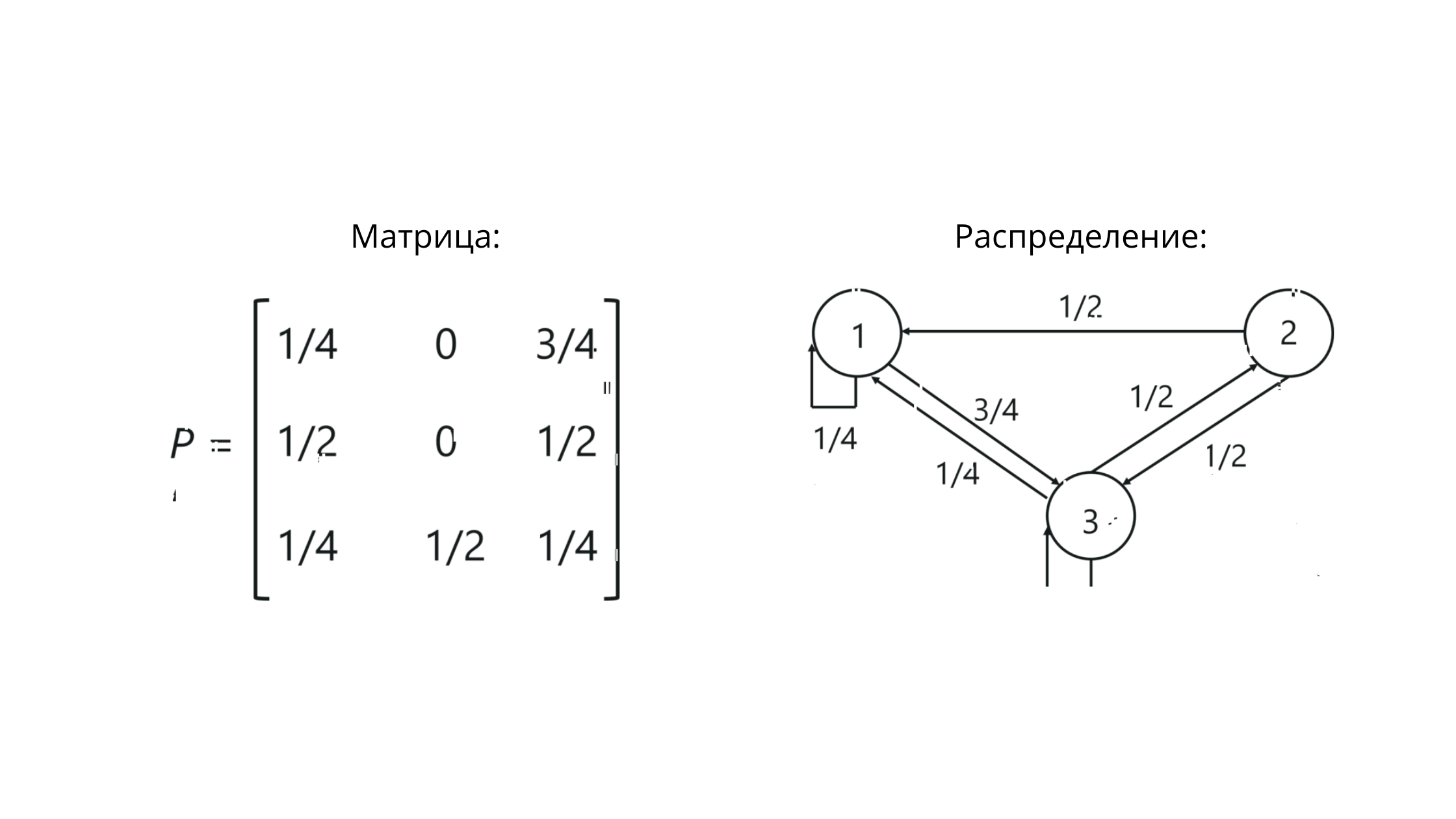
过渡矩阵
在处理马尔可夫链时,我们正在处理一个随机转移矩阵-一组向量,其中的值反映了渐变之间的概率值。
是的,是的,听起来像是听起来。
但这看起来并不那么可怕:

P是矩阵的表示法。列和行的交点处的值反映了状态之间转换的可能性。
对于我们的示例,它将看起来像这样:

请注意,该行中的值之和== 1.这意味着我们已经正确构建了所有东西,因为随机矩阵行中的值之和必须等于1。
没有人造皮草外套和浆糊的
裸露示例:一个甚至裸露的示例是以下内容的身份矩阵:
- 无法从A返回B以及从B-返回A的情况[1]
- 从A到B的过渡是可能的情况[2]

Respecto。理论完成。
我们使用Python。
使用Python基于Markov链的模型-基于数据生成文本
步骤1
导入相关的工作包并获取数据。
import numpy as np
data = open('/Users/sad__sabrina/Desktop/1.txt', encoding='utf8').read()
print(data)
, , , , ( « memorylessness »). , , , , , , ; .., , .
不要只关注文本的结构,而要注意utf8编码。这对于读取数据很重要。
步骤2
将数据分成单词。
ind_words = data.split()
print(ind_words)
['\ufeff', '', '', '', '', ',', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', ',', '', '', '', '', '(', '', '', '«', 'memorylessness', '»).', '', ',', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', '', '', ',', '', '', '', '', '', '', '', ',', '', '', ',', '', '', '', ';', '..,', '', '', '', '', ',', '', '', '', '', '', '', '.']步骤3
让我们创建一个链接单词对的函数。
def make_pairs(ind_words):
for i in range(len(ind_words) - 1):
yield (ind_words[i], ind_words[i + 1])
pair = make_pairs(ind_words)该函数的主要细微差别在于使用yield()运算符。它可以帮助我们满足Markov链接标准-无记忆存储标准。使用yield,我们的函数将在迭代(重复)时创建新的对,而不是存储所有内容。
在这里可能会产生误解,因为一个词可以变成不同的词。我们将通过为我们的函数创建一个字典来解决这个问题。
第4步
word_dict = {}
for word_1, word_2 in pair:
if word_1 in word_dict.keys():
word_dict[word_1].append(word_2)
else:
word_dict[word_1] = [word_2]这里:
- 如果我们已经有字典中成对的第一个单词的条目,则该函数将下一个潜在值添加到列表中。
- 否则:创建一个新条目。
步骤5
让我们随机选择第一个单词,然后使用islower()字符串方法设置while条件,以使单词真正随机,如果字符串包含小写字母,则该条件满足True,允许存在数字或符号。
在这种情况下,我们将单词数设置为20。
first_word = np.random.choice(ind_words)
while first_word.islower():
chain = [first_word]
n_words = 20
first_word = np.random.choice(ind_words)
for i in range(n_words):
chain.append(np.random.choice(word_dict[chain[-1]]))步骤6
让我们开始随机的事情!
print(' '.join(chain))
; .., , , (join()函数是用于处理字符串的函数。在括号中,我们为行(空格)中的值指定了一个分隔符。
文字……听起来像机器,而且几乎合乎逻辑。
PS正如您可能已经注意到的那样,马尔可夫链在语言学中很有用,但它们的应用超出了自然语言处理的范围。您可以在这里和这里熟悉其他任务中链的使用。
PPS如果事实证明您对我的代码习惯不甚了解,请附上原始文章。一定要在实践中应用该代码-它“运行并生成”时的感觉很充实!
我正在等待您的意见,并且很高兴对本文发表建设性意见!