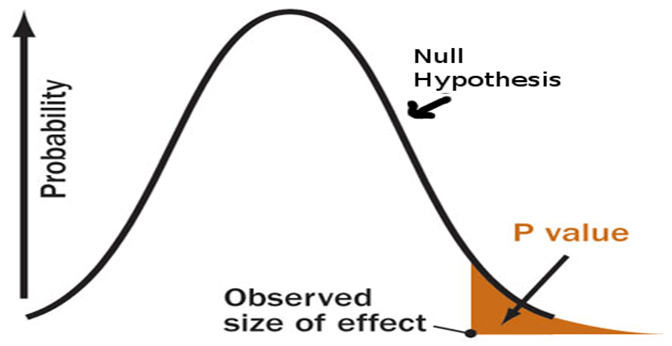
当时,我对p值,假设检验甚至统计意义一无所知。
我决定在Google上搜索“ p-value”一词,而我在Wikipedia上发现的内容使我更加困惑……
在检验统计假设时,给定统计模型的p值或概率值是以下可能性:如果无效假设为真,则统计摘要(例如,两个比较组之间差异的样本均值的绝对值)将大于或等于实际观察到的结果。干得好,维基百科。
-维基百科
好的。我不明白p值的实际含义。
当我深入研究数据科学领域时,我终于开始了解p值的含义以及在某些实验中p值可以用作决策工具的一部分的情况。
因此,我决定在本文中解释p值,以及如何将其用于假设检验中,以使您更好,更直观地理解p值。
同样,我们也不能错过对其他概念和p值定义的基本理解,我保证我将使这种解释变得直观,而不会向您暴露我遇到的所有技术术语。
本文共有四个部分,从构建假设检验到了解p值并将其用于决策过程中,您可以全面了解。我强烈建议您仔细阅读所有内容,以详细了解p值:
- 假设检验
- 正态分布
- 什么是P值?
- 统计学意义
应该会很好玩。
开始吧!
1.检验假设
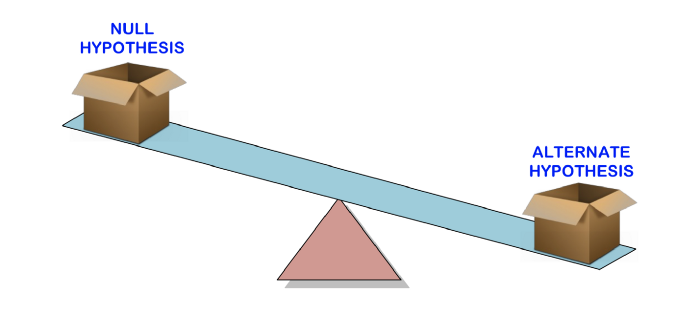
在讨论p值的含义之前,让我们先看一下假设检验,其中p值用于确定结果的统计显着性。
我们的最终目标是确定结果的统计意义。
统计意义基于以下三个简单的想法:
- 假设检验
- 正态分布
- P值
假设检验用于使用样本数据来检验关于总体的陈述(无效假设)的有效性。另一种假设是,如果原假设被证明是错误的,您会相信。
换句话说,我们将创建一个声明(无效假设),并使用样本数据来检查该声明是否有效。如果陈述不正确,我们将选择另一种假设。一切都非常简单。
为了确定索赔是否有效,我们将使用p值权衡证据的强度,以查看其是否具有统计意义。如果证据支持替代假设,那么我们将拒绝原假设并接受替代假设。下一节将对此进行解释。
让我们使用一个示例来使这个概念更清楚,并且在整个本文中,将使用该示例来介绍其他概念。
例。假设一家比萨店声称平均交货时间为30分钟或更短,但您认为它比它声称的要长。因此,您进行假设检验并随机选择交货时间以检验索赔:
- — 30
- — 30
- , , — — , .
在我们的案例中, 我们将使用单向测试,因为对我们来说,平均交付时间超过30分钟才是很重要的。我们不会从另一个方向考虑这种可能性,因为平均交付时间小于或等于30分钟的后果更为可取。在这里,我们要检查平均交货时间是否超过30分钟。换句话说,我们想看看比萨店是否欺骗了我们。
检验假设的常见方法之一是使用Z检验。我们在这里不做详细介绍,因为我们想在更深入地研究之前更好地了解表面上正在发生的事情。
2.正态分布
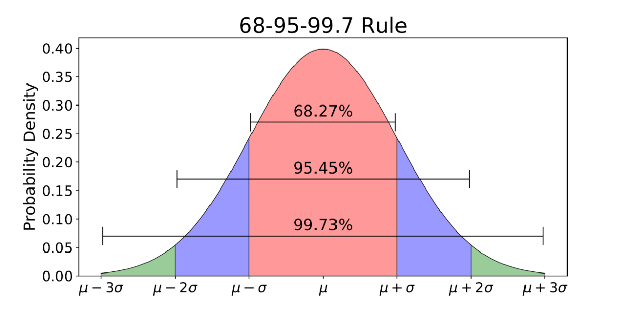
正态分布是用于查看数据分布的概率密度函数。
正态分布具有两个参数,均值(μ)和标准偏差,也称为sigma(σ)。
平均是分布的主要趋势。它定义了正态分布的峰值位置。标准偏差是变异性的量度。它确定值倾向于下降到平均值的距离。
正态分布通常与68-95-99.7规则相关(上图)。
- 68%的数据在平均值(μ)的1个标准偏差(σ)内
- 95%的数据在平均值(μ)的2个标准偏差(σ)内
- 99.7%的数据在平均值(μ)的3个标准偏差(σ)内
还记得我一开始就谈到的希格斯玻色子的五个西格玛门槛吗?5 sigma约占科学家确认希格斯玻色子发现之前必须接收的数据的99.99999426696856%。这是一个严格的阈值设置,以避免任何可能的错误信号。
凉。现在,您可能想知道,“正态分布与我们之前的假设检验有何关系?”
由于我们使用Z检验来检验假设,因此我们需要计算Z分数(将在我们的检验统计信息中使用),即与数据点均值的标准偏差数。在我们的案例中,每个数据点都是我们收到的披萨交付时间。 请注意,当我们计算每个比萨饼交货时间的所有Z分数并绘制如下所示的标准正态分布曲线时,当我们通过减去平均值并除以标准化变量时,X轴上的单位将从分钟变为标准偏差的单位其标准偏差(请参见上面的公式)。 检查标准钟形曲线很有用,因为我们可以将测试结果与具有标准偏差的标准化单位的“正常”总体进行比较,尤其是当我们具有不同单位的变量时。

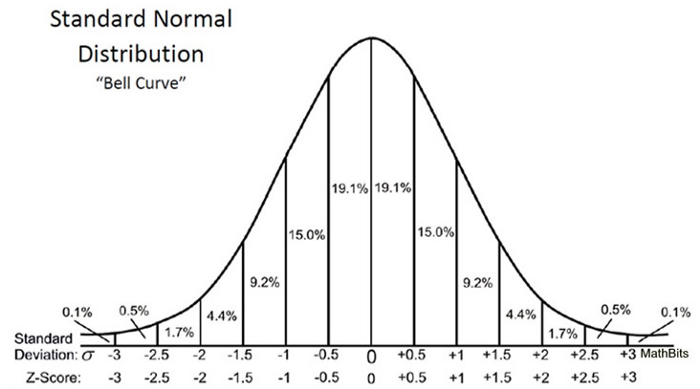
z得分可以告诉我们总体数据与平均人口数相比的位置。
我喜欢威尔森(Will Cursen)所说的:Z分数越高或越低,随机结果的可能性就越小,有意义的结果就越可能。
但是,多高(或低)被认为足以量化我们的结果有多重要?
高潮
在这里,我们需要最后一块解决难题,即p值,并根据我们在开始实验前设置的显着性水平(也称为alpha)来检查我们的结果是否具有统计学显着性。
3.什么是P值?
终于...我们在这里谈论p值!
前面所有的解释都是为了设置阶段并将我们引向该P值。我们需要前面的背景和步骤来理解这个神秘的(实际上不是那么神秘的)p值,以及它如何导致我们决定检验假设的p值。
如果您走了这么远,请继续阅读。因为本节是其中最激动人心的部分!
与其使用Wikipedia(对不起的Wikipedia)给出的定义解释p值,不如在我们的上下文中解释它-比萨送达时间!
提醒一下,我们随机选择了一些披萨递送时间,目的是检查递送时间是否超过30分钟。如果最终证据支持比萨店的要求(平均送达时间为30分钟或更短),那么我们将不会拒绝原假设。否则,我们驳斥原假设。
因此,p值的工作是回答以下问题:
如果我生活在一个比萨饼交货时间不超过30分钟(零假设是正确的)的世界中,那么我在现实生活中的证据有多意外?P值以数字(概率)回答这个问题。
p值越低,证据越出乎意料,我们的原假设就越荒谬。
当我们对原假设感到荒谬时,我们该怎么办?我们拒绝它并选择我们的替代假设。
如果p值低于给定的显着性水平(人们称其为alpha,我称其为荒谬的阈值-不要问为什么,对我来说更容易理解),那么我们将拒绝原假设。
现在我们了解了p值的含义。让我们将其应用于我们的案例中。
P值在计算披萨交付时间中
现在,我们已经收集了一些交货时间的样本数据,我们进行了计算,发现平均交货时间增加了10分钟,p值为0.03。
这意味着,在世界上披萨的发送时间为30分钟或更短(零假设是正确的)的世界中,由于随机噪声,我们有3%的机会看到平均发送时间至少长10分钟。 ...
p值越小,结果将越有意义,因为它不太可能由噪声引起。
在我们的情况下,大多数人会误解p值:
p值为0.03意味着有3%(概率百分比)的结果是偶然的-这是不正确的。人们经常想要一个确定的答案(包括我自己),这就是为什么我很久以来一直对p值的解释感到困惑。
p值不能证明任何东西。这只是将惊喜用作明智决策的基础的一种方法。我们可以使用以下方法使用p值0.03来帮助我们做出明智的决定(重要):
-卡西·科兹柯夫(Cassie Kozyrkov)
- 想象一下,我们生活在一个平均交货时间始终为30分钟或更短的世界中-因为我们相信比萨店(我们的原始信念)!
- 在分析收集到的样品的交付时间之后,p值比0.05的显着性水平低0.03(假设我们在实验之前设置了该值),并且可以说结果具有统计学意义。
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
到目前为止,您可能已经发现了一些问题...根据我们的上下文,p值尚未用于证明或证明任何事情。
我认为,当结果具有统计学意义时,p值用作挑战我们最初的信念(无效假设)的工具。当我们对自己的信念感到荒谬的时候(假设p值表示结果在统计上是有意义的),我们就放弃原始的信念(拒绝原假设)并做出明智的决定。
4.统计意义
最后,这是最后一步,我们将所有内容放在一起,并检查结果是否具有统计意义。
仅具有一个p值是不够的,我们需要设置一个阈值(重要性水平-alpha)。实验前应始终设置Alpha以避免偏差。如果观察到的p值小于alpha,则可以得出结论,该结果具有统计意义。
基本的经验法则是将alpha设置为0.05或0.01(同样,该值取决于您的任务)。
如前所述,假设我们在开始实验之前将alpha设置为0.05,由于p值0.03低于alpha,因此结果具有统计意义。
作为参考,以下是整个实验的主要步骤:
- 制定原假设
- 形成替代假设
- 确定要使用的Alpha值
- 查找与您的Alpha水平关联的Z得分
- 使用此公式查找测试统计信息
- 如果检验统计量小于Alpha Z分数(或p值小于Alpha值),则拒绝原假设。否则,请勿拒绝原假设。
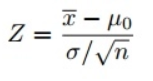
如果您想了解更多有关统计意义的信息,请随时阅读由Will Kersen撰写的这篇文章-解释统计意义。
随后的思考
这里有很多东西可以消化,不是吗?
我不能否认p值本质上使许多人感到困惑,而且我花了相当长的时间才能真正理解和欣赏p值以及它们如何在我们的决策过程中应用。作为数据科学家。
但不要过分依赖p值,因为它们仅在整个决策过程的一小部分起作用。
我希望我对p值的解释变得直观和有助于您理解p值的真正含义以及如何将其用于检验假设。
计算p值本身很简单。当我们想在假设检验中解释p值时,困难的部分就来了。希望现在困难的部分对您来说变得容易一些。
如果您想了解有关统计的更多信息,我强烈建议您阅读本书(目前正在阅读中!)- 《数据科学家实用统计》,专门为数据科学家撰写,以了解统计的基本概念。

通过参加SkillFactory的付费在线课程,了解如何从头开始或在技能和薪资水平上获得高水平职业的详细信息:
- 从头开始培训数据科学专业(12个月)
- 任意起点的分析师行业(9个月)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )