👋🏼 👨‍👩‍👧‍👧 ⏬ AES是美国的加密标准。第五部分攻击 👨‍👨‍👦 👂 🌂

周期中的其他文章

AES — . I

ES — . II

AES — . III

AES — . IV

AES — . V.

在详细介绍了各个变换的细节之后，使用了一个有限的，不是抽象的元素（如许多出版物中一样，不排除Khabrovsky），而是一个（具体的）代数领域，在其中实现了RIJNDAEL，AES-128和（执行AES-128标准的操作），我们可以继续考虑对密码的可能攻击。就目前而言，我们认为我们只能进行一次攻击，即最容易理解和最透明的哈伯攻击（尽管可能并非对所有读者而言）。

我已经习惯了缺点，但是魔鬼并没有开玩笑。许多作者已经对可能的攻击和预期结果进行了分析，但是，仅靠具体的成功例子或仅令人印象深刻的想法是远远不够的。在这里，我们将从数学的角度考虑使用入侵者引入密文的错误进行的攻击。在为示威选择攻击时，作者试图不让那些使用过分扭曲和深奥的数学知识的人参与进来，但所涉主题本身是相当严肃的，不允许继续对“手指”进行解释。

该出版物的一个重要目标是展示数学的应用，它构成了AES-128的基础，而且不幸的是，在很少有人能够检查和指出他们的发明这一事实的指导下，许多作者绕过或错误地解释了毫无根据和未经证实的事实。

本文的内容并不完全是攻击的原始概念，主要动作是从工作中采取的，但是我的学生精心设计，补充和测试了该攻击。他们在高等代数和密码学方面都有很好的实践。

1.攻击AES密码密钥

首先，在一个简单的案例中描述了对AES的攻击，然后很清楚如何概括这种攻击。所考虑攻击的目的是恢复密码的密钥K（Nr）。一旦确定了部分（回合）密钥K（Nr），就很容易获得密钥K。

1.1攻击原理

假设可以通过在操作ShiftRows（Nr-1）之后将错误“ε”引入状态矩阵S的单独字节（16个之一）中进行更改，即倒数第二轮，以及损坏字节（元素）的索引（单元号））状态。可以省略最后一个假设；引入该假设是为了更轻松地说明攻击机制。假定状态项的新值未知。

错误“ε”扩展到进程退出状态的不超过四个字节。对于输出状态的所有4个可变元素，在第1.4节中找到了可能误差为``ε''的向量的一组值（set）。另外，可以将这四个元素的可能值集``ε''（定义1）相交。当这样的集合相交时，可获得较小的集合，因此减少了进行完整分析所需的密文数量。

最后，对于每个错误，我们为上一个回合键的四个元素打印出一些可能的乱码。通过形成其他密文，我们找到了四个字节的回合密钥K（10）。即使对错误的位置有很多一般性的假设，这种攻击仍然可以成功。例如第9个MixColumns（）转换之前缺少有关错误位置的信息。带有和不带有失真的密文矩阵之间的差异将揭示失真及其位置（在示例中，这些位置分别为0、7、10、13）。

还假设在第8回合中引入的“ε”错误（在第8个MixColumns（）转换之前）可能对分析有用。但是同时，进行更完整分析所需的密文数量也增加了。对于所考虑的数字示例，在不考虑错误位置假设的条件下，需要大约十个密文才能获得四个字节的轮回密钥K（10）。

1.2错误对消息影响的数值示例

这里使用的示例与命名作品的附录中给出的相同。考虑了加密过程的倒数第二次和最后一轮（数据的字节表示形式为）：

输入= '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34';

密码密钥='2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C';

输出= '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32';

错误“ε” =“ 1E 00 00 00 00 00 00 00 00 00 00 00 00 00 00”。

下图显示了根据密码块长度和密码密钥长度每个16个字节（即Nb = 4和Nk = 4）在状态数组中包含的值。

错误传播以粗体和十六进制表示。以下是在不同情况下的国家广场：

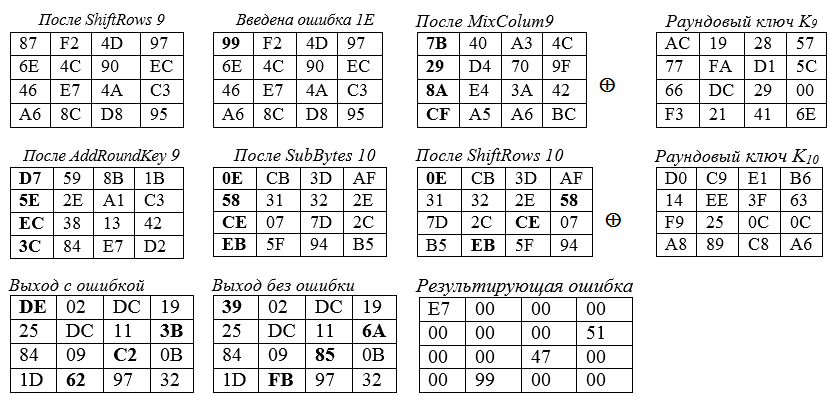
插入到第9个回合状态的第0个字节中的错误“ε” = 1E，导致最终状态的四个字节发生变化。状态“正方形”的主要对角线的角单元格的计算示例：

-将误差“ε” = 1E

87⊕1E = 10000111⊕0001 1110 = 1001 1001 = 99输入到第9个回合的状态正方形的左上（角）单元格

-右下将MixColum9之后的第9个圆角的状态与密钥字节K（9）相加：

BC⊕6E = 10111100⊕0110 1110 = 1101 0010 = d2。

-计算结果误差的值。

在存在两个消息文本的情况下（有无错误），通过从另一文本中减去一个文本来确定损坏的状态字节的值和位置。在我们的情况下，可以通过对两个文本求模而求和来代替这种减法。我们仅对于源文本中引入的错误更改的字节获得非零结果。

例如，以十六进制形式，我们可以找到误差值：

表7-计算误差值

结果，差值误差

ε_{0}^{'} = E 7, ε_{1}^{'} = 51, ε_{2}^{'} = 47, ε_{3}^{'} = 99

$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$ ... 让我们举一个计算最后一个错误字节的示例：

62⊕FB = 01100010⊕11111011= 1001 1001 =99。

状态字节的位置因错误而改变

ε_{0}^{'} = E 7, ε_{1}^{'} = 51, ε_{2}^{'} = 47, ε_{3}^{'} = 99

$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$ 。表示循环键（最后一轮）元素的索引，如K [0]，K [7]，K [10]，K [13]。此处，0、7、10、13是状态矩阵的单元号，矩阵Ao是用于混合加密过程各列的转换矩阵，其第一列的形式为：'02'，'01'，'01'，'03'。

注入的错误如何影响最终的最终状态

分析引入错误时获得的信息

可以包含有关密钥K（Nr）的信息的唯一操作是最后的SubBytes（）转换。因此，我们有四个方程，其中x0，x1，x2，x3，ε是未知变量。

我们想要获得以下四个方程的解：

s (x_{0} + 2 ε) + s (x_{0}) = ε_{0}^{'},

$s(x_0 +2ε) + s(x_0) =ε_0’,$

s (x_{1} + ε) + s (x_{1}) = ε_{1}^{'},

$s(x_1 +ε) + s(x_1) =ε_1’,$

s (x_{2} + ε) + s (x_{2}) = ε_{2}^{'},

$s(x_2 +ε) + s(x_2) =ε_2’,$

s (x_{3} + 3 ε) + s (x_{3}) = ε_{3}^{'},

$s(x_3 +3ε) + s(x_3) =ε_3’,$

字节数

ε_{0}^{'}, ε_{1}^{'}, ε_{2}^{'}, ε_{3}^{'}

$ε_0’, ε_1’, ε_2’, ε_3’$ 由错误修改的字段包含有关生成这些字节的未知密钥的信息。

所有这些方程式都可以归纳为一个方程式

s（x +cε）+ s（x）=ε'，（1）

其中常数= '01 '，'02'或'03'，我们将进一步求解该方程式，分析。

定义1。误差ε的等式（1）的解集由符号B（cε'）表示，并由以下表达式定义：

B（cε'）= S（cε'）= {εєGF [2 ⁸ ]：∃xєGF [2 ⁸ ]， s（x +cε）+ s（x）=ε'}，| B（cε'）| = 127。

这是与特定误差ε'相对应的单个误差区域。对于其他ε'，误差区域将不同。

定义2。考虑场GF（2）上的线性变换transformation：

ℓ：GF [2 ⁸ ]→GF [2 ⁸ ];

x→x ² + x。

ℓ的图像是Im（ℓ）GF（2）-向量空间的映射，即来自GF [2 ⁸ ]的元素集合

（x ² + x）表示1= Im（ℓ），其维数dimGF（2）（E1）= 7。 2 ⁸ ]方程x ² + x =θ，根据维埃塔定理，解满足关系x2 = x1 + 1和x2∙x1 =θ（模φx，（2 ⁸ -1））。变量θ是二次方程的一个自由项，下面以一个例子说明所考虑的线性变换。示例设置了GF字段[2 ⁸

]，则对其元素执行x→x ² + x转换。

表8-字段GF [2 ⁸ ]的初始片段以及元素转换的结果。

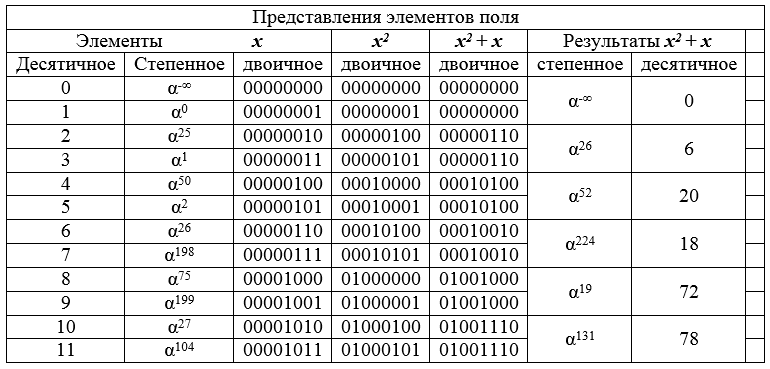
表8显示了转换如何将十进制顺序列表中的相邻对更改为相同的字段元素。由此可知，变换的结果（图像）比原图像小2倍（视场压缩了2倍）。集合尺寸收缩的这一原理构成了提出的攻击的基础。

命题2。对于λ1，λ2єGF [2 ⁸ ]-{0} ，以下陈述是正确的：

2.归纳与实施

首先，借助特殊的软件应用程序，将生成20个带有错误的密文。为此，将源文本，键，错误输入模型（程序），并设置放置错误的位置编号。通过按下“开始”按钮，程序将实施算法并以扩展形式显示有错误的文本，无错误的文本以及它们之间的差异的最后两轮加密的结果。此后，密文将正确无误地保存。错误值将周期性更改，并通过按“开始”按钮，将获得带有错误的下一个密文。在该列的一个值上形成了5个有错误的密文。

要实施攻击，您必须使用程序打开密文无误的文件，并使用程序打开有错误密文的文件（文件中的数据以十六进制形式显示），密文及其之间的差异显示为字节的方形数组（状态）。按下“搜索密钥”按钮，开始搜索密钥可能的字节的过程。进程的当前状态显示在文本框中。之后，打开带有另一个错误的密文，并重复该过程。收到第10轮密钥字节时，它也出现在相应的方形字节数组中。当运行前一阶段生成的所有20个密文有错误时，很有可能获得第10轮密钥的所有字节的值（否则，需要更多有错误的密文）。然后，根据给定的算法“使用最后一个子密钥恢复密码”来恢复加密密钥。在这里。

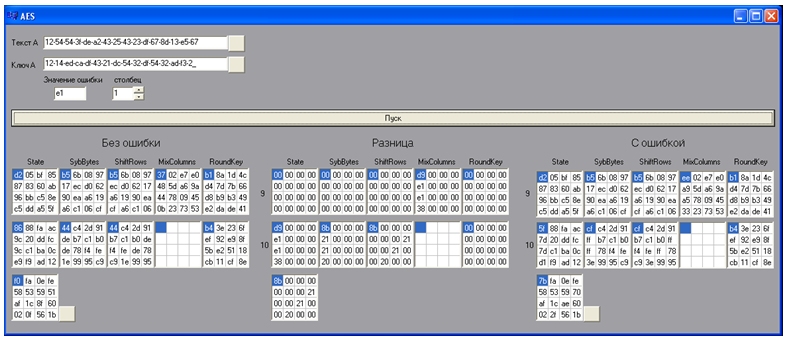
图11-用于构造带有错误的密文的软件产品

为了加快列举带有错误的密文的过程，可以在“查找键”按钮前打勾

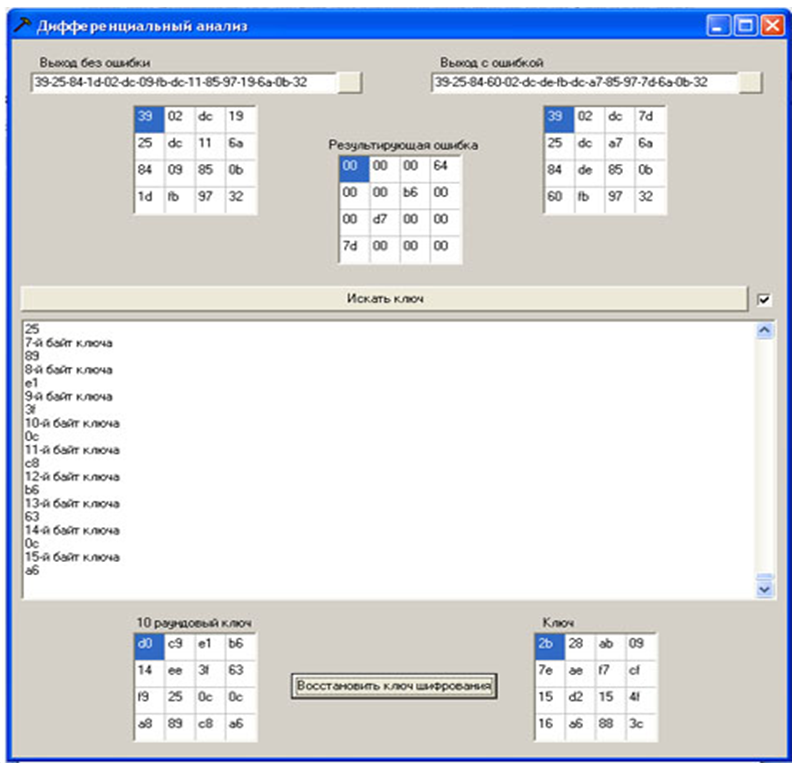
图12-攻击

的软件实现软件产品的示例：

源文本3243f6a8885a308d313198a2e0370734

密钥2b7e151628aed2a6abf7158809cf4f3c

错误1 1e000000000000000000000000000000

具有错误1的密文

可能的字节de25841d02bdc09

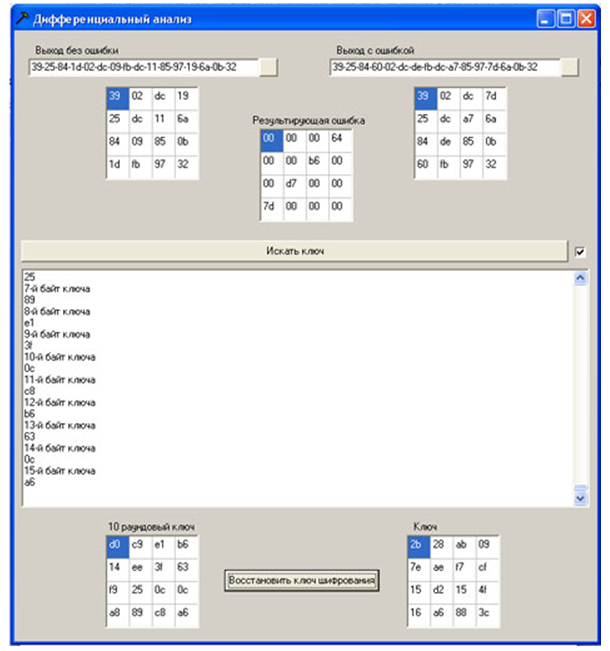
图13-程序操作示例

第10回合密钥d014f9a8c9ee2589e13f0cc8b6630ca6密钥已完全恢复

恢复的密钥2b7e151628aed2a6abf7158809cf4f3c与预期的匹配，与加密会话中指定的密钥相匹配。

2.1。没有错误位置信息的情况

此时，假定该错误包含在MixColumns操作的最后两次执行之间的状态字节中。除了可以将错误包含在1到16的字节之间之外，这是相同的情况。该错误乘以MixColumns操作并扩展到4个字节的状态。

在差分状态矩阵的第一行中会产生强制错误。通过查看强制错误列，可以确定输入的错误属于哪一列。这是通过使用前面的描述中所述的方法检查输入错误的四个可能的行位置来完成的。

2.2。硬件设备

假设您有能力在物理上干扰AES硬件设备。首先，让我们使用AES设备为十多个随机明文计算密码。然后，我们通过剪裁这些线并将它们连接到回合期间位于两个回合之前的两个字节之间的临时（临时）线上来修改示例项目。毕竟，我们在第Nk -2轮中有一个字节，总是用“ 00”（或“ FF”）代替。

我们再次计算与代理设备相同的消息。对于随机明文，有缺陷的字节就像一个随机错误。该单个错误转换为Nk -1轮中的四个错误和Nk轮中的十六个错误。在这种情况下，可以获得偏差矩阵（微分），借助于该矩阵，可以通过分析误差来找到最后一个回合密钥。

文献：

[1] FIPS PUB 197：高级加密标准，csrc.nist.gov/publications/fips/fips197/fips-197.pdf

[2] Boneh，DeMillo和Lipton，关于检查加密协议是否存在故障的重要性，《计算机科学讲义》，《密码学的进展》，《 EU-ROCRYPT'97的议事录》，第1页。 1997年第37-51页。

[3] E. Biham和A. Shamir，秘密密钥密码系统的差分故障分析，CS 0910，Crypto'97的论文集。

[4] Ross J. Anderson，Markus G. Kuhn：防篡改-警告说明，第二届USENIX电子商贸研讨会，加利福尼亚州奥克兰，1996年11月18-21日，第1-11页，ISBN 1-880446- 83-9。

AES是美国的加密标准。第五部分攻击