使用Python的贝叶斯网络-用示例解释
由于信息有限(尤其是俄语),贝叶斯网络周围存在许多问题。如果没有在那个时代的大多数先进技术中实现它们,人们就可以睡个好觉,例如人工智能和机器学习。
基于这个事实,本文完全致力于贝叶斯网络的工作以及它们本身如何无法形成问题,而是将其应用到它们的解决方案中,即使要解决的问题极为混乱。
文章结构
- 什么是贝叶斯网络?
- 什么是有向无环图?
- 贝叶斯网络中的数学原理
- 一个反映贝叶斯网络思想的例子
- 贝叶斯网络的本质
- Python中的贝叶斯网络
- 贝叶斯网络的应用
我们走吧。
什么是贝叶斯网络?
贝叶斯网络属于概率图形模型(GPM)的类别。VGM用于计算变异性,以用于概率概念。
贝叶斯网络的通用名称是Deep Networks。它们用于建模有向无环图。
什么是有向无环图?
有向无环图(像统计数据中的任何图一样)是节点和链接的结构,其中节点负责某些值,链接反映节点之间的关系。
非循环==没有定向循环。在图的上下文中,这种形容词表示从一个点开始的路径,我们不会遍历整个图,而只会遍历其中的一部分。 (例如,如果我们从图片中的节点2开始,则绝对不会到达节点1)。
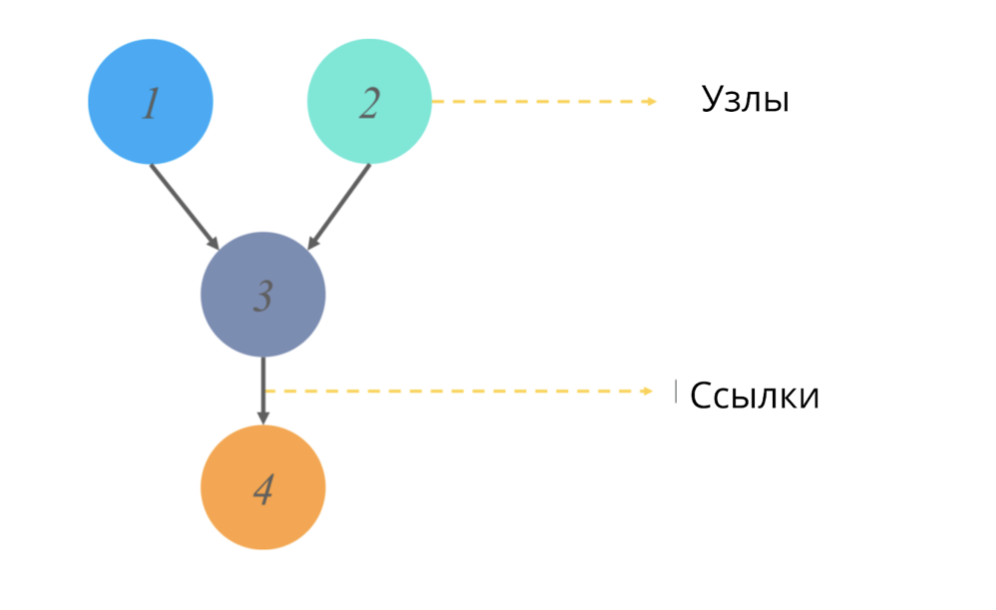
这些图模拟什么以及它们给出什么输出值?
不确定有向图的模型还基于每个随机值的事件概率起源的变化。条件概率表适用于表示和解释每个值,因此我们可以模拟顺序事件概率的分支。
一切都好。一开始我也很困惑。为了更好地理解,让我们分析贝叶斯网络的数学成分。
贝叶斯网络数学
正如定义中已经提到的那样,贝叶斯网络是基于概率理论的,因此,在开始使用贝叶斯网络之前,必须解决两个问题:
什么是条件概率?
联合平均概率分布是多少?
条件概率
某个X事件的条件概率是事件X发生的概率的数值,前提是已经发生了某些事件Y。
一个值的标准概率公式(本文中未给出):P(X)= n(x)/ N,其中n是要调查的事件,N是所有可能的事件。
对于两个值,适用以下公式:
如果X和Y是从属事件:
P(X或Y)= P(X⋂Y)/ P(Y),X和Y的概率的交集/概率Y上的概率。(分子中的符号“”表示概率的交集)
如果事件X和Y是独立的:
P(X或Y)= P(X),即研究中的事件彼此之间发生的可能性相同。
联合概率
联合概率是同时发生的两个或多个事件的统计度量的定义。也就是说,事件X,Y和C一起发生,我们使用值P(X⋂Y⋂C)反映事件的累积概率。
这在贝叶斯网络中如何工作?让我们来看一个例子。
反映贝叶斯网络本质的示例
假设我们需要对在考试中获得学生成绩之一的概率进行建模。
分数由以下组成:
- 考试难度等级(e):具有两个等级的离散变量(困难,容易)
- 学生智商:具有两个等级(低,高)的离散变量
所得的评估值将用作学生或女学生进入大学的可能性的预测因子(预测值)。
但是,IQ变量也会影响准入。
我们使用有向无环图和条件概率分布表表示所有值。
使用这种表示,我们可以计算一些累积概率,该累积概率由五个变量的条件概率的乘积形成。
累积概率:
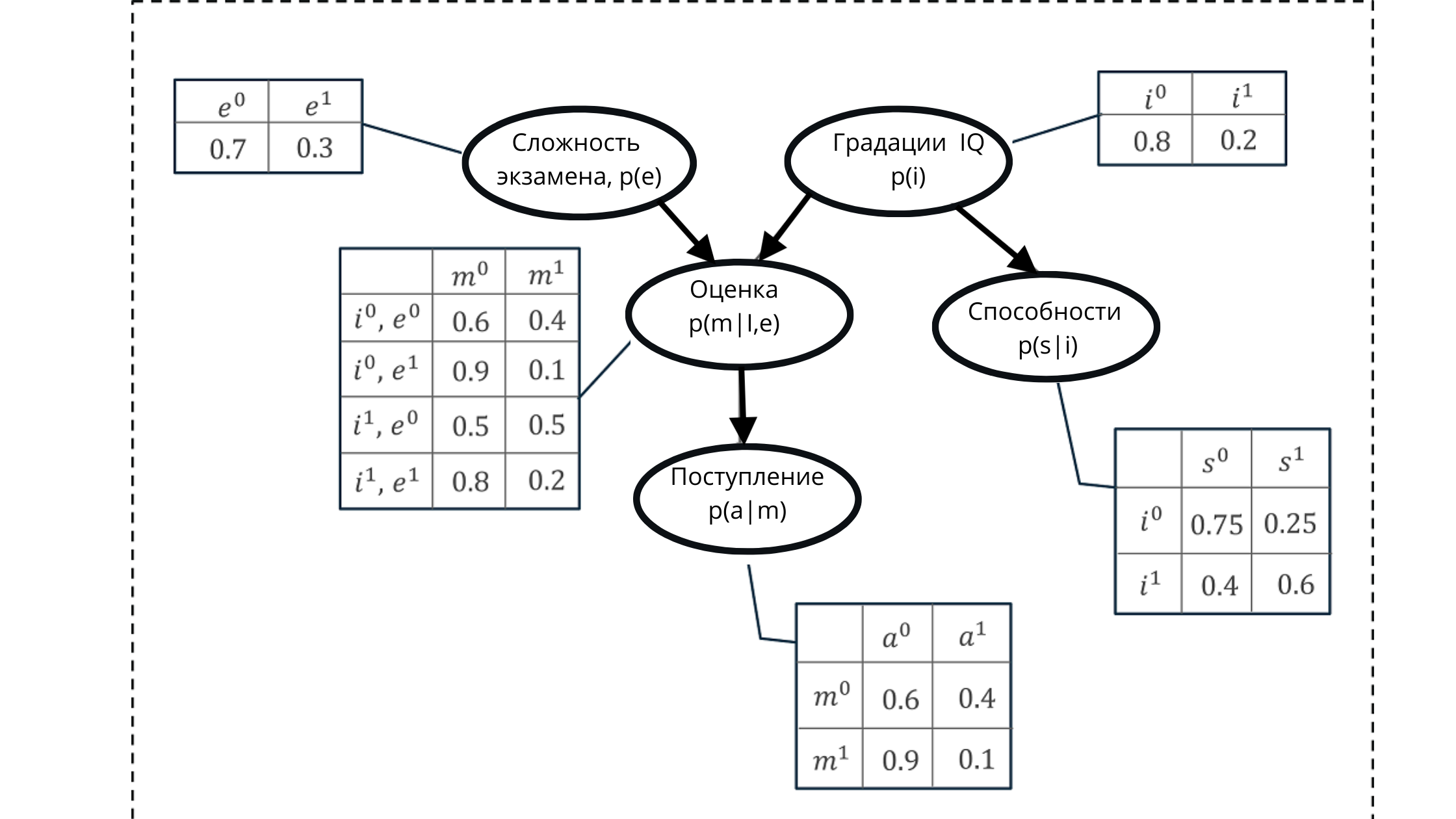
在图示中:
p(e)是检查变量等级的概率分布(影响等级p(m | i,e)))
p(i)是IQ变量等级的概率分布(影响等级p(m | i,e) )))
p(m | i,e)-基于智商水平和考试难度的年级概率分布(取决于p(i)和p(e))
p(s | i)-学生能力的概率系数,根据他的智商水平(取决于变量智商p(i)),
p(a | m)是学生对他的估计值p(m | i,e)的大学录取率。
在这里,我记得非周期图的性质是反映关系。在图中,我们可以清楚地看到父节点如何影响子节点以及子节点如何依赖父节点。
因此出现了使用贝叶斯网络生成的价值集的表述。
贝叶斯网络的本质
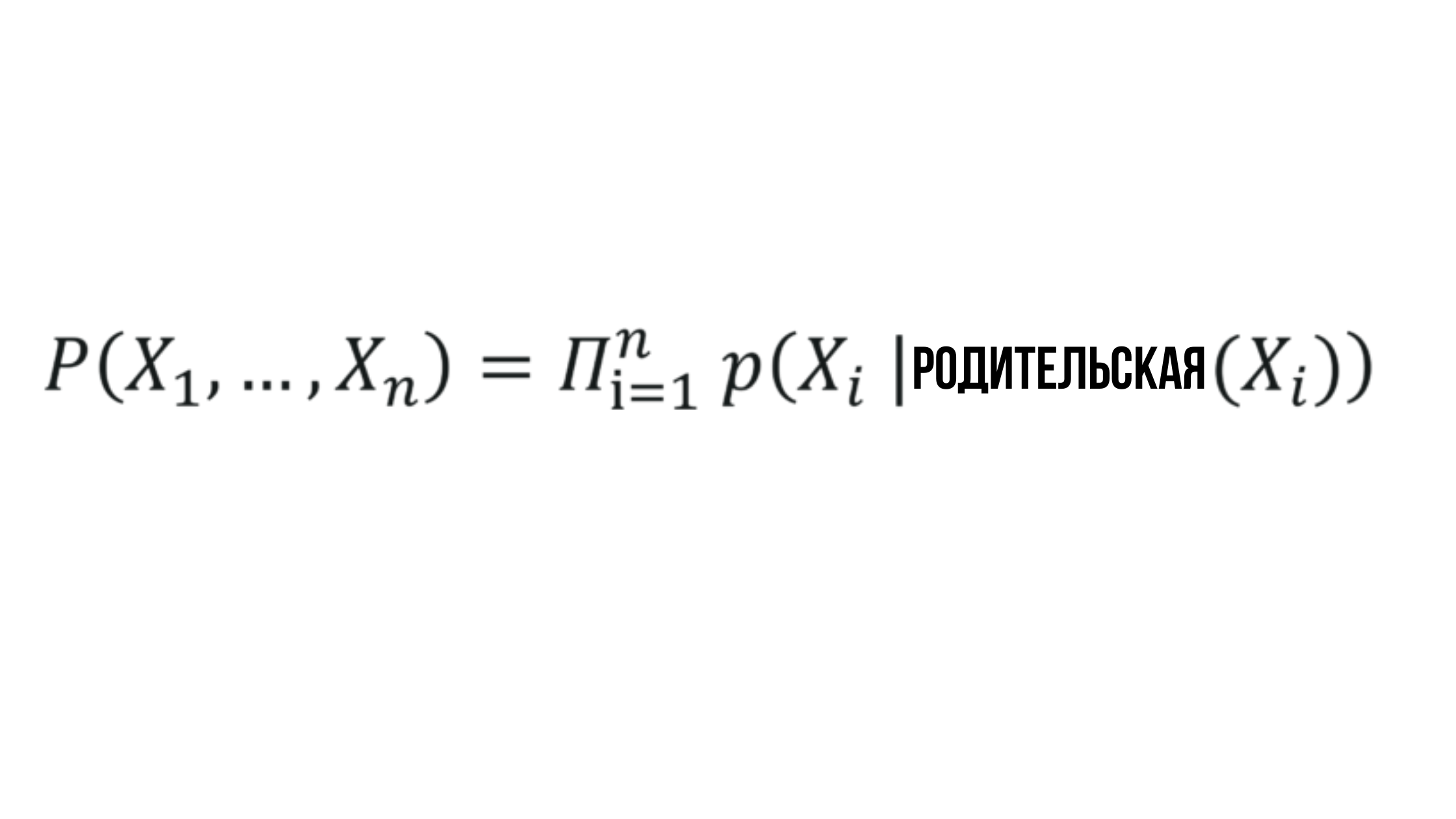
概率X_i取决于相应父节点的概率,并且可以由任何随机值表示。
听起来很简单,而且很正确-贝叶斯网络是描述性分析,预测建模等中使用的最简单方法之一。
Python中的贝叶斯网络
让我们看一下将贝叶斯网络应用于一个名为Monty Hall悖论的问题。
最重要的是:假设您是“奇迹之地”游戏更新格式的参与者。鼓不再旋转-现在您不应该应用F,而应按p进行演奏。
您面前有三扇门,一扇车也很可能位于后面。门后面没有汽车,将把您引向山羊。
选择之后,其余的领导者将打开通往山羊的那一个(例如,您选择了门1,这意味着领导者将打开门2或3)并邀请您更改选择。
问题:该怎么办?
解决方案:最初选择带有汽车的门的概率为33%,而选择山羊的门的概率为66%。
- 如果您命中了33%,换门将导致亏损=>获胜的机会== 33%
- 如果您击中66%,则更改将导致获胜=>获胜的概率== 66%
从数学逻辑的角度来看,总之改变门将导致百分之六十六的获胜,而导致百分之三十三的损失。因此,正确的策略是换门。
但是我们在这里谈论的是网络,可能会有很多门,所以我们将解决方案转移到模型中。
让我们构造一个包含三个节点的有向无环图:
- 奖门(总是有车)
- 可选门(带汽车或带山羊门)
- 在事件1中可打开的门(总是和山羊在一起)
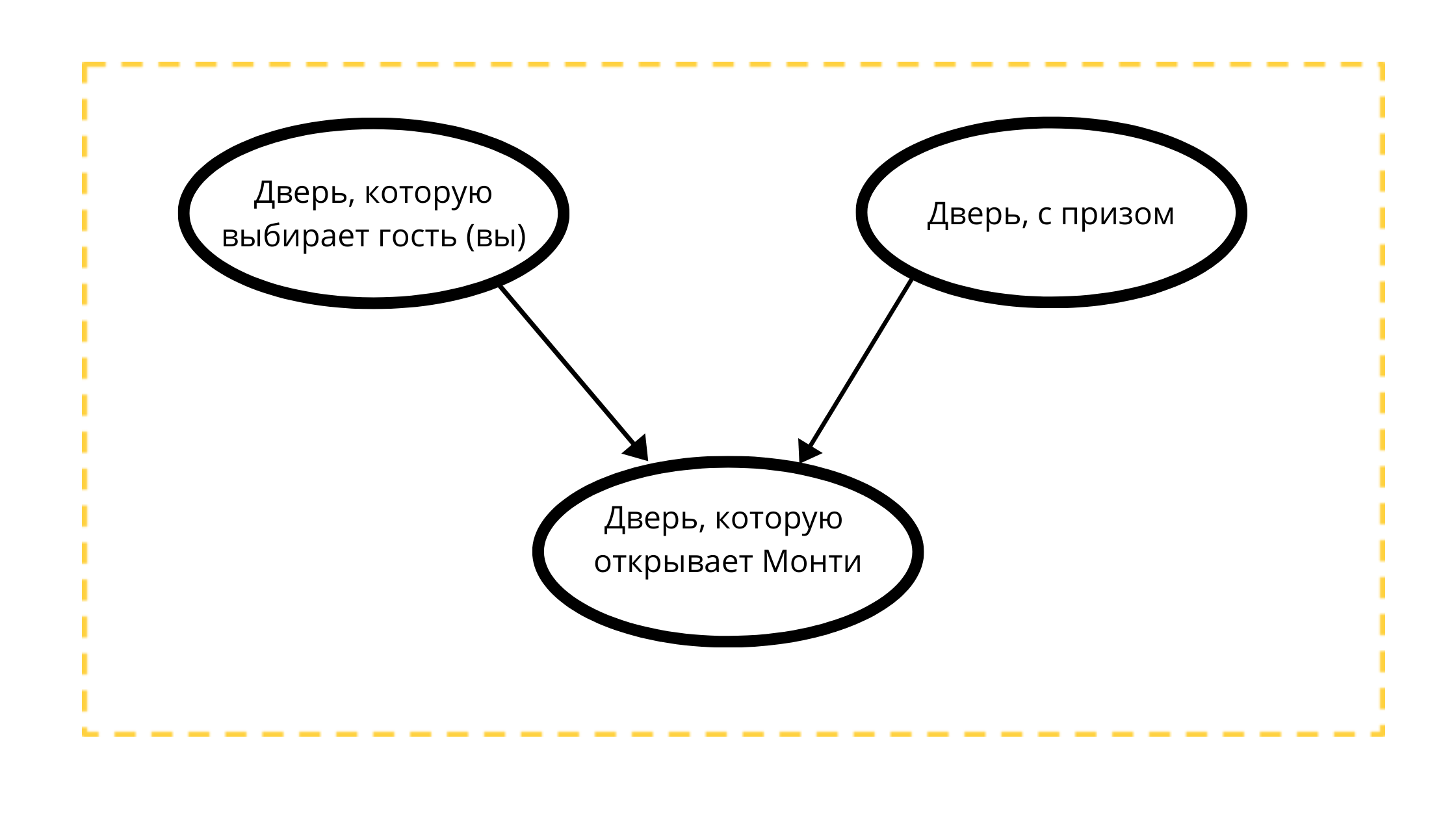
阅读计数:
Monty将打开的门严格受两个变量影响:
- 客人(您)蒙蒂100%选择的门不会打开您的选择
- 一扇有奖的门,也许蒙蒂总会打开一扇无奖的门。
根据经典示例的数学条件,奖品可以同等地位于任何一扇门的后面,就像您可以同等地选择任何一扇门一样。
#
import math
from pomegranate import *
# " " ( 3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# " " ( )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
# , ,
#
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
#
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()在摘要中的值是:
- A-客人选择的门
- B-奖门
- C-蒙蒂选择的门
在片段上,我们计算图的每个节点的概率值。在我们的示例中,顶部的两个节点服从相等的概率分布,而第三个节点则反映了从属分布。因此,为了不损失价值,对计算了游戏的每种可能组合的概率。
准备好数据后,我们创建了一个贝叶斯网络。
在此重要的是要注意,这种网络的特性之一是揭示隐藏变量对可观测变量的影响。同时,不需要预先指定或确定隐藏变量或可观察变量-模型本身会检查隐藏变量的影响,并且接收到的变量越多,精度越高。
让我们开始进行预测。
beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}让我们使用变量A的示例分析该片段。
假设来宾选择了该片段(A)。
在客人选择一扇门的阶段,“门后有奖品”事件的概率分布==⅓(因为每扇门都可能成为奖品)。
接下来,在蒙蒂选择门的阶段添加门概率值作为奖品。由于我们不知道步骤1中我们自己的(客人)选择是否排除了奖门,因此在此阶段该门成为奖品的概率为50/50
beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B
在这一步中,我们将修改网络的输入值。现在,它可以使用在步骤1和2中获得的概率分布,其中
- 我们选择获胜的机会没有改变(33%)
- 在蒙蒂(B)打开的门上赢得奖金的机会已被取消
- 被无人值守的机会成为门口奖品的机会占到了价值的66%
因此,如上所述,此游戏的客人正确的策略是更换门-数学上改变门的人有几率会赢得不改变门的人(⅓)。
在具有三个节点的示例中,手动计算无疑是足够的,但是随着变量,节点和影响因素的数量增加,贝叶斯网络能够解决预测值问题。
贝叶斯网络的应用
1.诊断:
- 基于症状的疾病预测
- 潜在疾病的症状建模
2.搜索互联网:
- 基于用户上下文(意图)的分析形成搜索结果
3.文件分类:
- 基于上下文分析的垃圾邮件过滤器
- 按类别/类别分配文件
4.基因工程
- 基于DNA片段的相互联系和关系对基因调控网络的行为进行建模
5.药品:
- 可接受剂量的监测和预测价值
上面的例子是事实。为了完全理解,有必要想象一下贝叶斯网络的创建在什么阶段被连接以及描述该图的图包括哪些节点。
蒙蒂·霍尔悖论的问题只是一个基础,它使人们可以“指尖”根据依赖和独立概率分布的组合来说明链的操作。我希望我明白了。
PS:我不是Python的王牌,只是学习,所以我不能对作者的代码负责。有关哈布雷的这篇文章的出版追求将更多的翻译知识作品推向世界。我认为将来我将能够生成自己的教程-在其中,我已经很高兴看到有关代码的建设性想法。