Clever Geek Handbook

关于VK数据的生日悖论

你好！



我决定使用VK提供的数据检查生日悖论。



什么是生日悖论？



尝试回答以下问题：一个房间中需要多少人才能使两个人有相同的生日（概率为0.5）？（日期和月份）。生日悖论回答了这个问题。



为了解决该问题，值得强调几个先决条件：



  1. 该模型将没有2月29日=>一年365天
  2. 365天中的每一天都是相同的可能性。


当然，生日的可能性是同样不完全现实的-有季节性的影响会影响孩子的出生日期，我想你自己可以猜出是哪个...



大多数人直觉地回答这个问题：180.看起来合乎逻辑，需要180个人才能拥有0.5个相同生日的概率（总共365天）。从未听说过生日悖论的每个人都与这种直觉有​​关。正确答案实际上远远小于180，甚至150，甚至100：23



。至少需要1个匹配的生日-因此我可以找到没有匹配的生日的可能性：

P(" ")=365∗364∗363∗...∗(365−k+1)365k=365!365k∗(365−k)!

...

这个想法是这样的：我选择第一个人并记住他的生日，然后第二个并计算他的生日与第一个人的生日不一致的概率；比第三个生日更远，我计算出他的生日与第一个和第二个生日不一致的概率。



求解方程式，结果表明需要23个人，生日重合的概率为0.5073，而100个人的生日概率为0.9999。



让我们看看VK数据的悖论吗？



从理论上讲，有23个人的生日一致概率为0.5073，有50个人的概率为0.97，有100个人的概率为0.99。让我们通过VK API进行检查。



1.我选择了VK中的一个大型社区。我决定参加Vkontakte上的MDK组。



首先，我用所需的列创建一个csv文件。 



with open('vk_data.csv', 'w') as new_file:
                # csv
                fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']

                csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')

                csv_writer.writeheader()

                newDict = dict()


我通过API登录到VK并设置了我需要的公众 

vk_session = vk_api.VkApi('username', 'password')
                vk_session.auth()

                vk = vk_session.get_api()
                
                vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')


我们开始解析VKontakte，他们的API仅允许您解析1000个用户，因此我创建了一个循环。 



for i in range(0, 20):
                    vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i,  fields = 'bdate')
                    for k in range(0, 1000):
                        try:
                            new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
                            new_file.write('\n')
                        except:
                            pass


从理论上讲，我们假设生日的可能性相同，但实际上会发生什么？我将建立一个生日直方图。



图片



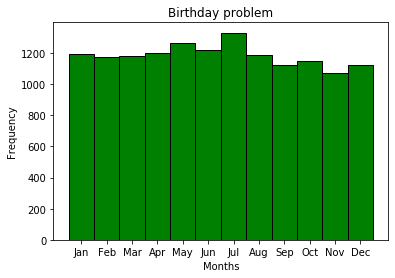
按月生日不是等概率的事件，通常这是很合乎逻辑的-这只是解决生日问题的先决条件。显然，在不同的位置会有不同的季节性事件。由于某些原因，7月是MDK订户生日最流行的月份。



我将凭经验估计一组50个人中至少有两个人生日相同的概率。为此，我编写了一个循环，在此循环中，表格中出现了50行的子样本。对于条件内的这50条线，我检查了生日匹配。如果匹配，那么我会在计数器变量中记住它，随后我将其除以周期长度以获得概率。 



fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
    fifty = df["dandm"].sample(n = 50)
    for j in fifty.duplicated():
        if j == True:
            counter = counter + 1
            break
print(':', counter / 1000)


获得的概率在0.97左右，与理论数据一致。



输出量



观察理论与经验主义之间的关系很有趣，在这种情况下，数据证实了理论。应该注意的是，该结果具有代表性，因为样本足够大-20,000人。



资源资源



  1. 哈佛大学。生日问题，概率属性| 统计信息110。URL：www.youtube.com/watch?v=LZ5Wergp_PA&t=150s。访问时间：2020年7月8日
  2. 生日问题。网址：en.wikipedia.org/wiki/Birthday_problem。访问时间：2020年7月8日>


More articles:


All Articles