
Armored Warfare:Armata项目是由Myods游戏工作室Allods Team开发的免费在线坦克动作游戏。尽管游戏是在CryEngine上制作的,CryEngine是一种非常流行的具有良好实时渲染的引擎,但是对于我们的游戏,我们必须从头开始进行修改和创建很多东西。在本文中,我想谈谈我们如何为第一人称视角实现色差,以及它是什么。
什么是色差?
色差是一种镜片缺陷,其中并非所有颜色都到达同一点。这是由于以下事实:介质的折射率取决于光的波长(请参见色散)。例如,当镜头没有色差时,情况就是这样:
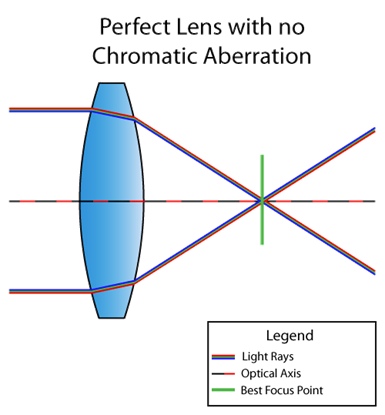
这是一个有缺陷的镜头:
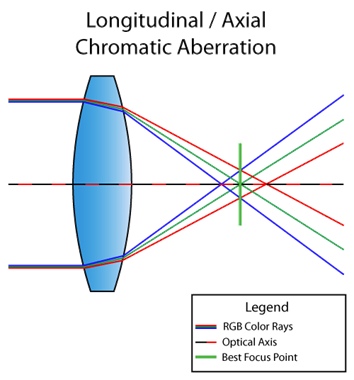
顺便说一句,上述情况称为纵向(或轴向)色差。当不同的波长穿过镜头后没有在焦平面的同一点会聚时,就会发生这种情况。然后,缺陷在整个图片中可见:

在上图中,您可以看到紫色和绿色由于缺陷而脱颖而出。看不到?在这张照片中?

还存在横向(或横向)色差。当光线以一定角度入射到镜头时会发生这种情况。结果,不同波长的光会聚在焦平面的不同点上。这是供您理解的图片:
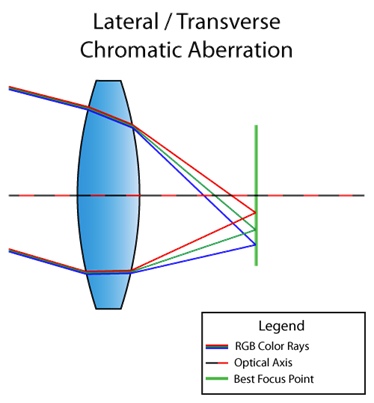
从图中您已经可以看到,结果是我们将光从红色完全分解为紫色。与纵向不同,横向色差永远不会出现在中心,而只会靠近图像的边缘。为了让您理解我的意思,这是互联网上的另一张照片:

好吧,既然我们已经完成了理论工作,那么让我们开始吧。
横向色差与光分解
首先,我将回答许多人的脑海中可能出现的问题:“ CryEngine是否实现了色差?” 有。但是它在具有锐化功能的同一着色器中的后期处理阶段使用,并且算法如下所示(链接至代码):
screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;原则上可行。但是我们有一个关于坦克的游戏。我们仅在第一人称视角时需要这种效果,而在美时才需要这种效果,也就是说,一切都聚焦在中心(您好为横向像差)。因此,当前的实现至少不适合于其效果在整个图片中可见的事实。
这是像差本身的外观(注意左侧):

这是扭曲参数时的外观:

因此,我们将目标设定为:
- 实施横向色差,以便使所有焦点都集中在示波器附近,如果侧面看不到特征色缺陷,则至少要模糊。
- 通过将RGB通道乘以对应于特定波长的系数来对纹理进行采样。我还没有谈论过这一点,所以现在可能还不清楚。但是,我们稍后一定会考虑所有细节。
首先,让我们看一下创建横向色差的一般机制和代码。
half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;
因此,首先构建一个圆形蒙版,该蒙版负责到屏幕中心的距离,然后计算到屏幕中心的方向,然后将所有这些乘以
blur。Blur和falloff-这些都是从外面通过,只是乘数调整像差参数。此外,还会从外部抛出一个参数,该参数sampleCount不仅负责采样数,而且实际上还负责采样点之间的步长,因为
half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);
现在我们只需
sampleCount要从纹理的给定点走一次,每次移动offsetDecrement,将通道乘以相应的波长权重,然后除以这些权重之和即可。好了,该谈论我们全球目标的第二点了。
可见光谱范围为380 nm(紫)至780 nm(红)。而且,可以将波长转换为RGB调色板。在Python中,执行此操作的代码如下所示:
def get_color(waveLength):
if waveLength >= 380 and waveLength < 440:
red = -(waveLength - 440.0) / (440.0 - 380.0)
green = 0.0
blue = 1.0
elif waveLength >= 440 and waveLength < 490:
red = 0.0
green = (waveLength - 440.0) / (490.0 - 440.0)
blue = 1.0
elif waveLength >= 490 and waveLength < 510:
red = 0.0
green = 1.0
blue = -(waveLength - 510.0) / (510.0 - 490.0)
elif waveLength >= 510 and waveLength < 580:
red = (waveLength - 510.0) / (580.0 - 510.0)
green = 1.0
blue = 0.0
elif waveLength >= 580 and waveLength < 645:
red = 1.0
green = -(waveLength - 645.0) / (645.0 - 580.0)
blue = 0.0
elif waveLength >= 645 and waveLength < 781:
red = 1.0
green = 0.0
blue = 0.0
else:
red = 0.0
green = 0.0
blue = 0.0
factor = 0.0
if waveLength >= 380 and waveLength < 420:
factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
elif waveLength >= 420 and waveLength < 701:
factor = 1.0
elif waveLength >= 701 and waveLength < 781:
factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
gamma = 0.80
R = (red * factor)**gamma if red > 0 else 0
G = (green * factor)**gamma if green > 0 else 0
B = (blue * factor)**gamma if blue > 0 else 0
return R, G, B
结果,我们得到以下颜色分布:

简而言之,该图显示了特定长度的波中包含多少颜色。在纵坐标轴上,我们得到的权重与我之前提到的相同。现在,我们可以完全实现算法,同时考虑到前面所述的内容:
half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
for (int i = 0; i < sampleCount; i++)
{
waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
Weight.r = GetRedWeight(waveLength);
Weight.g = GetGreenWeight(waveLength);
Weight.b = GetBlueWeight(waveLength);
offset -= offsetDecrement;
color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
accumulator.rgb += color.rgb * Weight.rgb;
WeightSum.rgb += Weight.rgb;
}
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);
也就是说,我们的想法是,我们拥有的越多
sampleCount,采样点之间的步距就越少,并且我们散射的光就越多(我们考虑了更多不同长度的波)。
如果还不清楚,那么让我们来看看一个具体的例子,即我们的第一次尝试,我将解释什么承担
startWaveLength和endWaveLength,和中的功能将如何实现GetRed(Green, Blue)Weight。
拟合整个可见光谱
因此,从上面的图表中,我们知道每个波长的RGB调色板的近似比率和近似值。例如,对于380 nm(紫色)的波长(请参见同一图),我们看到的是RGB(0.4、0、0.4)。这些是我们先前所说的权重所采用的价值观。
现在,让我们尝试摆脱通过四次多项式获得颜色的功能,以使计算更便宜(我们不是皮克斯工作室,而是游戏工作室:计算越便宜越好)。该四次多项式应近似结果图。为了构建多项式,我使用了SciPy库:
wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)
结果,获得以下结果(我将其划分为3个与每个单独的通道相对应的单独的图形,以便更轻松地与确切值进行比较):
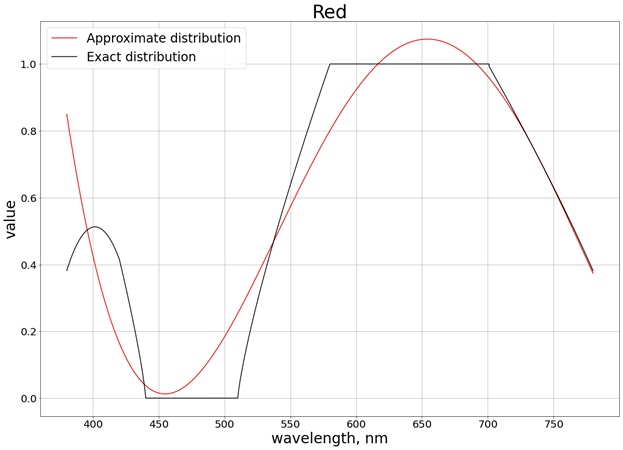
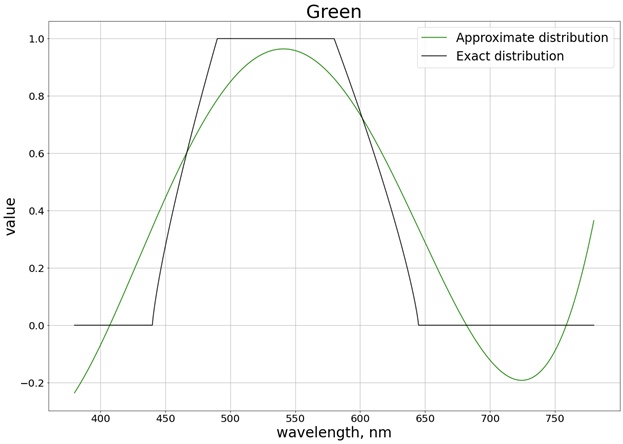
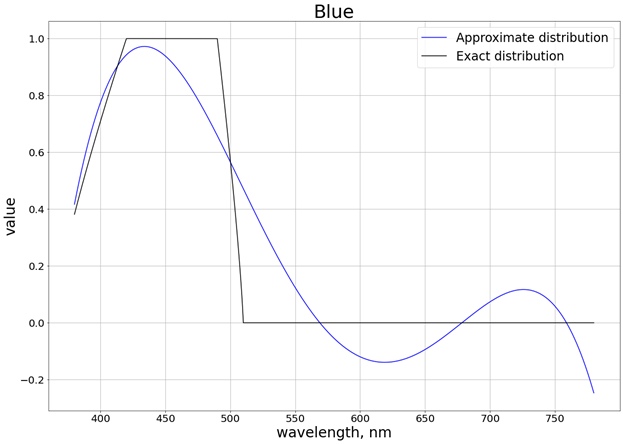
为了确保值不超过段[0,1]的限制,我们使用函数
saturate。例如,对于红色,获得函数:
half GetRedWeight(half x)
{
return saturate(0.8004883122689207 +
1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) -
1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}
缺少的参数
startWaveLength,endWaveLength在这种情况下分别为780 nm和380 nm。实际上,结果sampleCount=3如下所示(请参见图片的边缘):

如果我们调整值,将其
sampleCount增加到400,那么一切都会变得更好:

不幸的是,我们有一个实时渲染,其中一个着色器中不允许有400个样本(大约3-4个)。因此,我们稍微减小了波长范围。
可见光谱的一部分
让我们取一个范围,以便最终得到纯红色和纯蓝色。我们还拒绝左侧的红色尾巴,因为它极大地影响了最终多项式。结果,我们得到了段[440,670]上的分布:

另外,由于现在我们只能为值更改的段获取多项式,因此无需在整个段上进行插值。例如,对于红色,这是段[510,580],其中权重值从0到1变化。在这种情况下,您可以获得二阶多项式,然后
saturate该函数也将其减小到值[0,1]的范围。对于所有三种颜色,我们得到以下结果并考虑了饱和度:

结果,我们得到例如红色的以下多项式:
half GetRedWeight(half x)
{
return saturate(0.5764348105166407 +
0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) -
0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}
并在实践中
sampleCount=3:

在这种情况下,通过扭曲设置,可以获得与在可见光谱的整个范围内采样时大致相同的结果:

因此,使用二阶多项式,我们在440 nm至670 nm的波长范围内获得了良好的结果。
优化
除了通过多项式优化计算之外,您还可以优化着色器的工作,这取决于我们在横向色差基础上建立的机制,即,不要在总位移不超过当前像素的区域中进行计算,否则我们将对其进行采样像素,我们得到它。
看起来像这样:
bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
return OUT;
}
优化很小,但是非常值得骄傲。
结论
横向色差本身看起来很酷;此缺陷不会干扰中央的视线。将光分解为重量的想法是一个非常有趣的实验,如果您的引擎或游戏允许三个以上的样本,则可以给出完全不同的图像。在我们的案例中,可能不会费心并提出不同的算法,因为即使进行了优化,我们也无法负担很多样本,例如,3个样本与5个样本之间的差异不是很明显。您可以自己尝试上述方法并查看结果。