现象的数学模型假定所有过程都发生在4维时空中，其中SRT现象来自坐标系旋转转换过程中事件间隔的保留。不可否认的是，现实一直延伸到数学构造上。此外，实际上难以想象的虚数在其中发挥几乎完全重要的作用这一事实并不会削弱科学的成功。甚至E. Mach都说，如果用公式很好地描述观察到的现象，那么解释也是多余的。而且，我们不要与这种经验批评争论。
数学家发明了抽象并将其应用于现实。因此，奇点，虫洞和其他奇特的东西。也许值得幻想一下，例如，如果洛伦兹收缩的原因是一些假设的物理机制，那么我们对世界的看法将会发生什么变化。为什么不？
1洛伦兹收缩的物理原因
首先，我将表达看似显而易见的格言，即粒子，原子，分子通过物理场彼此相互作用。我们当然可以说它们交换了量子粒子，但是我们现在正在相对论理论领域，所以现在我们将忘记量子。因此，第一个奇妙的假设是，正是由于场效应的相互平衡，才将粒子添加到特定的构造和形体中。如果某些粒子偏离平衡位置，则将产生磁场干扰，这将使其余粒子移动，进而将导致它们对这个粒子产生反向场效应。
而第二个假设是，场扰动以一定的速度在一定的公共空间内传播。这个假设的奇妙性质是，根据科学，该场本身存在于4维时空（P-W）中，不会散布在任何东西上。总的来说，这在科学上是困难的。我们将假设这些场在一个单一的3维空间中扩散并存在-我们就是地球和恒星。似乎这不用说，谁也不知道，但让我们看看会发生什么。那些对公式不感兴趣的人可以将自己限制为仅阅读所选文本。
因此，我们同意粒子之间存在相互作用时间，这是由他们对他们的愤慨到达的时间和他们的回应返回的时间组成的。结果，身体的先前构造将逐渐恢复。图1决定粒子位置的场影响
对于人体的任何一点，都可以区分点组，这些点将具有相等的交互作用时间，并且我们将其称为等时点。情况反映在图1中。自然地，在静止时，围绕一个点的任何静止半径R的球都是与其等时的点的轨迹（GMT）。
请注意，粒子在每个时刻的运动由与之等时的所有粒子组的总数同时施加的合力的总和决定...让我们尝试找出由GMT的表面（由一组点2、3等组成）在人体移动时将如何变化。与点1的交互时间相同，该点可能不再是球体。
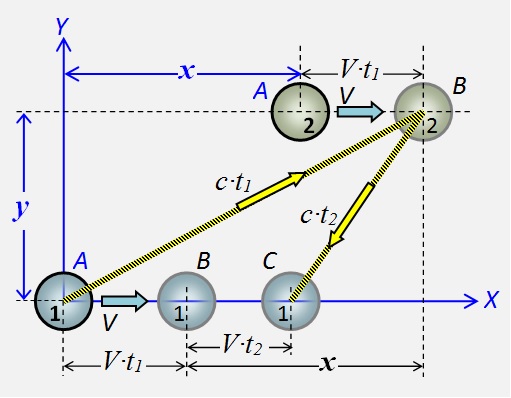让身体点1和2相互固定并以速度V同步地向右移动。当原点为一个点时，扰动场将发送到点2。标有字母A的点的相互排列 。图2人体前后点的场相互作用示意图
当扰动到达点2时，其传播距离为V∙t 1。用字母B标记点的位置。在扰动从点2返回到点1的时间内，点2将覆盖距离V∙t 2。他们的新职位以C标记。
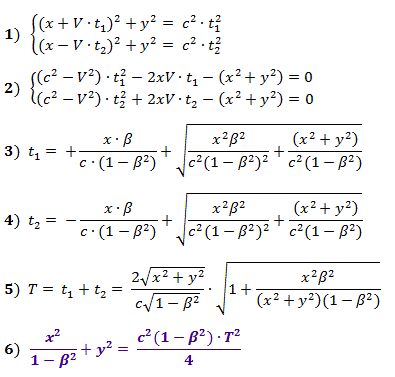根据毕达哥拉斯定理，公式（1）描述了图2中的距离，从中获得的距离（2）是用于计算时间t 1和t 2的方程式，其值由公式（3）和（4）给出根的正值，其中β = V / c。
公式（5）给出了从发送干扰到接收响应的交互时间值。
从等式（5）中，我们得到等式（1）的相互作用时间相同的等时点几何位置的坐标x和y的等式（6）。
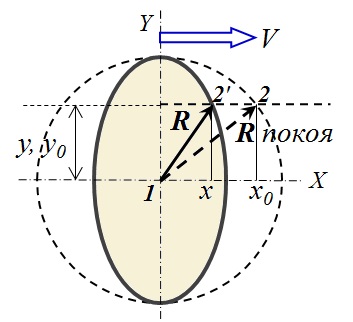式（6）描述了由图3中所示的椭圆形，沿着运动方向上被压缩（沿X轴）。√（1 - β 2）倍，即，按Lorentz的公式。静止时，球体表面上的点 2将移动到位置2'。在这种情况下，与静止点1等时的物质点在移动过程中将保持与它等时。图3
因此，在移动时，精确地根据Lorentz压缩了实物，因为物理场的“图片”被压缩了，从而确保了其空间完整性。
由于围绕对象每个点的所有等时点的洛伦兹收缩都相同，因此整个运动对象将沿运动轴成比例地收缩。
2.时间膨胀公式的推导
让我们确定与静止时的交互时间相比，对象移动时的交互时间。
公式（7）根据
等式（6）将点在移动过程中的坐标与静止时的坐标关联起来。公式（8）计算静止时的相互作用时间。公式（9）和（10）由公式（6）通过将公式（7）的坐标x和y以及其余部分的 R的值代入其中而获得。公式（11）等于（10）。通过将公式（8）的左侧代入公式（12），可以从公式（12）中获得公式（12），该公式将静态和运动期间的相互作用时间联系起来。在传统形式中，这反映在公式（13）中，其中T 0是静止物体中事件之间的时间间隔，而T是运动物体中相同事件之间的时间间隔。
因此，与静止时的交互时间相比，根据洛伦兹，运动对象中所有点的交互时间以相同的比例增加。因此，通常，移动物体中的所有过程实际上都在相同方面减慢速度。
如果我们考虑到相互作用粒子后方的场干扰必须在运动方向上赶上前者，那么时间变慢的原因很容易理解。当身体的速度几乎等于光速时，将需要很长时间才能赶上，如果身体的速度等于光速，则它将永远不会追赶。身体上所有的变化都会停止，而时间似乎会停止。
3，解释光速恒定等现象
让我们做一个思想实验。让一列光从火车的最后一辆车发出，这是在火车的头车中接收的。我们必须测量光在其自身系统中的长度为L 0的火车通过时所花费的时间T 0。在证明中，我们将使用有关空间均匀性和各向同性的假设，特别是，我们将假设火车的前半部分和后半部分以及向前和向后方向的测量结果相同。但是，严格来说，这些假设仅在实验的位置和时间内有效。图4。通过思想实验确定行进中的火车的光速
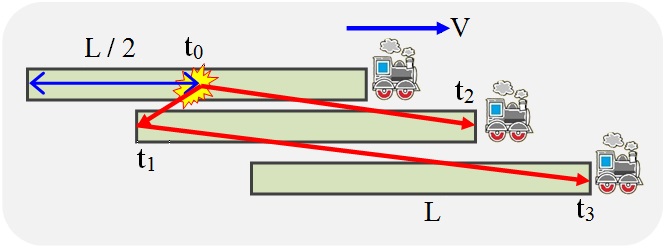
为了使从火车的最后一辆车发出信号的时刻与在其前车厢中的计时器的开始时刻同步，我们使用从火车中间到两端的光的起始脉冲。
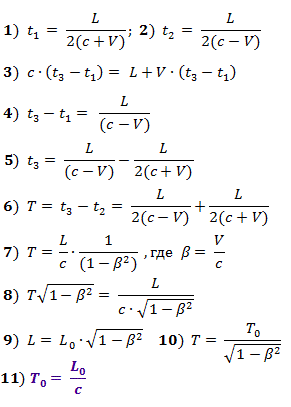
当来自火车中央的启动信号到达其尾巴（时间 t 1）时，将发送一个光脉冲。当开始信号到达火车头时（时间 t 2），倒数开始，直到发送的脉冲到达。
当光到达尾巴时，其速度加到火车的速度上；当光到达头尾时，减去火车的速度。我们获得以下公式（1）-（6）中给出的关系。
时间T = t 3 -t 2是时间间隔，根据火车上的观察者，它将火车信号从发车结束的那一刻（从那里接收到开始信号的那一刻）到接收到火车头的那一刻的事件分开。
从（6）得到公式（7），然后将其转换为形式（8）。此外，我们将考虑到这里所有的量L，T和t都是在进行思想实验的空间中的外部观察者的参考系中测量的。但是，当物体在空间中移动时，其长度（如第1章所述）实际上经历了洛伦兹收缩，而事件的次数如第2章所示，实际上减慢了相同的次数，即进行的时间比休息的时间长，这反映在公式（9）和（10）中。将这些比率代入公式（8）中，得出间隔T-光从火车尾部到火车头的传播时间，得出关系式（11）。
但是，对于相同事件，这些T 0和L 0与静止时的时间和长度有什么关系，以与行驶中的火车相关的惯性参考系（IRF）来衡量？显然，他们是平等的。事实是，时间和长度是通过与标准的关系用数字表示的。因此，静止时某物的时间和空间坐标的测量将在数值上进行等于在移动的ISO中进行的测量，因为移动时测量和标准的值都会成比例地变化。
问题是它们在太空中移动时究竟有多精确地变化。火车的思想实验证明，它们的变化方式使IFR中测量的光速数值保持等于其在太空中的速度值。这恰恰不是先验的明显证据和必需的证明。
我们看到“光速恒定的假设”是仅从洛伦兹收缩这一事实得出的，这在数学上是从物质位置对空间中物理场的传播速度和构型的依赖性得出的。
为了使图片更完整，我们还定义了整个火车运动的光速，例如，车厢壁之间的距离为S 0。为此，我们测量来回移动光脉冲（2·t 0）的时间。鉴于“那里”和“后面”的明显对称性，我们将仅考虑“那里”。在外部观察者的系统中，空间运动如图5所示。
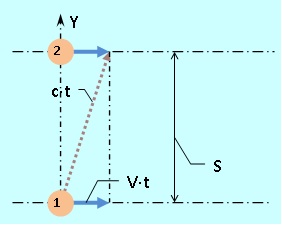因此，我们有（c·t）2 = S 2 +（V·t）2，由此我们得到t = S /（c·√（1-β²）），其中β= V / c。
在火车系统中，经过的适当时间t 0通过时间关系t = t 0 /（√（1-β²））与空间中经过的时间有关。将该表达式代入空间中t的公式中，得到t 0 = S / c。
图5。通过思想实验来确定行进中的火车的光速/
在相同t 0的火车自身系统中，我们具有关系t 0 = S 0 / c 0。但是由于横向尺寸在移动过程中不会改变，即S = S 0，得到c 0 = c。
我想没有必要证明光束任意方向上测得的光速的恒定性，这只会增加不必要的复杂性。考虑到已证明的光速不变性，很容易得出洛伦兹变换（L），并且对麦克斯韦方程或数学上抽象的Minkowski空间没有任何吸引力。
4.洛伦兹变换的推导
事件包括光脉冲到达参考系统{X'，Y'}中位于不变坐标x'和y'的点“ E ”处，相对于固定IFR {X，Y} 以速度V移动，两个CO的点O和O'重合。图6。在以CO {X，Y}为单位的自己的CO {X'，Y'}长度L中，x'坐标将对应。对于该事件，方程式（1）的系统是有效的，求解后我们可以得到（2），然后得到（3）和（4）。 由于运动物体的长度是根据洛伦兹压缩的，因此，如第3章中所述，光速在任何FR中都是相同的，因此对于适当的x'和
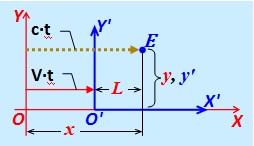
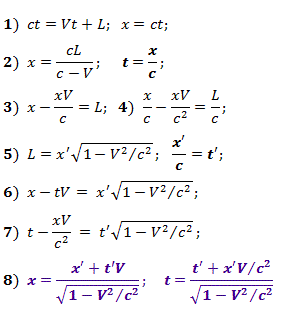
{X'，Y'}关系（5）中的 t'有效。将关系从（5）代入（3），我们得到（6），然后将它们代入（4），我们得到（7）。借助于运动的相对性，我们可以考虑运动系统{X，Y}，但是在（6）和（7）中，有必要用阴影部分替换未阴影的变量，并且速度 V应该取相反的符号，或者简单地针对 x和 t求解系统。
结果，我们获得了不同IFR中事件的坐标和时间的Lorentz变换的规范形式的表达式（8）。
当使用PL作为纯粹的形式化数学方法时，SRT现象的物理机制仍然不清楚。因此，在我以前的有关相对论多普勒效应和原则上，没有使用光像差以及移动倾斜镜的反射定律来证明这些现象的物理原因。
5.相对论的合理性及其适用性的限制
注意，如果在图1的图表中处于静止状态，则从点1到与它等时的点的GMT的干扰是同时发生的，则在运动过程中，在图2的图表中，这种干扰不再得到满足。在此GMT的每个点，将在不同时间创建对干扰的响应，但它们将同时在点1收敛。问题是，结果将与休息时一样吗？
上面已经证明，在任何IFR中，测得的正确时间和所有点之间的距离将与静止时相同。因此，例如启动的周期数任何一点之间的电磁波将与静止时相同。由于可以通过一系列单色谐波的扩展来表示任意配置的场的扰动，因此本征系统中所有场的配置和强度在静止时将分别相同。因此，不会违反构成主体的场的相位关系和同步，并且其中的所有过程都将像在休息期间一样进行。
这正是爱因斯坦的“相对论”所宣称的，并且正如我们所看到的，它在数学上是不可避免地从两个假设推论出来的（请参阅第1章），让我提醒您：第一：真实粒子的位置由场的结构决定，第二，场传播以有限的速度发生。
也就是说，相对性原则已经不是先验的普遍原则，而是结果，并且具有明显的适用范围。特别地，光速不具有世界常数的含义，而是在空间的特定区域中光的特定速度。在某些地方，由于与局部物理场（例如重力）的相互作用，它可能有所不同。因此，我们有两种选择可以得出完全相同的相对论公式：
- 首先，是正统的和科学的：它要求假设相对论的先验真实原理；
- : ,
在第一种情况下， SRT现象无需解释，其原因和机制仍然未知。问题“为什么？” 它甚至超出了科学范围。
在第二个假设中，这些假设甚至是很合逻辑的，不需要假设，并且仅在科学中接受相对主义的其他原因的情况下，它们才是“奇妙的”。对于“为什么这样的SRT现象如此？”的问题 这里给出了一个清晰的甚至几乎是微不足道的解释。但是迫切需要找出物质的性质以及它与物理场之间的关系。
因此，我们将继续幻想。
6.推导公式E =Mc²和动力学方程
首先，让我们找出相对论速度下的力是如何变化的。让我们选择体内平衡力作用于其上的体积元素。当身体移动时，所选元素的纵向尺寸（沿运动轨迹）
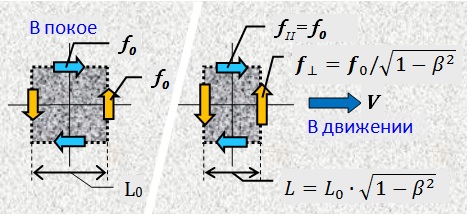将根据洛伦兹系数减小。为了使元件保持平衡，垂直于机芯的力必须以完全相同的比率增加。图7。
平行于运动的力的大小不会改变。在以下公式中，力的矢量展开中应考虑力相对于运动方向的定向依赖性。
注意，通过施加的力将身体加速到一定速度，这相应地做一些工作，从而增加了身体的能量。和空间中分散的物体与静止的物体有什么区别？根据Lorentz压缩超频的事实。在第1章中，针对给定点周围的点轨迹（GMT）导出了一个公式，从该公式中，它们具有相同的物理场交互时间。该GMT证明是根据洛伦兹在运动方向上压缩的椭圆体。现在让我们注意一个事实，该椭圆体的体积W与洛伦兹收缩成比例地减小。这反映在下面的公式（1）中。现在让我们做一个非常奇妙的假设，即当物体加速时，力的作用是花在压缩它所占据的空间上，然后在自由移动中保持不变。至少，这种假设并不比科学界认为空间会弯曲或膨胀的假设更糟。
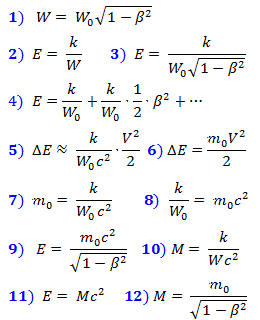假设此能量E与将公式（1）替换为公式（2）或公式（3）时可压缩的体积成反比。
我们将E从（3）扩展到泰勒级数（4），其中（5）是低速时第一近似中速度的能量增量。但是在低速时，它也等于（6）。比较（5）和（6），我们得到（7）和（8）。将（8）代入（3），我们得到（9），它将物体在压缩空间中的能量与其静止质量联系起来。
让我们用公式（10）表示相对论质量，然后用（2）代替，得到与质量和能量相关的众所周知的表达式（11）。比较（9）和（11），我们得到（12）。
质量只是压缩空间中消耗的能量的另一种表示形式。从这个意义上讲，它们是等效的。并且该物质仅在身体所占据的空间区域上“标记”。系统
总能量E的变化，即完全按照牛顿经典力学，空间的压缩能等于施加力的功，即每条路径的力乘积，系统的动量P的变化等于相同力及其作用时间的乘积。这些依赖性反映在公式（13）中。在将它们代入之后，将（11）中的能量和动量P的表达式从公式（14）中，
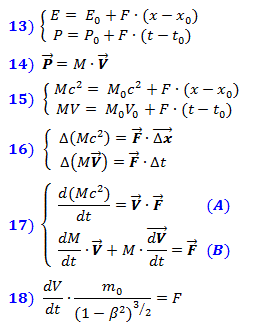我们得到方程式（15）的系统，它以矢量形式在（16）中以小增量的形式编写。然后，根据时间进行微分，我们记述了描述相对论动力学的微分方程组（17）。力F不需要区分，因为它是外部的，并且不依赖于系统变量的变化。将质量的表达式从（12）代入公式（A），我们得到众所周知的直线运动的相对论公式（18）。
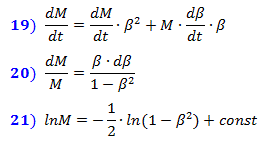从等式（17）的系统中，可以发现质量对速度的依赖性。将F从公式（B）代入公式（A），并将等式的两边除以c²，当沿着运动轨迹加速时，我们得到表达式（19）和（20）。从那里进行积分，我们得到表达式（21）。很容易看出，它相对论质量等于对数表达式（12），其中const等于静止质量m 0的对数。这意味着，质量对速度的这种依赖关系确保了公式（16、17）中的能量Mc²和动量M·V相对应。从这里也可以得出，我们先前假定为静止质量的值是一个常数，与速度无关，因为它写在原始公式（9）中。这意味着我们关于能量依赖于空间压缩程度的假设是正确的。
当然，空间压缩的主张不是很令人信服。如果假设空间是一个由粒子和物体组成的空容器，那么如何压缩空隙？空虚仍将是空虚。但是，科学允许自己谈论空白空间的曲率-公式需要它。但是，严格来说，它的空间是数学上的抽象。
但是我们可以相当合理地假设空间不是空的，而是充满了某种物质，假设它不是处于压缩状态，而是被我们认为是空虚的。...例如，当它处于压缩应力下时，我们将具有材料粒子和物体。当它们处于静止状态时，该物质的一部分的压缩程度（能量）对应于身体的静止质量，并且随着其加速度，身体的压缩程度（能量）和相应的质量均增加。
并且在这种物质环境中，决定粒子的位置和相互作用的物理场（直到“非常非常多”的主场，我们继续幻想，结果将成为从其环境中聚焦场的现象，没有它们就不存在），它们可能会以特定的速度存在并传播），其静止和运动能量取决于它们所占据的原始物质区域的压缩程度。其实，相对论动力学方程只是描述了原始物质中这些应力不均匀性（物质）的运动。如我们所见，与迈克尔逊的实验和洛伦兹变换没有矛盾。