资料来源：unsplash.com

，曾三届获得世界一级方程式冠军的杰基·斯图尔特（Jackie Stewart）表示，了解赛车有助于他成为更好的驾驶员：“赛车手不必是工程师，而是对机械的兴趣。” LMAX Disruptor的

创建者Martin Thompson 将此概念应用于编程。简而言之，了解底层硬件将提高您在设计算法，数据结构等方面的技能。Mail.ru云解决方案团队翻译了一篇文章，深入研究了处理器设计，并研究了如何理解某些CPU概念可以帮助您做出更好的决策。

基础

现代处理器基于对称多处理（SMP）的概念。处理器的设计方式是，两个或多个内核共享一个公共内存（也称为主存储器或随机存取存储器）。

此外，为了加快内存访问速度，处理器还具有多个缓存级别：L1，L2和L3。确切的体系结构取决于制造商，CPU型号和其他因素。但是，大多数情况下，L1和L2高速缓存在每个内核本地运行，而L3在所有内核之间共享。

SMP体系结构

高速缓存离处理器核心越近，访问延迟和高速缓存大小越低：

快取	延迟	CPU周期	规模
L1	〜1.2纳秒	〜4	32至512 KB
L2	〜3纳秒	〜10	介于128 KB和24 MB之间
L3	〜12纳秒	〜40	2至32 MB之间

同样，确切的数字取决于处理器型号。粗略估计，如果访问主内存需要60 ns，则访问L1的速度大约快50倍。

在处理器世界中，存在链路局部性的重要概念。当处理器访问特定的内存位置时，很有可能：

在不久的将来它将指向相同的存储位置-这是时间局部性的原理。
他将提到附近的存储单元-这是按距离局部的原则。

时间局部性是CPU缓存的原因之一。但是如何使用距离局部性？解决方案-将高速缓存行复制到那里，而不是将一个存储单元复制到CPU高速缓存。高速缓存行是内存的连续段。

缓存行大小取决于缓存级别（以及处理器型号）。例如，这是我的机器上的L1高速缓存行的大小：

$ sysctl -a | grep cacheline
hw.cachelinesize: 64

处理器没有将单个变量复制到L1高速缓存，而是在此处复制了连续的64字节段。例如，它不会复制Go切片中的单个int64元素，而是会复制该元素以及另外七个int64元素。

Go中缓存行的特定用途

让我们看一个具体的示例，演示处理器缓存的好处。在下面的代码中，我们添加了两个int64元素的平方矩阵：

func BenchmarkMatrixCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[i][j]
            }
        }
    }
}

如果matrixLength等于64k，它将产生以下结果：

BenchmarkMatrixSimpleCombination-64000                     8  130724158 ns/op

现在，matrixB[i][j]我们将添加matrixB[j][i]：

func BenchmarkMatrixReversedCombination(b *testing.B) {
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i++ {
            for j := 0; j < matrixLength; j++ {
                matrixA[i][j] = matrixA[i][j] + matrixB[j][i]
            }
        }
    }
}

这会影响结果吗？

BenchmarkMatrixCombination-64000                           8  130724158 ns/op
BenchmarkMatrixReversedCombination-64000                   2  573121540 ns/op

是的，确实如此，而且从根本上来说是这样！如何解释呢？

让我们尝试绘制正在发生的事情。蓝色圆圈表示第一个矩阵，粉红色圆圈表示第二个矩阵。设置时matrixA[i][j] = matrixA[i][j] + matrixB[j][i]，蓝色指针位于位置（4.0），粉红色指针位于位置（0.4）：

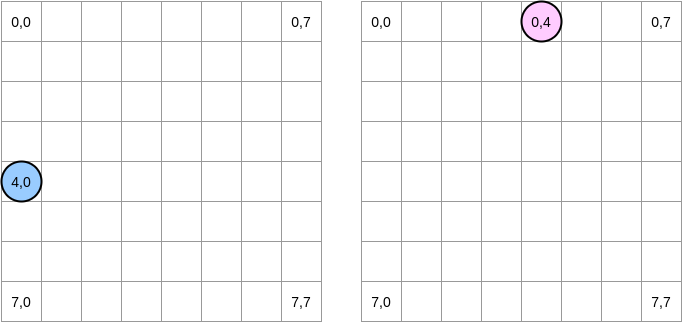
注意。在此图中，矩阵以数学形式表示：横坐标和纵坐标，位置（0,0）在左上角。在存储器中，矩阵的所有行都按顺序排列。但是，为清楚起见，让我们看一下数学表示形式。此外，在以下示例中，矩阵大小是缓存行大小的倍数。因此，高速缓存行不会在下一行“赶上”。听起来很复杂，但是这些示例将使所有内容变得清晰。

我们如何遍历矩阵？蓝色指针向右移动，直到到达最后一列，然后在位置（5,0）移至下一行，依此类推。相反，粉红色指针向下移动，然后移至下一列。

当粉红色指针到达位置（0.4）时，处理器将缓存整个行（在我们的示例中，缓存行大小为四个元素）。因此，当粉红色指针到达位置（0.5）时，我们可以假定该变量已存在于L1中，对吗？

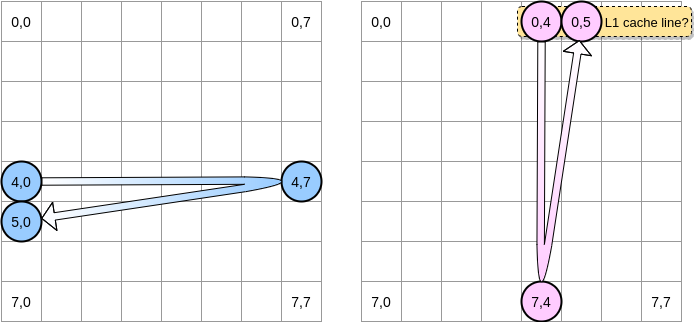
答案取决于矩阵的大小：

如果矩阵与L1的大小相比足够小，则是的，元素（0.5）将已经被缓存。
否则，缓存行将在指针到达位置（0.5）之前从L1中删除。因此，它将生成高速缓存未命中，并且处理器将必须以其他方式（例如，通过L2）访问变量。我们将处于这种状态：

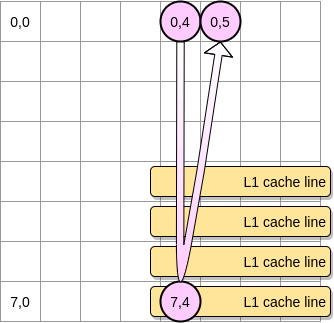
受益于L1的矩阵需要多小？让我们数点。首先，您需要了解L1缓存的大小：

$ sysctl hw.l1dcachesize
hw.l1icachesize: 32768

在我的机器上，L1缓存为32,768字节，而L1缓存行为64字节。这样，我可以在L1中存储多达512条缓存行。如果我们使用512元素矩阵运行相同的基准测试该怎么办？

BenchmarkMatrixCombination-512            1404   718594 ns/op
BenchmarkMatrixReversedCombination-512    1363   850141 ns/opp

尽管我们固定了差距（在64k矩阵上，差距约为4倍），但我们仍然可以看到微小的差距。有什么事吗在基准测试中，我们使用两个矩阵。因此，处理器必须保留两者的高速缓存行。在理想的世界中（没有其他应用程序在运行），L1缓存中第一个矩阵的数据填充了50％，第二个矩阵的数据填充了50％。如果我们将矩阵的大小减半以使用256个元素怎么办：

BenchmarkMatrixCombination-256             5712   176415 ns/op
BenchmarkMatrixReversedCombination-256     6470   164720 ns/op

最后，我们到达了两个结果（几乎）相等的地步。

. ? , Go. - LEA (Load Effective Address). , . LEA .

, int64 , LEA , 8 . , . , . , () .

现在-在矩阵较大的情况下如何限制缓存未命中的影响？有一种方法称为嵌套循环的优化（循环嵌套优化）。为了充分利用缓存行，我们应该仅在给定的块内进行迭代。

让我们在示例中将一个块定义为4个元素的正方形。在第一个矩阵中，我们从（4.0）迭代到（4.3）。然后转到下一行。因此，我们仅将第二个矩阵从（0.4）迭代到（3.4），然后再转到下一列。

当粉红色指针越过第一列时，处理器将存储相应的缓存行。因此，遍历块的其余部分意味着利用L1：

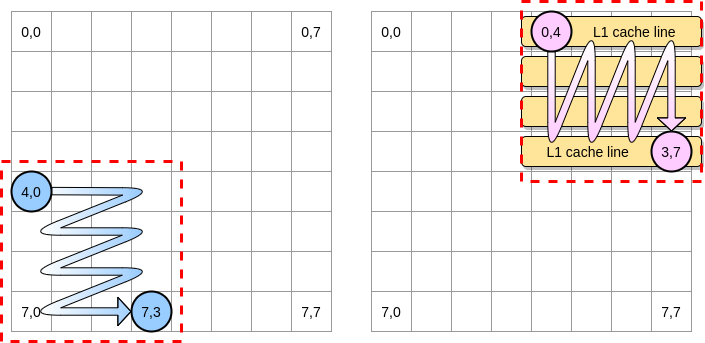
让我们在Go中编写该算法的实现，但是首先我们必须仔细选择块大小。在前面的示例中，它等于高速缓存行。它不能更小，否则我们将存储无法访问的元素。

在Go基准测试中，我们存储int64元素（每个元素8个字节）。缓存行为64字节，因此可以容纳8个项目。然后，块大小值必须至少为8：

func BenchmarkMatrixReversedCombinationPerBlock(b *testing.B){
    matrixA := createMatrix(matrixLength)
    matrixB := createMatrix(matrixLength)
    blockSize := 8

    for n := 0; n < b.N; n++ {
        for i := 0; i < matrixLength; i += blockSize {
            for j := 0; j < matrixLength; j += blockSize {
                for ii := i; ii < i+blockSize; ii++ {
                    for jj := j; jj < j+blockSize; jj++ {
                        matrixA[ii][jj] = matrixA[ii][jj] + matrixB[jj][ii]
                    }
                }
            }
        }
    }
}

与迭代整个行/列时相比，我们的实现现在快了67％以上：

BenchmarkMatrixReversedCombination-64000          2  573121540 ns/op
BenchmarkMatrixReversedCombinationPerBlock-64000  6  185375690 ns/op

这是第一个证明了解CPU缓存操作可以帮助设计更高效算法的示例。

虚假分享

现在，我们了解了处理器如何管理内部缓存。快速总结：

按距离的局部性原则迫使处理器不仅要占用一个存储器地址，而且要占用一条缓存行。
L1高速缓存在一个处理器内核本地。

现在，让我们讨论一个具有L1缓存一致性的示例。主存储器存储两个变量var1和var2。一个核心上的一个线程访问var1，而另一个核心上的另一个线程访问var2。假设两个变量都是连续的（或几乎连续的），我们最终会遇到var2两个缓存都存在的情况。

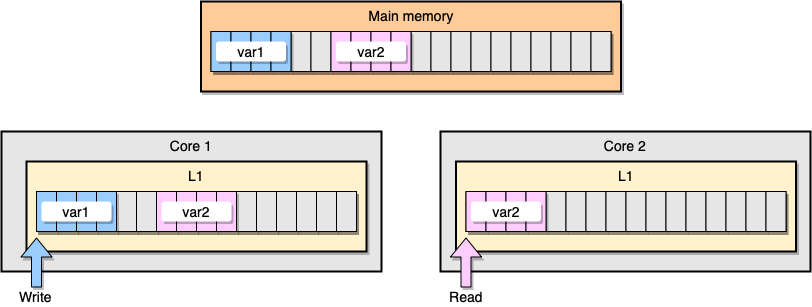
示例L1缓存

如果第一个线程更新其缓存行会发生什么？它可以潜在地更新其字符串的任何位置，包括var2。然后，当第二个线程读取时var2，该值可能不一致。

处理器如何使缓存保持一致？如果两条高速缓存行具有共享地址，则处理器会将它们标记为共享地址。如果一个线程修改了共享行，则将两者都标记为已修改。需要内核之间的协调以确保高速缓存的一致性，这可能会大大降低应用程序性能。这个问题称为虚假共享。

让我们考虑一个特定的Go应用程序。在此示例中，我们一个接一个地创建两个结构。因此，这些结构在内存中必须是顺序的。然后我们创建两个goroutine，每个goroutine都引用自己的结构（M是等于一百万的常数）：

type SimpleStruct struct {
    n int
}

func BenchmarkStructureFalseSharing(b *testing.B) {
    structA := SimpleStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

在此示例中，第二结构的变量n仅可用于第二goroutine。但是，由于结构在内存中是连续的，因此该变量将出现在两条高速缓存行中（假定两个goroutine都安排在单独内核上的线程上，不一定是这种情况）。这是基准测试结果：

BenchmarkStructureFalseSharing         514    2641990 ns/op

如何防止虚假信息共享？一种解决方案是完整的内存（内存填充）。我们的目标是确保两个变量之间有足够的空间，以便它们属于不同的缓存行。

首先，让我们在声明变量后填充内存，以创建先前结构的替代方案：

type PaddedStruct struct {
    n int
    _ CacheLinePad
}

type CacheLinePad struct {
    _ [CacheLinePadSize]byte
}

const CacheLinePadSize = 64

然后，我们实例化这两个结构，并继续在单独的goroutine中访问这两个变量：

func BenchmarkStructurePadding(b *testing.B) {
    structA := PaddedStruct{}
    structB := SimpleStruct{}
    wg := sync.WaitGroup{}

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        wg.Add(2)
        go func() {
            for j := 0; j < M; j++ {
                structA.n += j
            }
            wg.Done()
        }()
        go func() {
            for j := 0; j < M; j++ {
                structB.n += j
            }
            wg.Done()
        }()
        wg.Wait()
    }
}

从内存的角度来看，此示例应看起来像这两个变量是不同的缓存行的一部分：

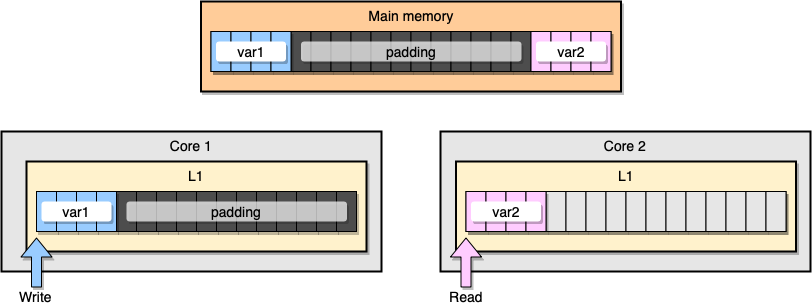
内存填充

让我们看一下结果：

BenchmarkStructureFalseSharing         514    2641990 ns/op
BenchmarkStructurePadding              735    1622886 ns/op

第二个带有内存填充的示例比我们的原始实现快40％。但也有一个缺点。该方法加快了代码的速度，但是需要更多的内存。

在优化应用程序时，喜好机制是一个重要的概念。在本文中，我们看到了一些示例，这些示例说明了对CPU的理解如何帮助我们提高了程序速度。

还有什么要读的：

Go和CPU缓存

基础

Go中缓存行的特定用途

虚假分享

More articles: