-大家好,我叫Rishat。我从事Yandex搜索质量的工作已经近三年了。但是今天,我不想谈论工作,而是谈论我在业余时间的工作。我从事量子信息学研究,但实际上-包括量子模型在内的各种计算模型。
量子信息学现在是一个有趣的领域。在这里投入了大量的精力,已经做了很多工作。在我的报告中,我将尝试使你们中的一些人感兴趣。也许您当中有一位很酷的ML工程师想要进行量子机器学习,或者只是一位强大的算法专家可以朝这个方向投资。它将是伟大的,因为未来即将到来。
我必须马上说我不是物理学家。当然,你们当中有些人比我更了解物理学中的所有这些过程。因此,我几乎不说物理学。
我希望您能稍微记住代数,记住向量是什么,以及如何将向量乘以矩阵。

我的报告将如何组织?首先,我们将谈论一些历史,关于一切的起源,以便自信地展望未来。然后,我们将看到可以在哪里应用它,现在处于什么状态,现在是否可以用手进行某些操作。我们将编写第一个可以在量子计算机上运行的Python程序。然后,作为奖励,我将向您展示一些算法示例,在这些示例中,量子计算与传统算法相比,可以帮助实现无与伦比的性能。

它是如何开始的?来自这个年轻人。这就是艾伦·图灵(Alan Turing),可以放心地称他为计算机科学之父或计算机科学之父,我们现在赖以生存的那个人就是赚钱的人。在1930年代,图灵提出了一种计算模型,我们现在将其称为可编程计算机。但是有人会认出这个人吗?

更加困难。他的姓氏经常与图灵的姓氏相邻。这是阿隆佐·丘奇(Alonzo Church),他还处理可计算性问题,甚至在图灵提出自己的计算模型之前就处理了一点。但是图灵的作品变得越来越受欢迎。总的来说,教会在某个时候是图灵的科学顾问。两者合计,它们的名称通常与本论文相关。
Church-Turing论文说:任何过程都可以在Turing机器上有效地建模。这是30年代末-40年代初,一切都很好。大约30年以来,一切都非常好,直到这两个人出现。有人认识他们吗?

这已经是70年代了,非常接近现在。它们的姓氏经常在密码学课程中找到。这些是罗伯特·南丁格尔和沃尔克·斯特拉森。这两个人以提出用于检查数字是否简单的概率算法而闻名,即Solovey-Strassen测试。
这对我们来说是非常重要的一点,因为到目前为止,我们说任何算法过程都可以在图灵机上建模。但是现在事实证明,他们的算法无法建模。它是概率性的,图灵机中没有类似的东西。
我必须快速修复,并说任何过程都可以在概率图灵机上建模。这已经不是很酷了,可以肯定的是,你们中的一个人的胸部被捏了一下。您以为:如何?现在我们说“概率论”,十年之内还会发现其他问题,而其他一些问题则必须纠正。这不是很愉快。但是,您和我当然并不孤单。

还有另一个年轻人-David Deutsch。他也想知道:怎么回事?如何生活?他是一位受过训练的物理学家,毕生致力于物理学。我决定从物理学的角度解决这个问题。他说:让我们尝试证实,得到一些东西,以便自然界告诉我们,确实如此。那时自然已经(我们仍然相信)说过,这是量子力学。因此,我们开始寻找量子力学的答案。正是借助David Deutsch和他的第一个算法,量子信息学才开始出现。
这是一次对历史的细微考察,以使您了解:这并非突如其来。从理论上讲,这个领域确实存在着真正的问题,这些问题折磨着一切的开始。
但是,一切都只是在理论层面上吗?从数学的观点来看,总的来说,没有任何问题。在数学上,我们对量子计算机的工作原理一无所知。现在已经有不同配置,以不同方式工作的真实量子计算机。总的来说,这是工程上的挑战。
例如,在我们的研究所,我们有一个处理量子信息学的完整部门。有数学家和物理学家。物理学家现在非常关注量子信息的长期存储问题。它与我们的硬盘非常相似,但是我们希望将量子信息存储在此处。

整个经济的用途是什么?当然,首先想到的是过程的建模,因为世界是量子力学的。而且,如果我们使用量子计算机来模拟过程,化学反应或其他任何东西,那么它将在计算上便宜得多。
第二个非常大的部分是量子机器学习,现在已经投入大量精力。量子计算将极大地帮助自己加快学习过程并改进算法。这里有很多工作。现在,例如,我们的量子小组正在与来自中国的科学家合作。他是一位非常强大的ML工程师,我们有点量子偏差,试图提出一些建议。
第三件事是几个月前的炒作。现在,也许炒作已经沉睡了,但是甚至还有整个量子区块链。它是我的好朋友和好朋友发明的。这就是我,我有点自豪地说。
但是我们没有量子计算机。不幸的是,我们不能像使用Python那样容易地回家运行程序。
该怎么办?当我写我的第一学期论文时,我在想三年级的工作。我在写量子计算模拟器。当然,每个人都编写模拟器,并且每个人都以某种方式使用它们。在我四年级的时候,我写了一个模拟器来模拟干扰,噪音等。然后我很无聊。
我尝试在搜索引擎中进行搜索,并意识到有很多模拟器。这里有一些链接,它们非常简单有趣:
- github.com/quantumlib/Cirq
- github.com/artiste-qb-net/qubiter
- code.google.com/archive/p/pyqu
- qiskit.org
但我想在qiskit停下来。他很特别,与众不同。比?
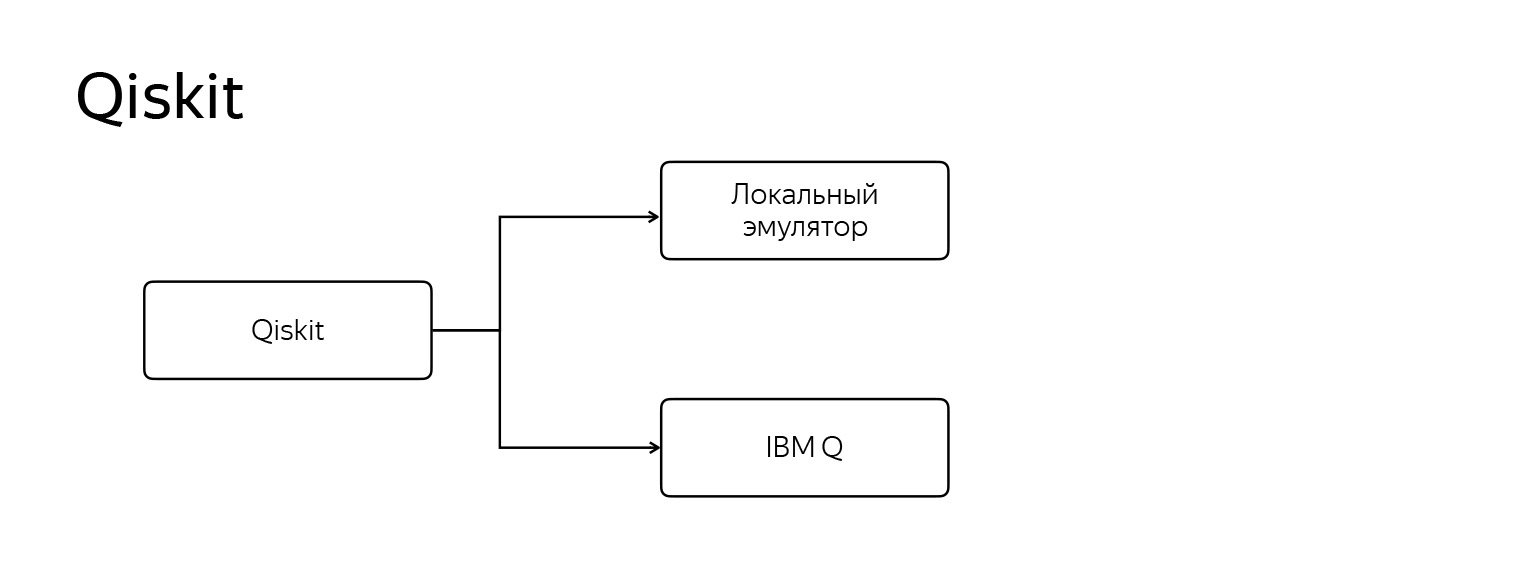
它以两种模式工作。首先,像其他所有人一样,这是一个常规的本地模拟器。第二种是在真正的IBM Q Quantum计算机上运行程序,看起来像这样。

现在,它是一个保持极低温度的整个机筒-大约3毫升。它是非常冷的。IBM提供了基于云的功能,可以在该计算机上直接连接和运行您的代码。
当然,他以特殊的方式编译命令等。它甚至如何工作?有几种这样的计算机安装可供一般访问。其中之一是5 qubit,有15 qubit,16 qubit,甚至20 qubit可供我们使用。这大约是20位普通的经典信息,但是已经有些东西了。
当然,在座的许多人都认为:就是这样,我想要!但是您必须记住一点数学。就像我答应的那样,有一点代数,但只有一点。
要在量子计算机上开始编程,您需要了解什么是量子位。它只是二维向量空间中的向量。但是由于我们在谈论向量空间,所以它们有基础。

基础看起来像这样。在代数课程中,有两个向量列和一个单位基准(标准),其表示如下:
和
。在这些尖括号中,狄拉克(Dirac)的注释中有一个标准的注释。
也就是说,为了不让您感到困惑,我将继续这样缩短。
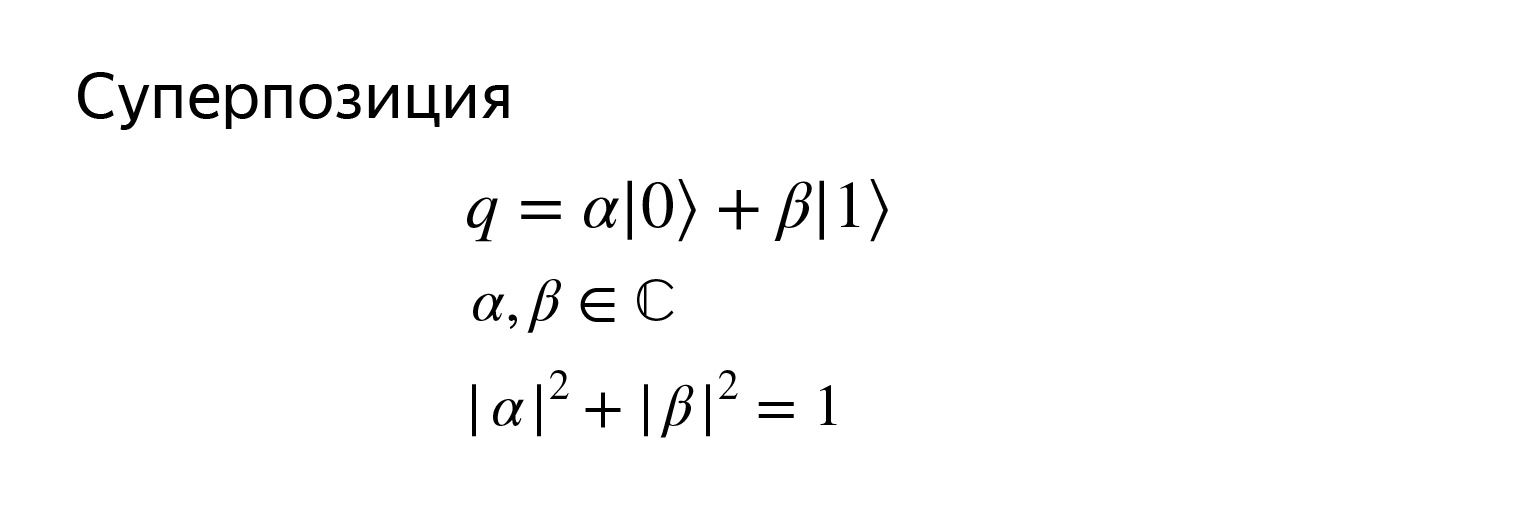
由于它是向量,因此其状态可以这样写。量子位q是两个基向量的叠加,其中α和β是复数,但不是绝对的任何数,但是它们的平方模之和等于1。
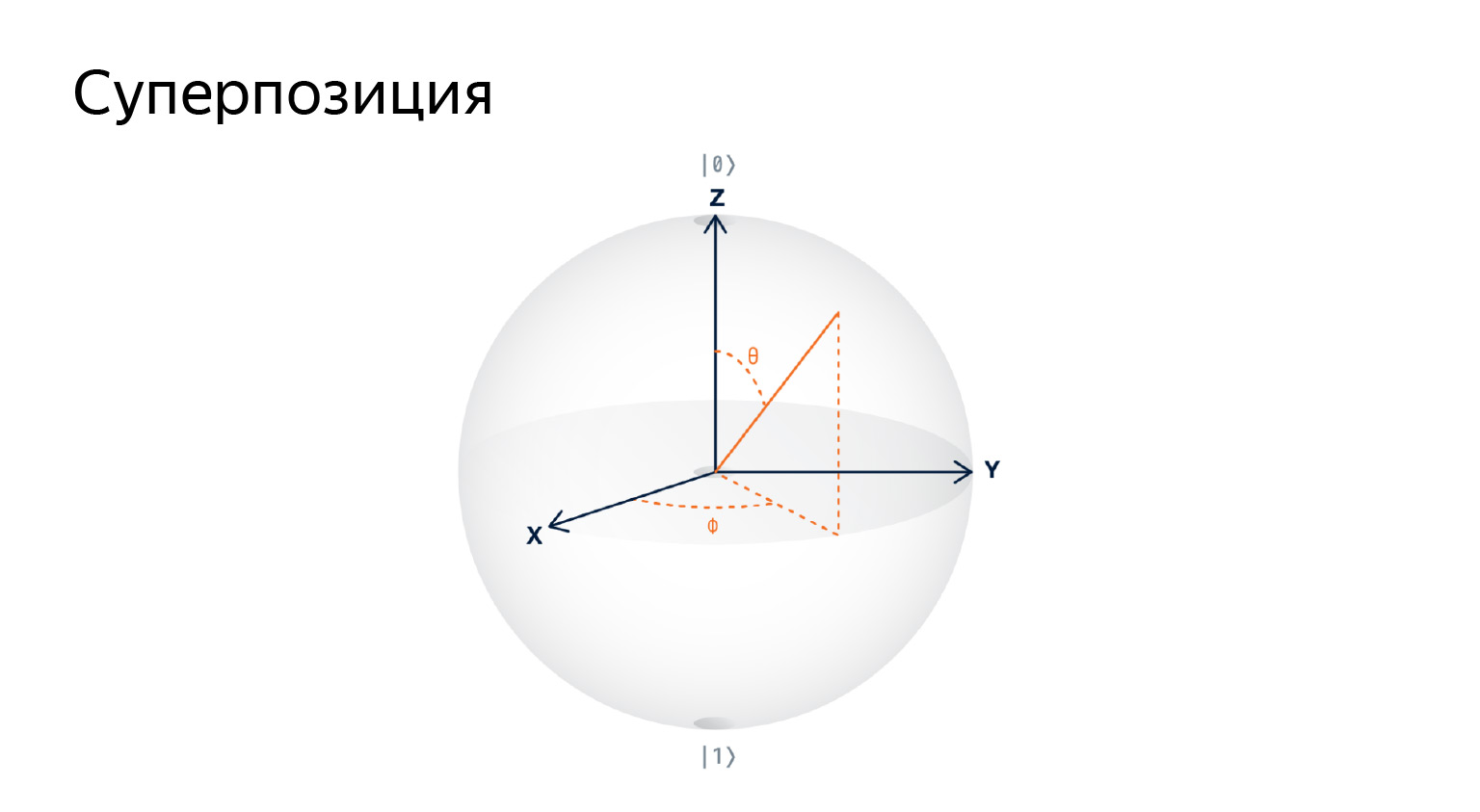
如果我们尝试画出这个东西,我们会得到一个量子位是三维球体上的向量。无限量的信息可以存储在一个qubit中,因为它只是一个向量,其中有无限量。
您不需要关注图片,这只是一种吸引人们注意的可视化技术。
我们谈论了量子位。最重要的是,量子位是向量。在复杂向量空间中的向量。你能做什么呢?
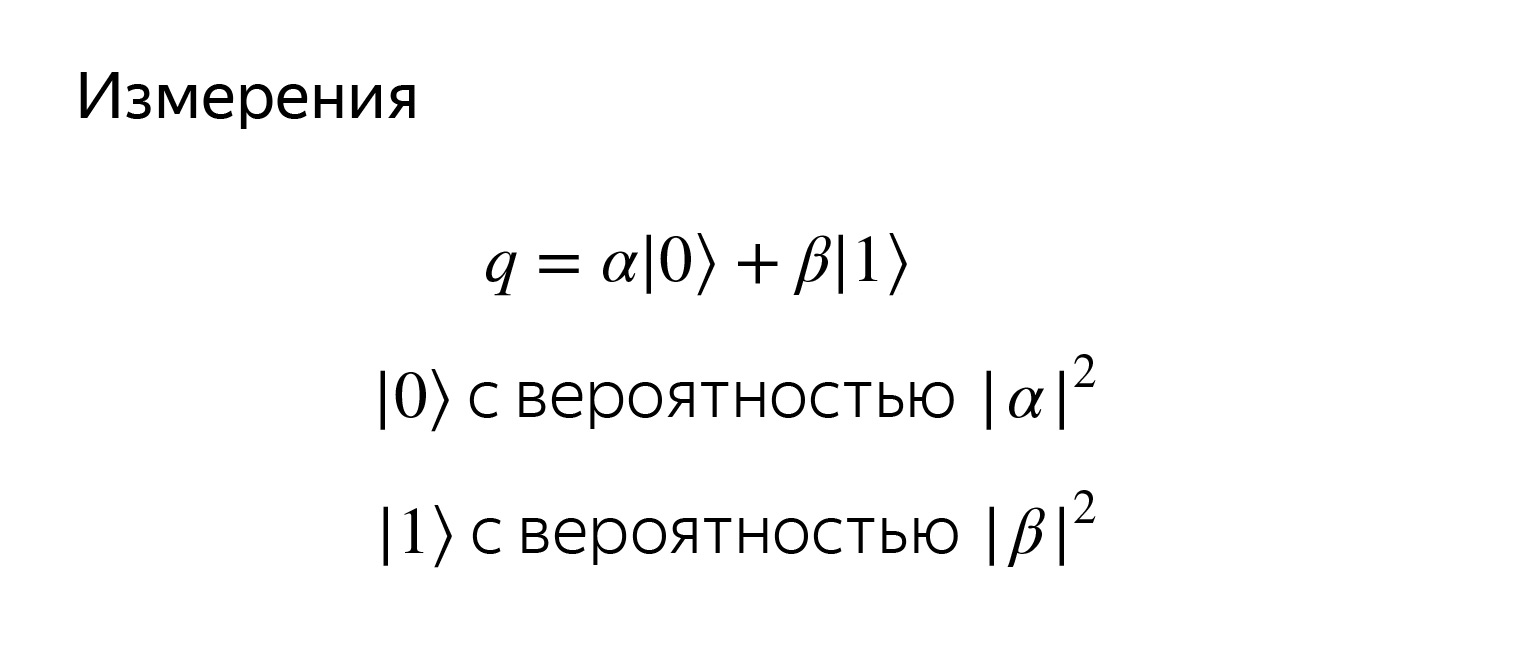
我们以前要做的第一件事就是尝试计算变量的值,例如在Python中。我们想读取量子位处于什么状态。但是我们永远不会知道α和β的确切含义。
如果我们尝试查看一个量子比特,请读取它,然后得到具有相应概率的零或一。概率只是对相应基向量的投影。
我们可以做的第二件事是,例如,克隆一个量子位。我们称之为将一个变量分配给另一个变量。不幸的是,这在量子世界中是无法做到的。

没有赋值操作,这与我刚才说的很相关:我们甚至无法查看确切的值。这是一个根本的结果。这很简单地证明了:实际上是两行比较。
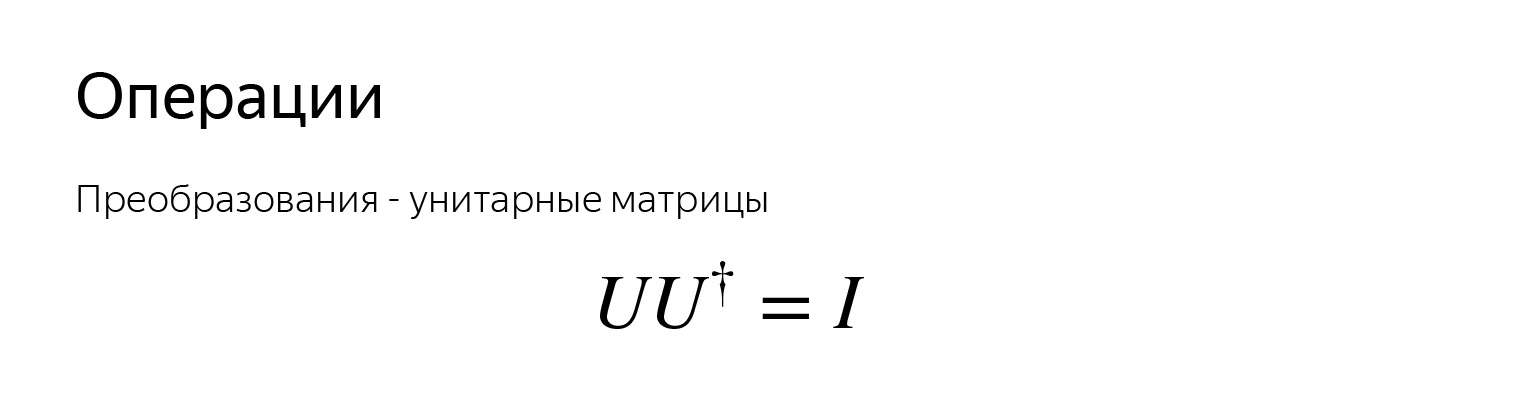
有一个我们无法阅读的量子位,我们无法克隆。你到底能做什么?
量子位是向量。可以获取矢量并围绕球旋转。要旋转,您可以考虑进行旋转的矩阵。对量子位的所有运算都是矩阵。他们被称为单一的。
单一的-为了满足这样的条件,在这里以狡猾的方式写出来。此图标表示转置和复共轭矩阵。此属性非常重要,这意味着任何运算都存在反函数。也就是说,无论我们如何扭曲向量,都可以始终将其返回到其先前位置。总是存在反向操作。
让我们看看可以进行哪些操作。在经典情况下,我们已经习惯了。有一个零,您可以将其变成一个,反之亦然。
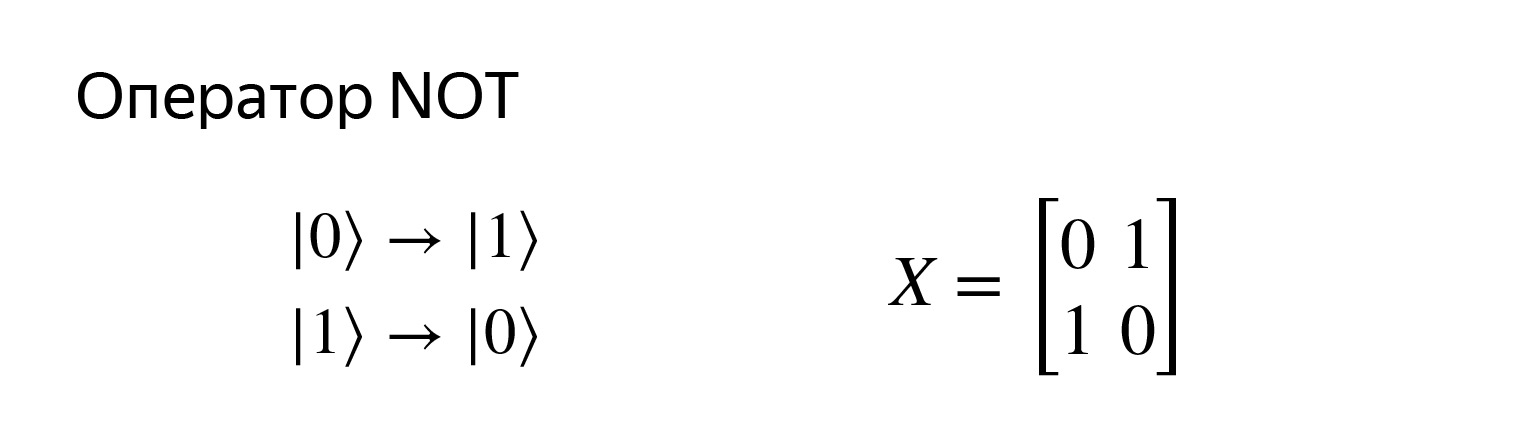
这是求反运算符,非常简单。用这样的矩阵记录。如果我们尝试相乘,就会得到我们想要的。
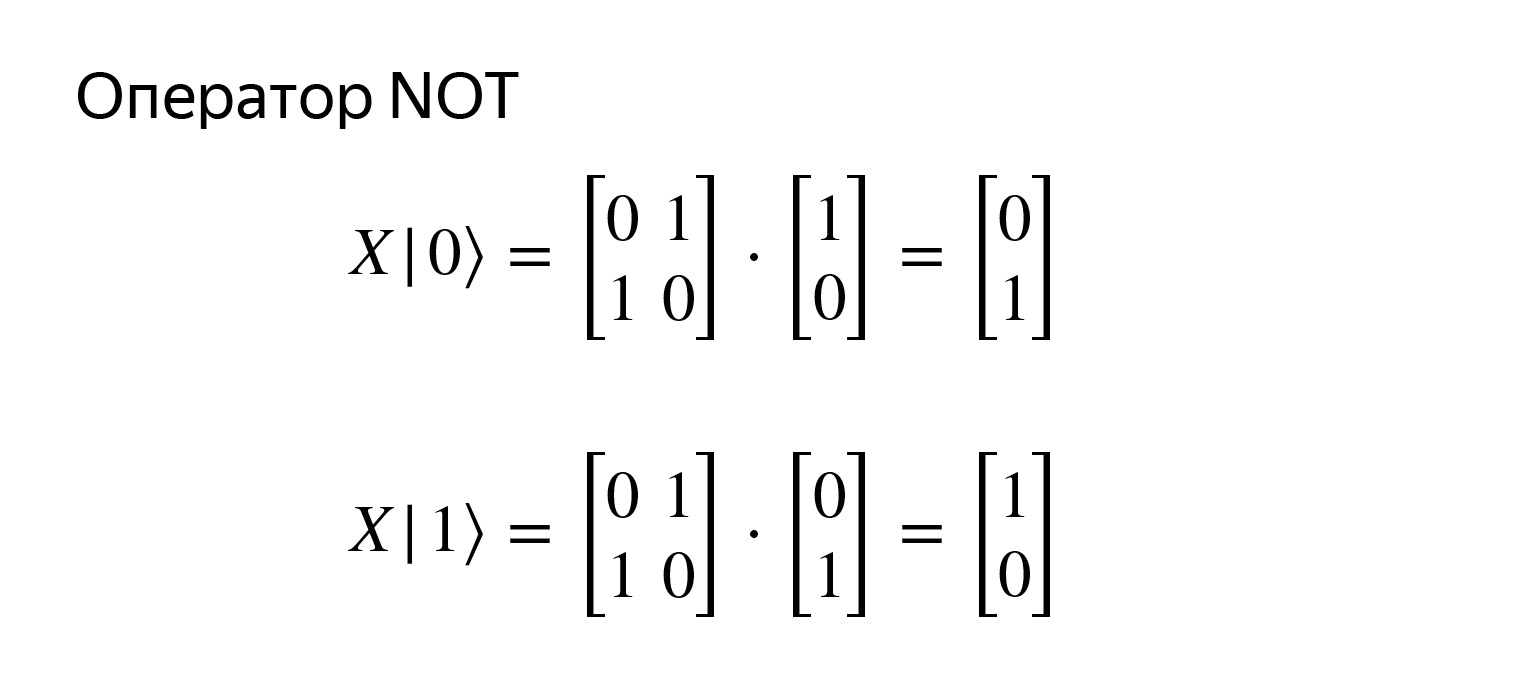
我什至在这里画了它。没什么复杂的。取反运算符具有标准符号X运算符,想一想,它只是绕其中一个轴的旋转。并且有运算符Y和Z绕其他轴旋转,但是现在这并不那么重要。
而且我们已经可以在将使量子位无效的量子计算机上运行我们的第一个程序。
但是,我们在量子计算机科学中当然很少用Python编写。我们更频繁地使用模式。

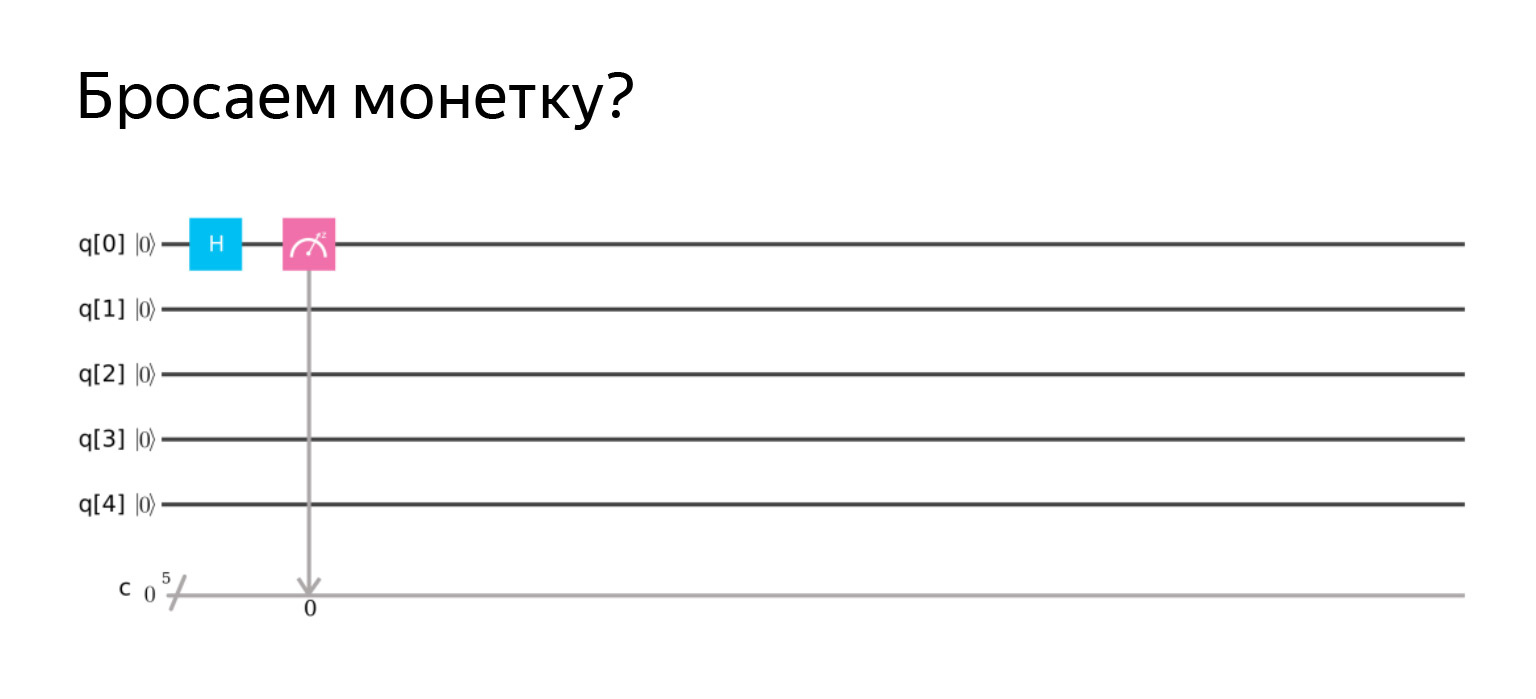
该图通常看起来像这样。水平线只是量子位值。我在这里画了五个。并且在块中-我们将执行的操作。
第一块。此处绘制了一个测量设备。这意味着我们只想测量第一个量子位中的内容。
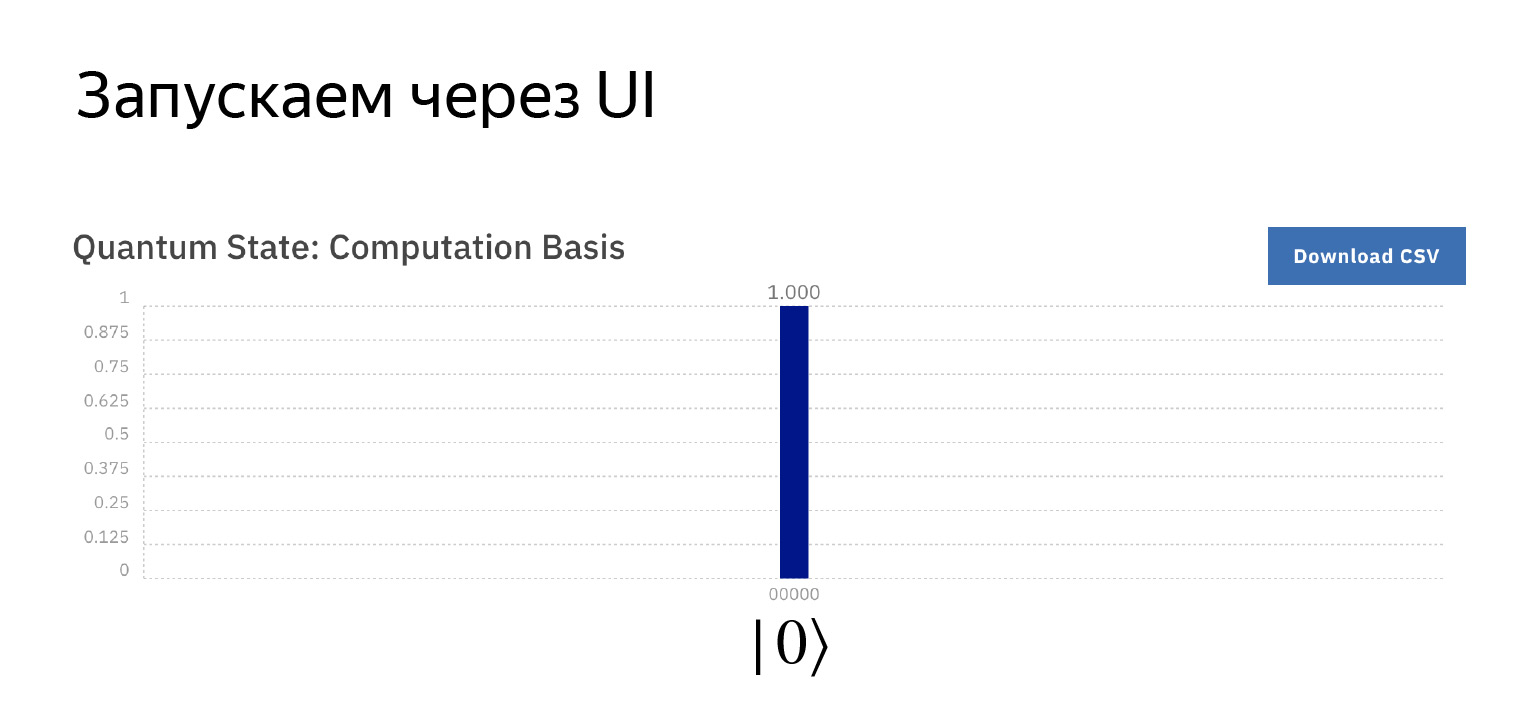
如果我们运行该程序,那么我们得到的可能性是1,那里的值为零,因为它们是在这种状态下初始化的,我们对它们不做任何事情。
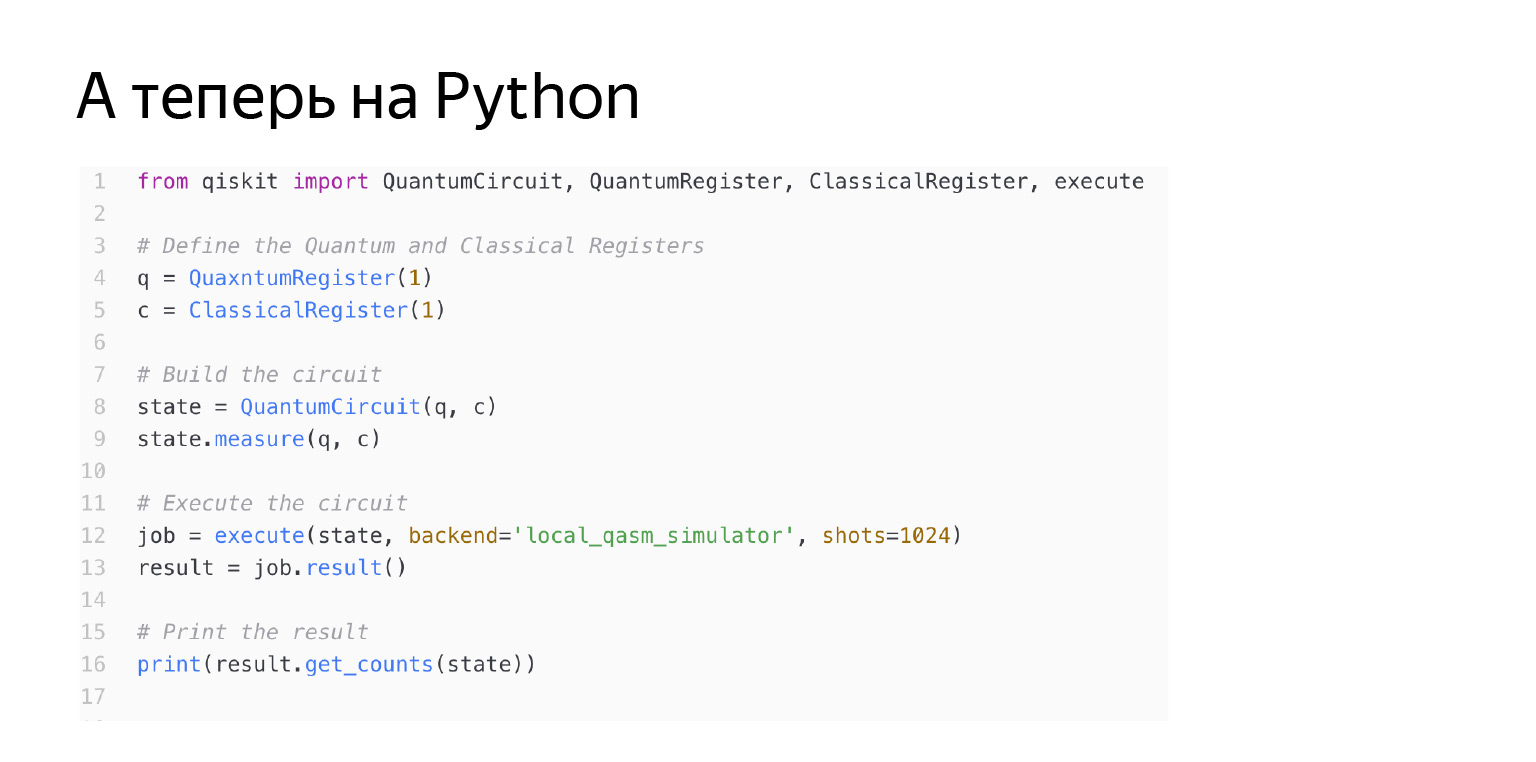
可以使用qiskit库用Python编写这样的东西。让我们逐行看看会发生什么。首先,我们启动量子寄存器。我正在从一个量子位打开它。和经典的寄存器。需要经典寄存器将测量结果写入某处。也就是说,我使用量子寄存器进行转换,结果是经典的1-零或一。然后,我创建自己的电路,该电路具有该量子经典量子比特。我只是说:让我们测量C中的q量子比特。让我们开始整个过程,一切都会好起来的。但是,细心的读者会看到:它说我的后端是本地模拟器。

IBM Q可以完成相同的操作,但是这里有更多代码。选择各种各样的设备来尽快响应我们,转移一些代币,这就是各种各样的事情。但是没有什么棘手的问题。

取反运算符也可以这样做。正如我所说的,这是X运算符。在图上看起来完全一样,让我们运行相同。
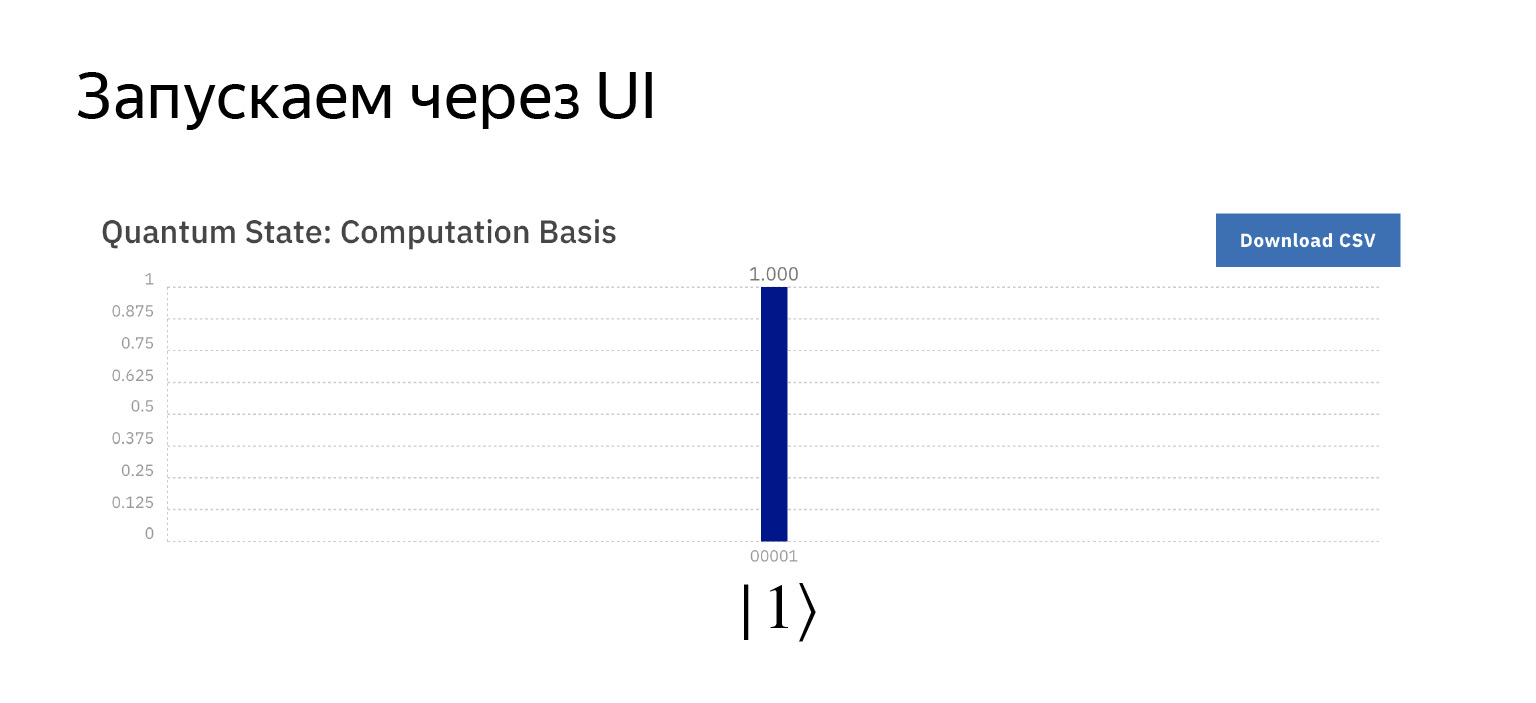
现在,按照计划,概率为一,我们得到一。没魔术
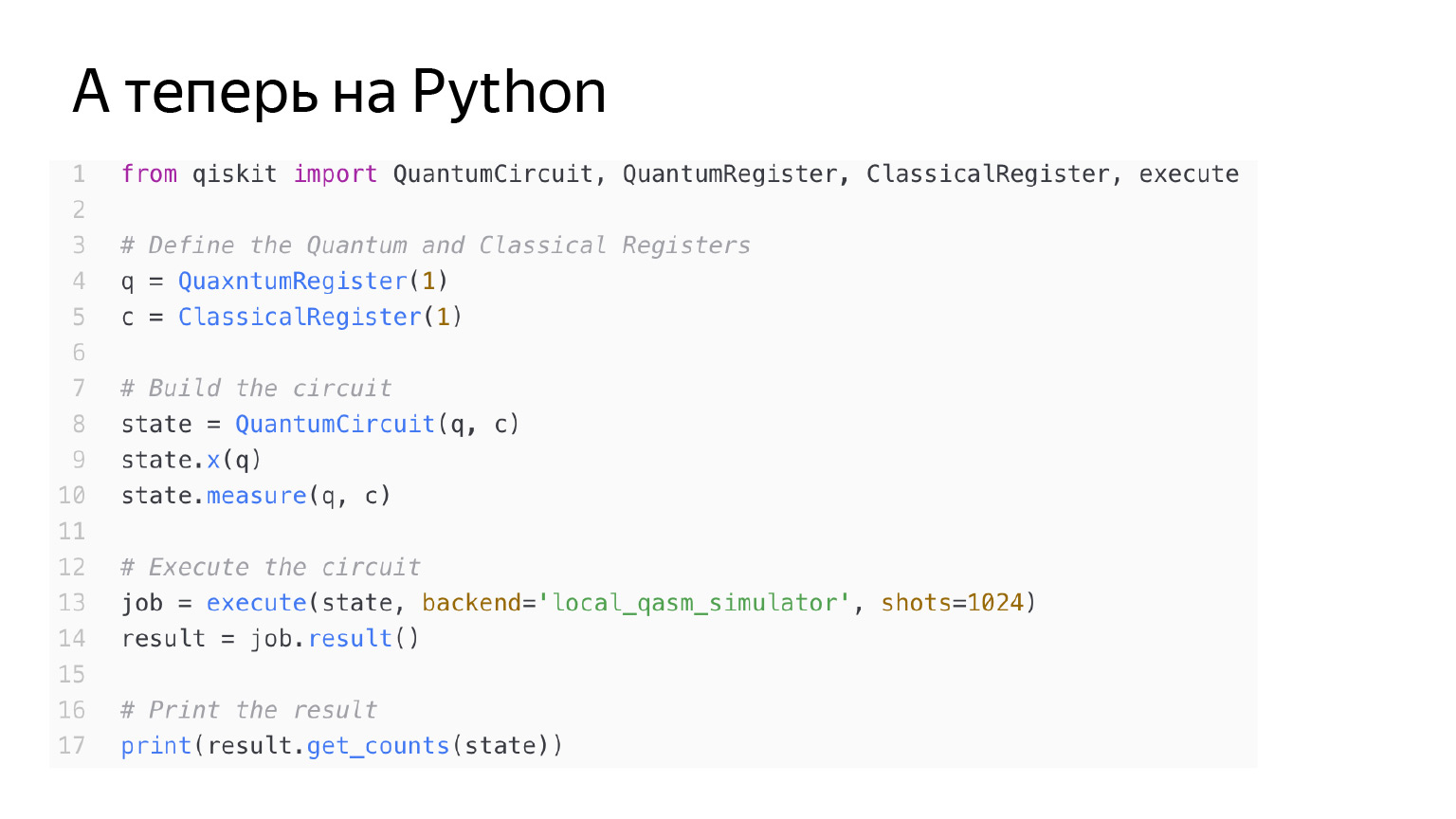
代码是一样的。只是在这里我还将X运算符应用于q量子位。
好的,让我们尝试进一步。
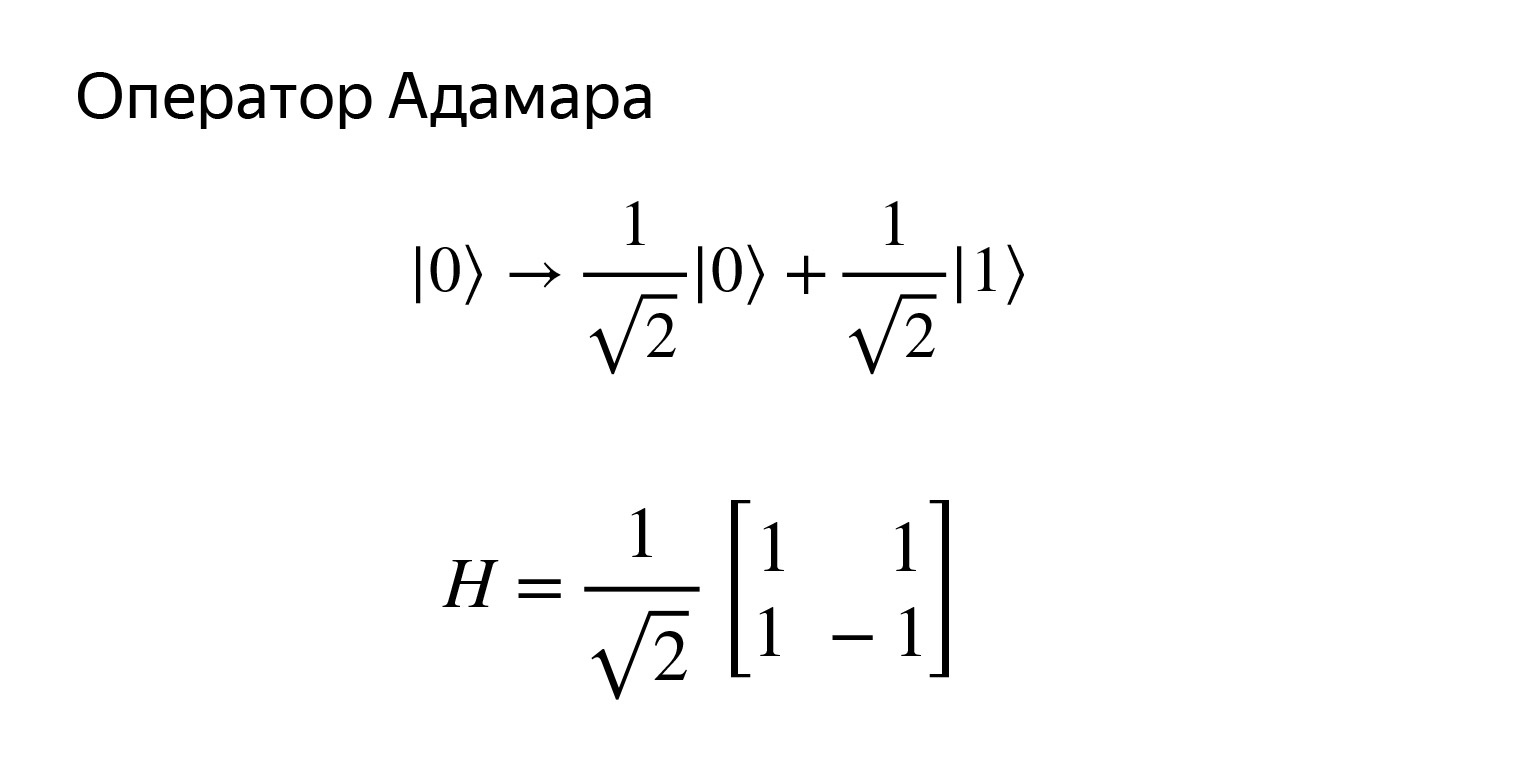
这里有一件非常棘手的事情。让我们尝试获得这种状态。这种状态非常有趣。我们将得到这样的叠加。如果我们尝试测量它,则以1/2的概率得到零或一。也就是说,这将是一个统一的叠加,我们可以得到任何东西。
可以推论什么是量子硬币抛掷。我们会说好的,概率为½时,我们得到零和一。矩阵看起来像这样。
易于检查,但我们当然不会。让我们画一个图。运营商H为了纪念Hadamard。
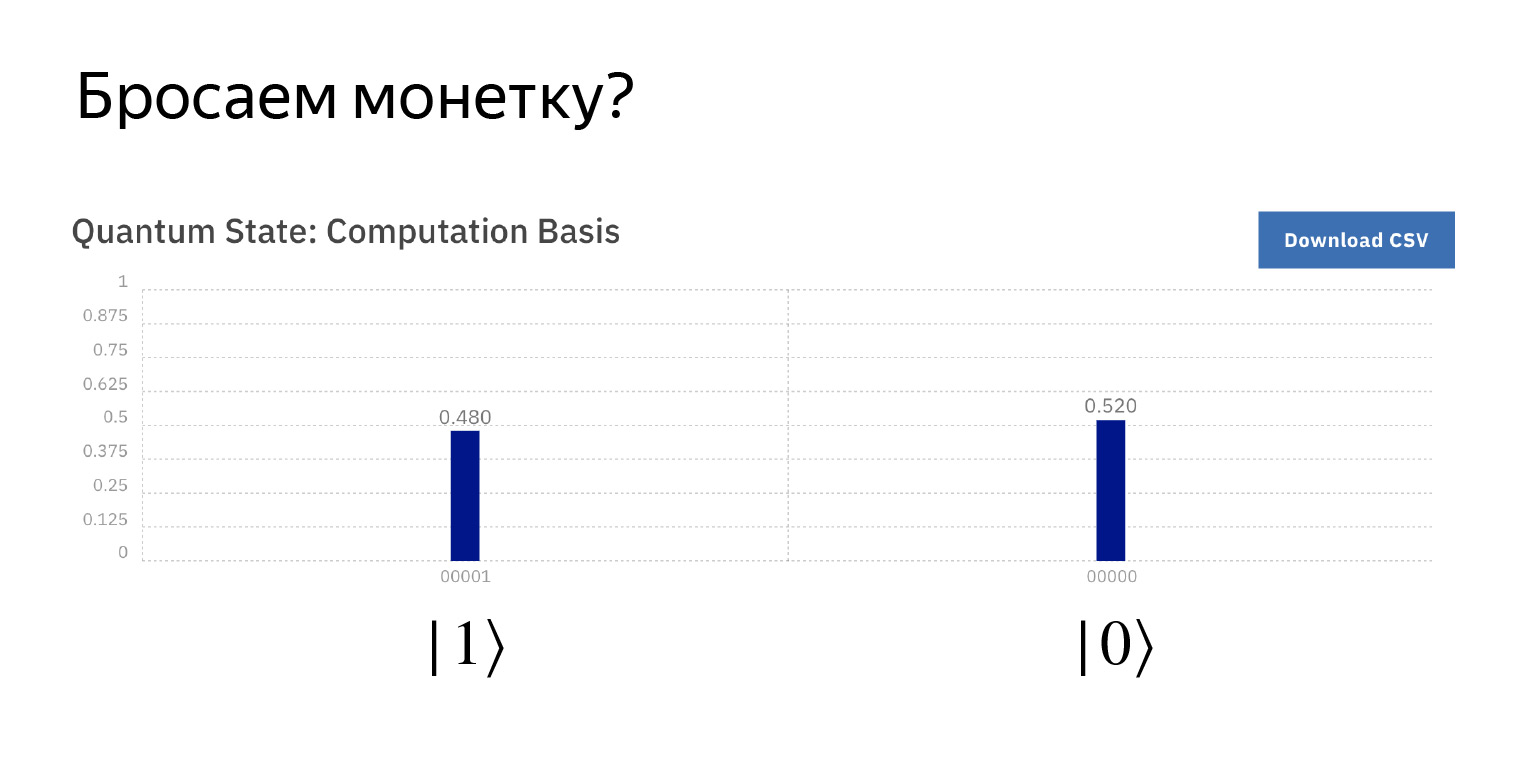
让我们测量并大致获得我们的期望。概率为½,0和1。多一点,少一点,但这就是它的工作原理。
这是Python代码,仅此而已,我们正在Python会议上。

有这样的叠加。我们对其应用Hadamard运算符并进行测量。
但是您可以掷硬币两次,我们都已经习惯了。如果您掷硬币两次,则不会改变。让我们尝试在量子情况下做到这一点。

我们连续两次应用Hadamard运算符,并且总是得到零。

也就是说,如果您两次掷出一枚量子硬币,由于哈达玛算子本身是逆的,因此您总是会得到零。如果自己乘,总会得到一。这是一件事。
因此,您可以用一个量子位来做某事。可以扭曲,扭曲和测量。让我们尝试添加更多的量子比特。在古典世界里我们习惯做什么?进行并执行简单的逻辑运算,即“或”和“与”。

在量子世界中,您不能这样做,因为它们不是完全可逆的。也就是说,在``与''运算中得到零,我们永远无法知道初始值是什么。
正如我所说,在量子世界中,运算是一个始终可逆的a矩阵。那么,您如何编程?我们习惯的一切都在崩溃。但是出现了新的英雄,这就是所谓的受控否定的操作者。

如果我们使用Python编写,它将看起来像这样。如果第一个量子位是一个,那么我们反转第二个量子位。这不是矩阵,这是运算符的外观。但原则上,我所说的是写在这里。在第一个量子位中存在统一性的地方,第二个量子位被反转。
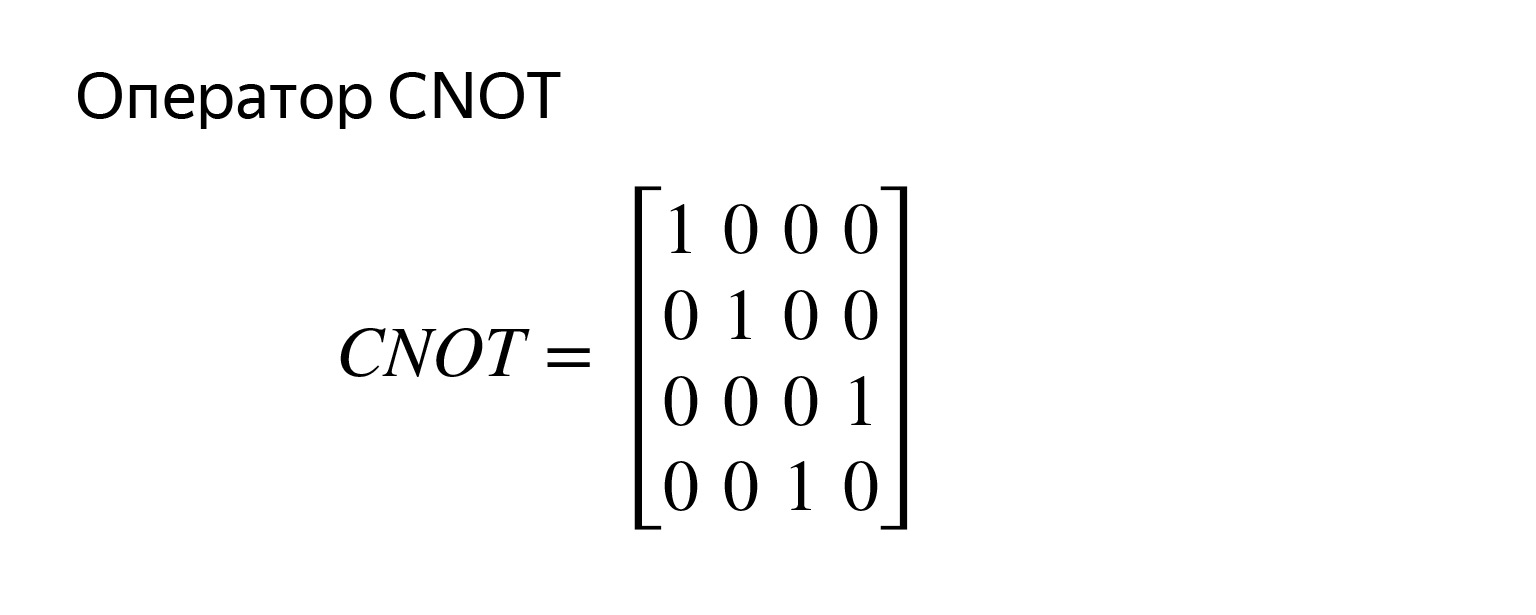
矩阵已经是四乘四了。对于两个量子比特,看起来像这样。我将把这个问题留在星号上,以进行乘法运算,看看这是否正确。

这个东西甚至可以被编程。没有火箭科学。您只需要创建一个包含两个量子位和两个经典量子位的电路,然后不仅执行CNOT,还执行CX受控否定。
否定是X运算符,因此原则上一切都是合乎逻辑的。您可以绘制一个图表。该方案如下。
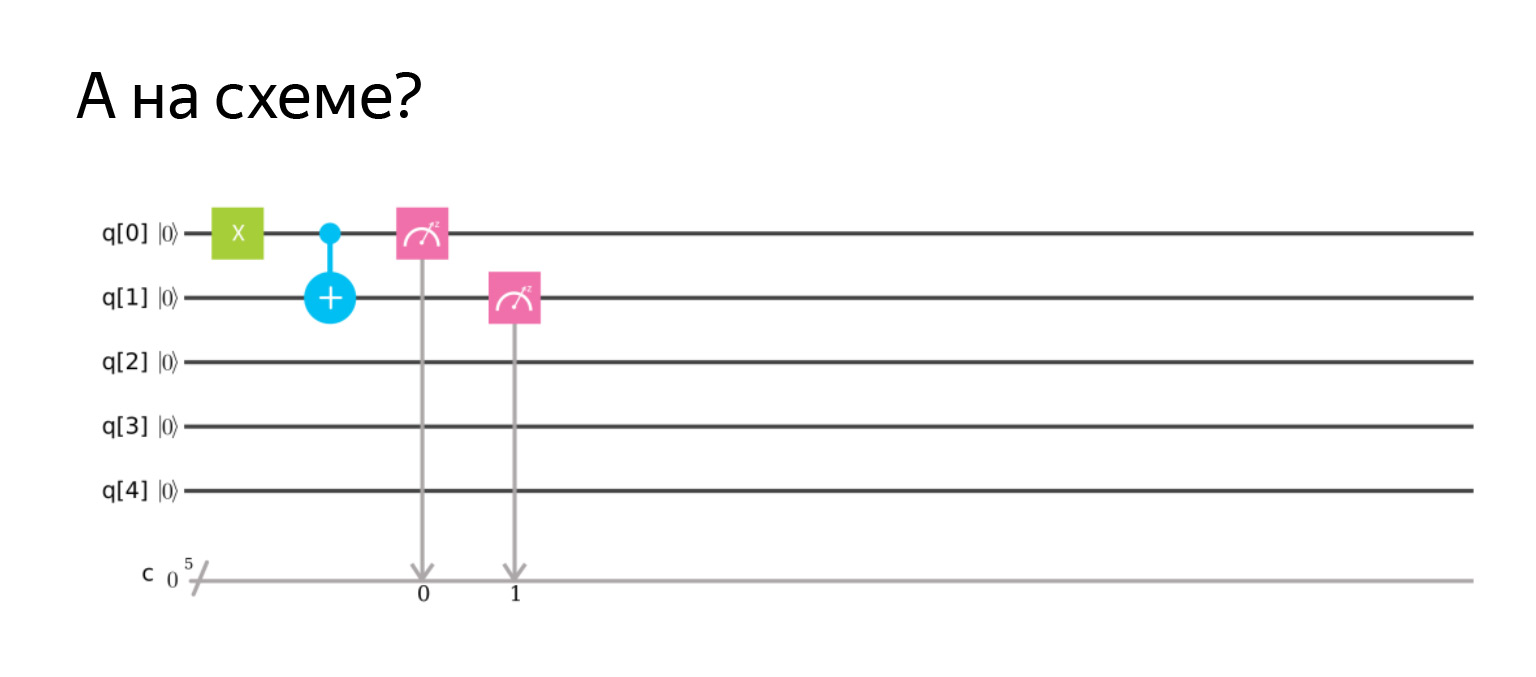
也就是说,受控否定是我们要更改的量子位上的一个加号。关键是控制。在这里,如果量子位是统一的,那么我们将更改第二个。

在这里,我首先专门反转第一个,使其为1,然后对二者进行测量并得出结果|11⟩。一切都如我们所料。
但是现在是时候一起使用我们所有的知识了。

让我们采用我们所知道的所有三个或四个运算符,并将它们放入一个方案中。也就是说,我们将Hadamard运算符应用于第一个运算符。倒转第二个,然后加在一起,进行受控的取反和测量。
让我们暂不运行它,但是尝试猜测会发生什么。
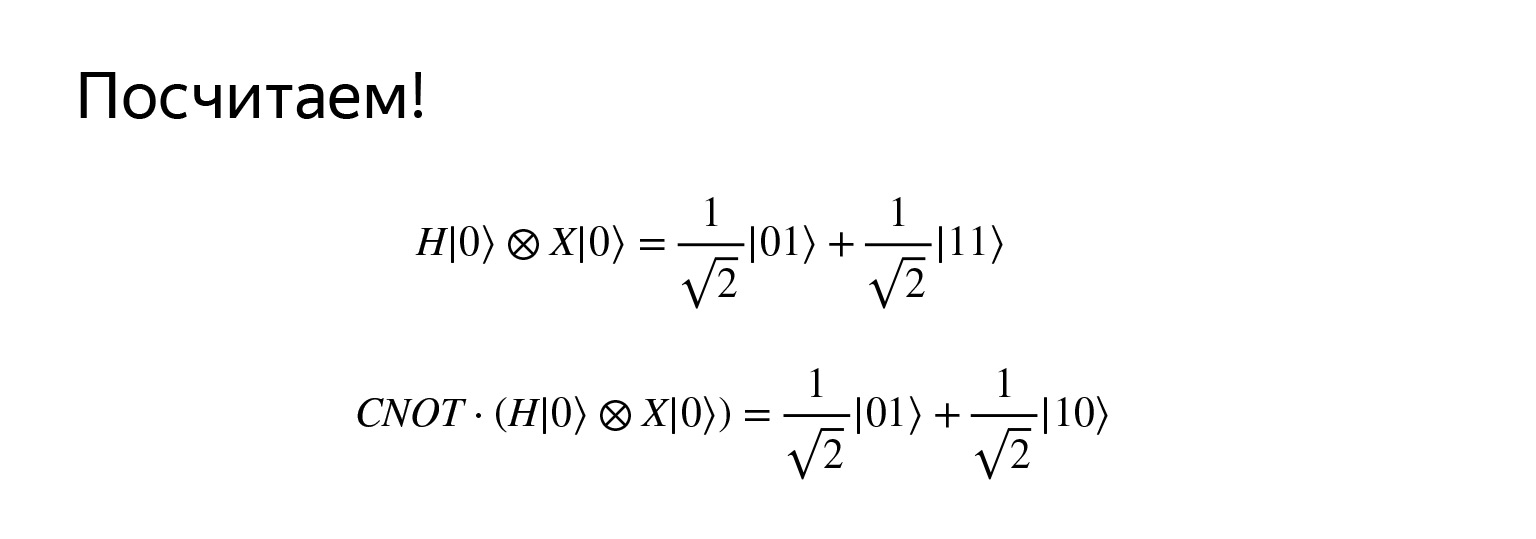
如果我们将Hadamard运算符应用于第一个量子位,然后对第二个量子位求反,则得到这样的叠加。我不想现在浪费时间进行检查,它可以很容易地成倍增加。但是这个职位很有趣。首先,它与统一非常相似,其次,如果我们也进行受控否定,则此状态称为纠缠。

状态令人困惑。又为什么呢让我们尝试进行测量。看,如果我测量第一个量子位并且它处于零状态,那么我可以说第二个量子位一定处于状态一。
也就是说,如果我用我的量子位进行这样的转换,我给我的朋友一个量子位,他将飞往纽约,然后我自己测量第二个量子位,我将确切知道他的量子位处于什么状态。这称为量子纠缠或量子连接性的影响。这是量子计算工作的主要机制。它将改变,它们的连接非常牢固,在测量过程中,我们只能得到|00⟩或|11⟩。
在这种情况下,有一个非常有趣的例证,我认为

分心的是他一直都穿着不同的袜子。他的同事开玩笑说:如果他用一只脚进入房间,我们看到袜子是粉红色的,那么我们可以肯定地说第二只袜子不是粉红色的。这样吧。
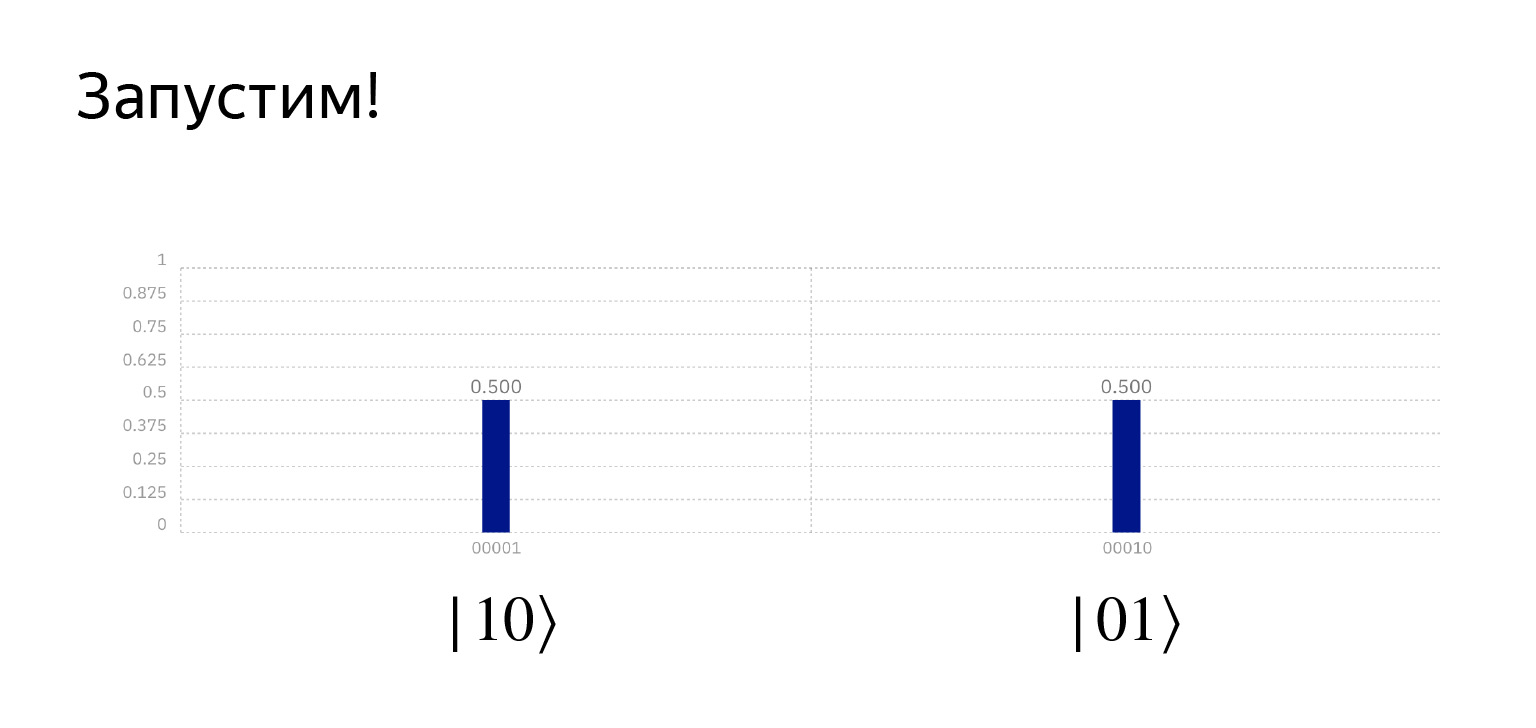
如果我们运行这个程序,我们将得到我们想要的。这里已经很有趣了。机率正好是0.5,但这是一个巧合。
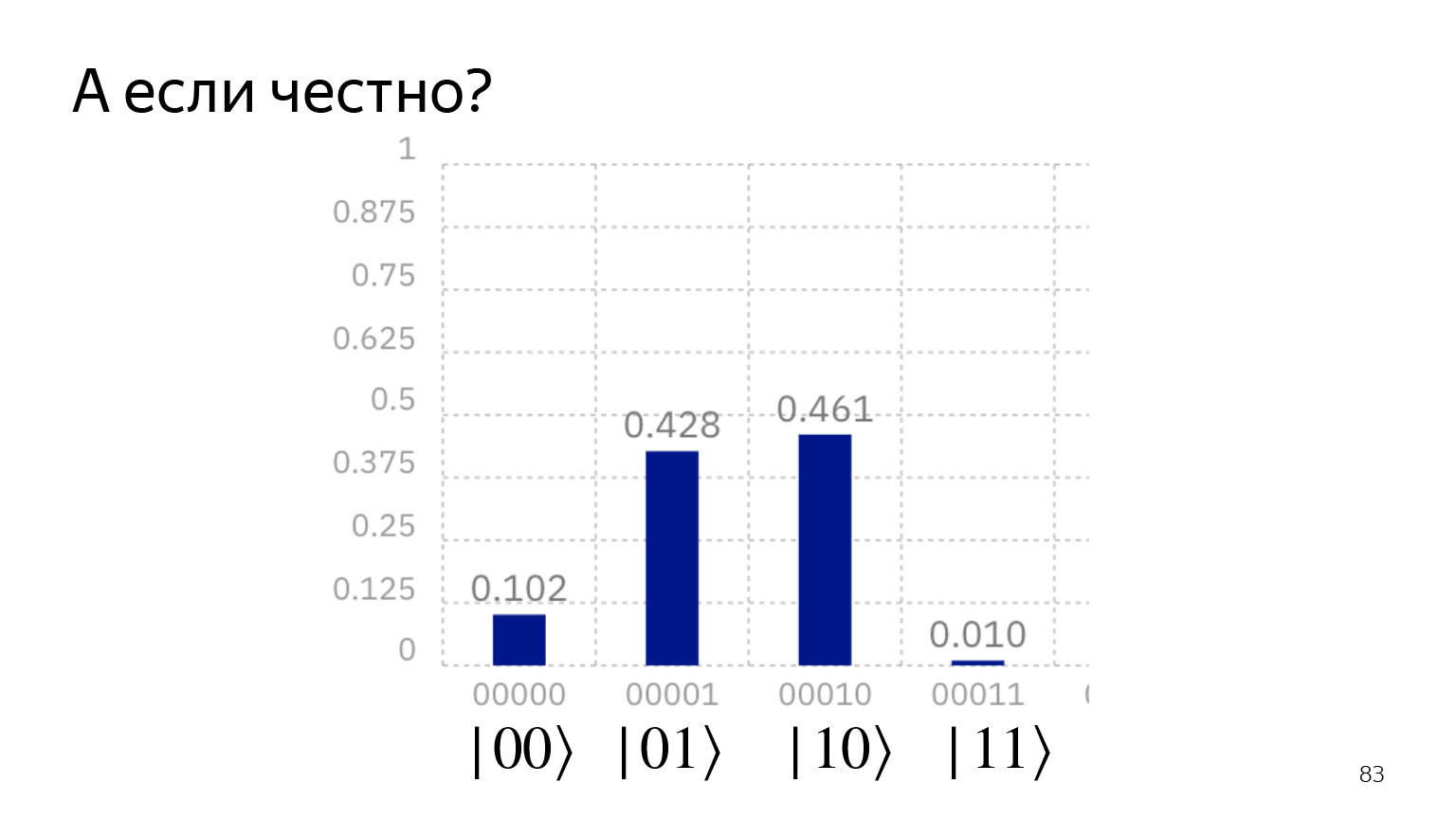
如果我们诚实地在量子计算机上运行,我们将得到这张照片。我们似乎在说:永远无法获得状态|00⟩,而永远无法获得状态|11⟩。但是它仍然有效:当前的技术状态使得存在无法始终被轻易抑制的噪声。他们为此而苦苦挣扎。
但是,如果您还记得古典计算机科学,那是同一回事:纠错代码以及所有这些。只是qubit太小了,无法在纠错上花费额外的位。
现在,正如我所承诺的,一些算法示例。但是这些只是没有根据的算法分析而没有根据的示例,因此您看起来,认为变得感兴趣。

第一种算法与Deutsch有关,我们一开始就谈到过。这是Deutsch-Jozy算法。并且他执行以下操作。假设我们在n个变量中有一个布尔函数。我们肯定知道它是恒定的还是平衡的。平衡意味着在参数的正好一半上它等于零,而在另一半上则等于1。让我们尝试经典地检查它是否恒定。
为此,我们至少需要检查所有可能选项的一半:2 n – 1 +1选项。量子算法允许您在对函数本身进行n次计算的n次调用中进行此操作。命中次数成倍降低。
第二个示例可能是每个人都熟知的,因为它说量子计算机将破坏所有密码学:我们可以非常快速地分解数字量子。

这里给出了困难的估计,并且有一个很好的例子。在2011年,数字15是在真实计算机上计算的,花了7个量子比特。

但是,并非一切都那么糟糕。如果量子计算机达到可以破坏RSA的水平,那么已经有后量子密码学了。它建立在有错误的学习之上。这是将小错误引入到问题中的时候,因此很难找到答案。通常,这些是某种方程或方程组。这是算法的示例。任何想要阅读的人都可以阅读更多详细信息。
最有趣的是:新希望算法就是基于这个东西,全人类的新希望。 Chrome在2016年增加了对此算法的支持。这里有博客链接。这不是我的主意,实际上一切都是如此。未来已经来临。
最后有一些链接:
- , : Michael A.Nielsen and Isaac L. Chuang, «Quantum Computation and Quantum Information». , . .
- IBM Q: quantumexperience.ng.bluemix.net
- IBM Q User Guide: quantumexperience.ng.bluemix.net/proxy/tutorial/full-user-guide/introduction.html
- Qiskit: qiskit.org
- :
nplus1.ru/material/2017/06/07/quantumcomputers
nplus1.ru/news/2017/05/26/quantum-blockchain
这或多或少都是。我只想补充一下,大约50年前,当Deutsch开始进行量子信息科学时,计算机很大。它们是由几家公司制造的。它们大约是衣柜的大小。现在,几乎相同的公司生产大型量子计算机。而且,当然,我们不知道50年后会发生什么。
如果您尝试输入自己喜欢的搜索引擎,那么今天您可以找到量子程序员的职位空缺。当然,还有更多的研究。谢谢。