
我必须马上说:我不是IT专家,而是统计领域的爱好者。另外,这些年来,我参加了各种一级方程式预测比赛。因此,我的模型所面临的任务是:发布不比“目测”创建的预测更糟糕的预测。理想情况下,该模型当然应该击败人类对手。
该模型仅专注于预测资格的结果,因为资格比种族更容易预测并且更容易建模。但是,当然,将来我计划创建一个模型,该模型可以足够准确地预测比赛的结果。
为了创建一个模型,我在一张表中总结了2018和2019赛季的所有实践和资格证书结果.2018年作为训练样本,2019年作为测试样本。根据这些数据,我们建立了线性回归。为了使回归尽可能简单,我们的数据是坐标平面上的点的集合。我们绘制的直线与这些点的总和最小。函数,其图形为这条线-这是我们的线性回归。
根据学校课程中已知的公式我们的功能仅以我们有两个变量这一事实为特色。第一个变量(X1)是第三次练习中的滞后,第二个变量(X2)是先前资格中的平均滞后。这些变量不是等效的,我们的目标之一是确定每个变量的权重在0到1范围内。变量从0开始越远,在解释因变量时就越重要。在我们的案例中,因变量是圈速,表示为领先于领导者的滞后时间(或更确切地说,来自某个“理想圈”),因为该值对所有飞行员都是正值。
《 Moneyball》一书的爱好者(电影中没有对此进行解释)可能还记得,通过线性回归,他们确定基准百分比(又称为OBP)(基准百分比)与所获得的伤口比其他统计数据更紧密相关。我们的目标大致相同:了解哪些因素与学历成绩最相关。回归的一大优势在于它不需要高级的数学知识:我们只需输入数据,然后Excel或其他电子表格编辑器即可为我们提供现成的系数。
基本上,我们想了解线性回归的两件事。首先,我们选择的自变量在多大程度上解释了功能的变化。其次,这些独立变量的重要性。换句话说,更能解释资格赛结果的是:先前赛道的比赛结果或同一赛道的训练结果。
这里要注意一个重点。最终结果是两个独立参数的总和,每个参数均来自两个独立的回归。第一个参数是团队在现阶段的实力,更确切地说,是团队最好的飞行员与领导者之间的差距。第二个参数是团队内部的力量分布。
以身作则意味着什么?假设我们参加了2019匈牙利大奖赛。该模型显示,法拉利将落后领先者0.218秒。但这是第一位飞行员的滞后,他们将是谁-维特尔或莱克莱尔-他们之间的差距将由另一个参数决定。在此示例中,模型显示维特尔将领先,莱克莱尔将因此而损失0.096秒。
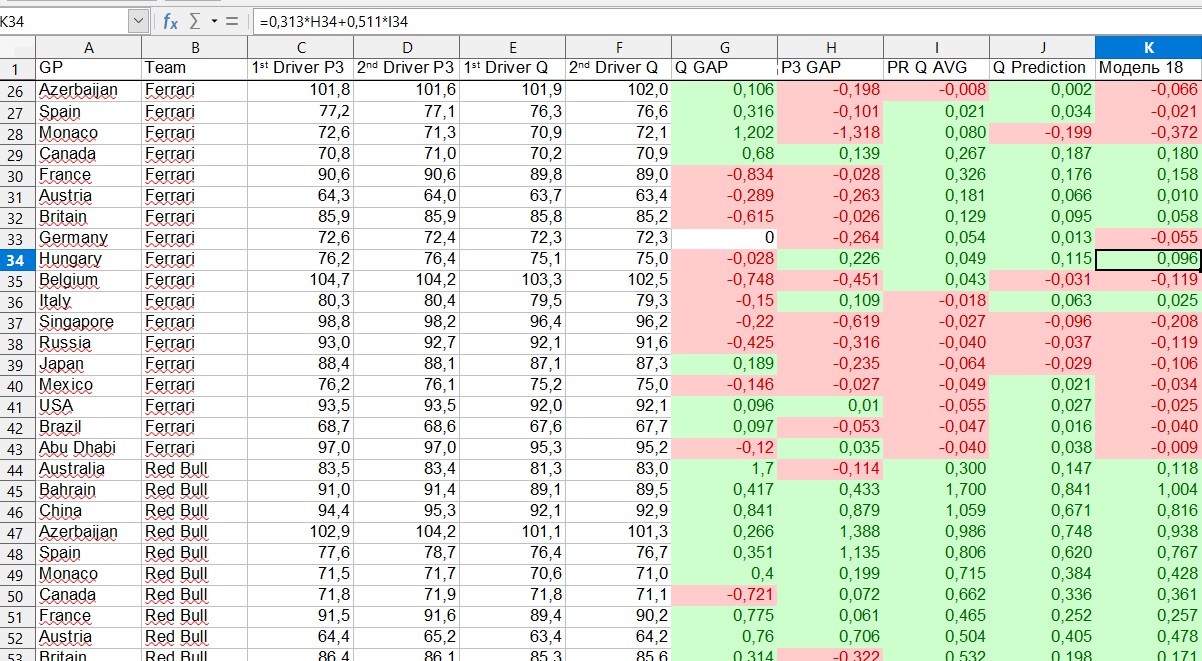
为什么会有这样的困难?单独考虑每个飞行员,而不是分解成团队落后和第一位飞行员与团队中第二位飞行员的滞后,难道不是更容易吗?也许是这样,但是我的个人观察表明,查看团队的结果比查看每个飞行员的结果要可靠得多。一名飞行员可能会犯错,或者飞离跑道,或者他会遇到技术问题-这一切都会给模型带来混乱,除非您手动跟踪每种不可抗力情况,这会花费太多时间。不可抗力对团队成绩的影响要小得多。
但是回到我们想要评估我们选择的解释变量解释功能变化的程度。这可以使用确定系数来完成。它将显示实习结果和以前的资格证书对资格证书结果的解释程度。
由于我们建立了两个回归,因此我们也有两个确定系数。第一个回归负责阶段的团队水平,第二个回归负责同一团队的飞行员之间的对抗。在第一种情况下,确定系数为0.82,也就是说,资格条件的82%由我们选择的因素解释,另外18%-由我们未考虑的其他因素解释。这是一个很好的结果。在第二种情况下,确定系数为0.13。
从本质上讲,这些指标意味着该模型可以很好地预测团队水平,但是很难确定队友之间的差距。但是,对于最终目标,我们不需要知道差距,我们只需要知道两个飞行员中的哪个更高,模型就可以解决这个问题。在62%的情况下,该模型的排名高于实际资格较高的飞行员。
同时,在评估团队实力时,上一次培训的结果比以前的资格要重要一倍半,但在团队内部对决中则相反。这一趋势在2018年和2019年的数据中均得到体现。
最终公式如下:
第一个试点:
第二飞行员:
让我提醒您,X1是第三次练习中的滞后,X2是先前资格中的平均滞后。
这些数字是什么意思。他们的意思是团队的资格水平由第三次练习的结果确定为60%,由先前阶段的资格证书的结果确定为40%。因此,第三次练习的结果是以前资格考试结果的重要因素大一倍半。
一级方程式赛车的粉丝可能知道这个问题的答案,但是对于其余的赛车,您应该评论一下我为什么接受第三次练习的结果。一级方程式有三种做法。但是,团队通常是在后者中训练资格证书。但是,如果第三种做法由于下雨或其他不可抗力而失败,我将采用第二种做法的结果。据我所记得,在2019年只有一个这样的情况-在日本大奖赛上,由于台风,舞台以缩短的形式举行。
另外,可能有人注意到该模型使用先前资格中的平均滞后时间。但是,本赛季的第一阶段呢?我使用了前一年的滞后,但并没有保留它们,而是根据常识对其进行了手动调整。例如,在2019年,法拉利平均比红牛快0.3秒。但是,看来意大利队今年将没有这种优势,或者他们将完全落后。因此,在2020赛季的第一阶段,即奥地利大奖赛上,我手动将红牛带到了法拉利。
这样,我得到了每个飞行员的滞后,按滞后对飞行员进行排名,并获得了最终的资格预测。但是,重要的是要了解第一和第二个飞行员是纯粹的惯例。回到匈牙利大奖赛的维特尔和莱克莱尔的例子中,该模型认为塞巴斯蒂安是第一位飞行员,但在许多其他阶段,她更喜欢莱克莱尔。
结果
就像我说的,任务是创建一个模型,使人们能够进行预测。作为基础,我采用了“预测”和“队友的预测”,这些预测是“通过眼睛”创建的,但要仔细研究实践的结果并进行联合讨论。
评分系统如下。仅考虑了前十名飞行员。对于准确的命中,预测获得9分,位置1的未命中6点,位置2的未命中4点,位置3的未命中2点,以及位置4的未命中1点。也就是说,如果飞行员在预测中排名第三,因此他获得了杆位,则预测得到4分。
使用此系统,21项大奖赛的最高积分是1890.
人类参与者分别获得1056、1048和1034积分。
该模型获得了1031分,尽管在系数的轻度操纵下,我也获得了1045和1053分。
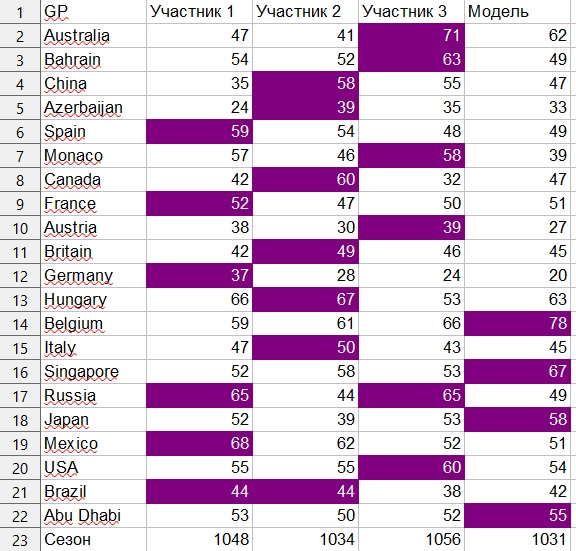
就我个人而言,我对结果感到满意,因为这是我建立回归的初次经验,它带来了相当令人满意的结果。当然,我想对它们进行改进,因为我敢肯定,借助构建模型的帮助,即使是像这样简单的模型,也可以取得比仅凭眼图评估数据更好的结果。例如,在此模型的框架内,有可能考虑到一些团队在实践中表现较弱但在资格方面“得分高”的因素。例如,有观察表明,梅赛德斯在训练期间通常不是最好的球队,但在资格方面表现要好得多。但是,这些人类观察结果并未反映在模型中。因此,在从7月开始的2020赛季(如果没有意外发生的话),我想在与实时天气预报员的比赛中测试该模型,并发现,如何使其变得更好。
此外,我希望引起一级方程式赛车迷的共鸣,并相信通过交流思想,我们可以更好地理解什么是资格赛和比赛的结果,这最终是任何做出预测的人的目标。