其中q是粒子的电荷,r ij是粒子之间的距离,C是一些常数,具体取决于测量单位的选择。在SI中-在SGS-1中,在我的程序中(其中能量以电子伏特表示,距离以埃表示,电荷以基本电荷表示)C大约等于14.3996。
那你说什么呢?只需将相应的项添加到线对电位中即可。但是,在MD建模中,最常见的情况是使用周期性边界条件,即模拟系统从四面八方包围着无限数量的虚拟副本。在这种情况下,我们系统的每个虚拟图像将根据库仑定律与系统内部的所有带电粒子相互作用。而且,由于库仑相互作用随距离(如1 / r)的减小非常微弱,因此消除它并不是那么容易,这意味着我们无法根据这样的距离进行计算。一系列形式的1 / x发散,即原则上,其数量可以无限期增长。现在,你不给一碗汤加盐吗?用电会杀死你吗?
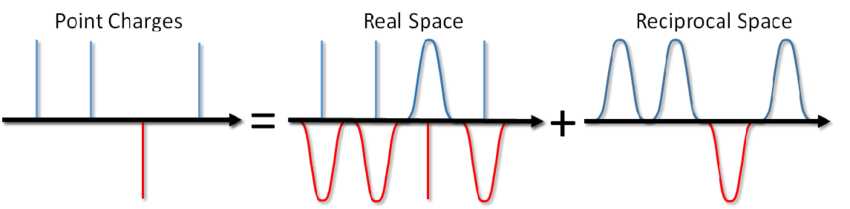
...您不仅可以给汤加盐,还可以计算周期性边界条件下库仑相互作用的能量。此方法由Ewald 于1921年提出,用于计算离子晶体的能量(您也可以在Wikipedia上看到它)。该方法的本质是屏蔽点电荷,然后减去屏蔽功能。在这种情况下,静电相互作用的一部分被减少为短效相互作用,并且可以简单地以标准方式将其切断。剩余的远程部分有效地在傅立叶空间中求和。忽略结论,可以在Blinov的文章中或Frenkel和Smith的同一本书中查看该结论,我将立即写下一个称为Ewald sum的解决方案:
其中α是一个参数,用于调节前向和后向空间中的计算比率,k是在进行求和的倒数空间中的向量,V是系统的体积(前向空间)。第一部分(E real)是短距离的,并且是在与其他对电势相同的周期中计算的,请参阅上一篇文章中的real_ewald函数。最后的贡献(Eonst)是对自相互作用的校正,通常被称为“常数部分”,因为它不依赖于粒子的坐标。它的计算是微不足道的,因此我们只关注Ewald和(E rec),在对等空间中求和。自然,在Ewald推导之时,没有分子动力学;我找不到谁最早在MD中使用此方法。现在,任何有关MD的书都将其介绍作为一种黄金标准。要预订,Allen甚至在Fortran中提供了示例代码。幸运的是,我仍然拥有曾经用C编写的用于顺序版本的代码,它仅用于并行化(我允许自己省略一些变量声明和其他无关紧要的细节):
void ewald_rec()
{
int mmin = 0;
int nmin = 1;
// iexp(x[i] * kx[l]),
double** elc;
double** els;
//... iexp(y[i] * ky[m])
double** emc;
double** ems;
//... iexp(z[i] * kz[n]),
double** enc;
double** ens;
// iexp(x*kx)*iexp(y*ky)
double* lmc;
double* lms;
// q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
double* ckc;
double* cks;
//
eng = 0.0;
for (i = 0; i < Nat; i++) //
{
// emc/s[i][0] enc/s[i][0]
// elc/s , .
elc[i][0] = 1.0;
els[i][0] = 0.0;
// iexp(kr)
sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
}
// emc/s[i][l] = iexp(y[i]*ky[l]) ,
for (l = 2; l < ky; l++)
for (i = 0; i < Nat; i++)
{
emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
}
// enc/s[i][l] = iexp(z[i]*kz[l]) ,
for (l = 2; l < kz; l++)
for (i = 0; i < Nat; i++)
{
enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
}
// K-:
for (l = 0; l < kx; l++)
{
rkx = l * twopi * ra;
// exp(ikx[l]) ikx[0]
if (l == 1)
for (i = 0; i < Nat; i++)
{
elc[i][0] = elc[i][1];
els[i][0] = els[i][1];
}
else if (l > 1)
for (i = 0; i < Nat; i++)
{
// iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
x = elc[i][0];
elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
}
for (m = mmin; m < ky; m++)
{
rky = m * twopi * rb;
// iexp(kx*x[i]) * iexp(ky*y[i])
if (m >= 0)
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
}
else // m :
for (i = 0; i < Nat; i++)
{
lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
}
for (n = nmin; n < kz; n++)
{
rkz = n * twopi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < rkcut2) //
{
// (q[i]*iexp(kr[k]*r[i])) -
sumC = 0; sumS = 0;
if (n >= 0)
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);
sumC += ckc[i];
sumS += cks[i];
}
else // :
for (i = 0; i < Nat; i++)
{
//
ch = charges[types[i]].charge;
ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);
sumC += ckc[i];
sumS += cks[i];
}
//
akk = exp(rk2 * elec->mr4a2) / rk2;
eng += akk * (sumC * sumC + sumS * sumS);
for (i = 0; i < Nat; i++)
{
x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
fxs[i] += rkx * x;
fys[i] += rky * x;
fzs[i] += rkz * x;
}
}
} // end n-loop (over kz-vectors)
nmin = 1 - kz;
} // end m-loop (over ky-vectors)
mmin = 1 - ky;
} // end l-loop (over kx-vectors)
engElec2 = eng * * twopi * rvol;
}
对代码的一些解释:函数针对所有k矢量和所有粒子,从k向量的矢量乘积和粒子的半径矢量计算复数指数(在代码注释中表示为iexp以从括号中除去虚部)。该指数乘以粒子电荷。接下来,计算所有粒子的此类乘积的总和(E rec公式中的内部总和),以弗伦克尔为单位的电荷密度,以布利诺夫为单位的结构因数。然后,基于这些结构因素,计算作用在粒子上的能量和力。 k矢量的分量(2π* l / a,2π* m / b,2π* n / c)的特征在于三个整数l,m和n,该操作将循环运行,直至达到用户指定的限制。参数a,b和c分别是模拟系统的尺寸x,y和z(对于具有长方体几何形状的系统而言,结论是正确的)。在代码中,1 / a,1 / b和1 / c对应于变量ra,rb和rc。每个值的数组有两个副本:实部和虚部。通过将前一个乘以1进行复数运算,可以从前一个乘积迭代地获得一个维中的每个下一个k矢量,以免每次都不计算余弦的正弦值。为所有m填充emc / s和enc / s数组和Ñ,分别与所述阵列ELC / s的地方为每个值升在零指数> 1 升,以节省存储器。
出于并行化的目的,有利的是“反转”循环的顺序,以便外部循环在粒子上运行。在这里,我们看到一个问题-该函数只能在计算所有粒子的总和(电荷密度)之前并行化。进一步的计算基于该数量,并且仅在所有线程完成工作后才进行计算,因此您必须将此函数分为两个。第一个计算电荷密度,第二个计算能量和力。请注意,第二个函数将再次需要数量q i在上一步中计算的每个粒子和每个k向量的iexp(kr)。这里有两种方法:要么重新计算它,要么记住它。
第一个选项需要更多的时间,第二个选项需要更多的内存(粒子数* k矢量数* sizeof(float2))。我选择了第二个选项:
__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
int i; // for atom loop
int ik; // index of k-vector
int l, m, n;
int mmin = 0;
int nmin = 1;
float tmp, ch;
float rkx, rky, rkz, rk2; // component of rk-vectors
int nkx = md->nk.x;
int nky = md->nk.y;
int nkz = md->nk.z;
// arrays for keeping iexp(k*r) Re and Im part
float2 el[2];
float2 em[NKVEC_MX];
float2 en[NKVEC_MX];
float2 sums[NTOTKVEC]; // summ (q iexp (k*r)) for each k
extern __shared__ float2 sh_sums[]; // the same in shared memory
float2 lm; // temp var for keeping el*em
float2 ck; // temp var for keeping q * el * em * en (q iexp (kr))
// invert length of box cell
float ra = md->revLeng.x;
float rb = md->revLeng.y;
float rc = md->revLeng.z;
if (threadIdx.x == 0)
for (i = 0; i < md->nKvec; i++)
sh_sums[i] = make_float2(0.0f, 0.0f);
__syncthreads();
for (i = 0; i < md->nKvec; i++)
sums[i] = make_float2(0.0f, 0.0f);
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
ik = 0;
for (i = id0; i < N; i++)
{
// save charge
ch = md->specs[md->types[i]].charge;
el[0] = make_float2(1.0f, 0.0f); // .x - real part (or cos) .y - imagine part (or sin)
em[0] = make_float2(1.0f, 0.0f);
en[0] = make_float2(1.0f, 0.0f);
// iexp (ikr)
sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));
// fil exp(iky) array by complex multiplication
for (l = 2; l < nky; l++)
{
em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
}
// fil exp(ikz) array by complex multiplication
for (l = 2; l < nkz; l++)
{
en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
}
// MAIN LOOP OVER K-VECTORS:
for (l = 0; l < nkx; l++)
{
rkx = l * d_2pi * ra;
// move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
if (l == 1)
el[0] = el[1];
else if (l > 1)
{
// exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
tmp = el[0].x;
el[0].x = tmp * el[1].x - el[0].y * el[1].y;
el[0].y = el[0].y * el[1].x + tmp * el[1].y;
}
//ky - loop:
for (m = mmin; m < nky; m++)
{
rky = m * d_2pi * rb;
//set temporary variable lm = e^ikx * e^iky
if (m >= 0)
{
lm.x = el[0].x * em[m].x - el[0].y * em[m].y;
lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
}
else // for negative ky give complex adjustment to positive ky:
{
lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
}
//kz - loop:
for (n = nmin; n < nkz; n++)
{
rkz = n * d_2pi * rc;
rk2 = rkx * rkx + rky * rky + rkz * rkz;
if (rk2 < md->rKcut2) // cutoff
{
// calculate summ[q iexp(kr)] (local part)
if (n >= 0)
{
ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
}
else // for negative kz give complex adjustment to positive kz:
{
ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
}
sums[ik].x += ck.x;
sums[ik].y += ck.y;
// save qiexp(kr) for each k for each atom:
md->qiexp[i][ik] = ck;
ik++;
}
} // end n-loop (over kz-vectors)
nmin = 1 - nkz;
} // end m-loop (over ky-vectors)
mmin = 1 - nky;
} // end l-loop (over kx-vectors)
} // end loop by atoms
// save sum into shared memory
for (i = 0; i < md->nKvec; i++)
{
atomicAdd(&(sh_sums[i].x), sums[i].x);
atomicAdd(&(sh_sums[i].y), sums[i].y);
}
__syncthreads();
//...and to global
int step = ceil((double)md->nKvec / (double)blockDim.x);
id0 = threadIdx.x * step;
N = min(id0 + step, md->nKvec);
for (i = id0; i < N; i++)
{
atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
}
}
// end 'ewald_rec' function
__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
int i; // for atom loop
int ik; // index of k-vector
float tmp;
// accumulator for force components
float3 force;
// constant factors for energy and force
float eScale = md->ewEscale;
float fScale = md->ewFscale;
int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
int N = min(id0 + atPerThread, md->nAt);
for (i = id0; i < N; i++)
{
force = make_float3(0.0f, 0.0f, 0.0f);
// summ by k-vectors
for (ik = 0; ik < md->nKvec; ik++)
{
tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);
force.x += tmp * md->rk[ik].x;
force.y += tmp * md->rk[ik].y;
force.z += tmp * md->rk[ik].z;
}
md->frs[i].x += force.x;
md->frs[i].y += force.y;
md->frs[i].z += force.z;
} // end loop by atoms
// one block calculate energy
if (blockIdx.x == 0)
if (threadIdx.x == 0)
{
for (ik = 0; ik < md->nKvec; ik++)
md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
}
}
// end 'ewald_force' function
希望您能原谅我用英语发表评论,代码实际上与串行版本相同。由于数组丢失了一个维度,因此代码甚至变得更具可读性:elc / s [i] [l],emc / s [i] [m]和enc / s [i] [n]变成一维el,em和en,将数组lmc / s和ckc / s-放入变量lm和ck(粒子的大小消失了,因为不再需要为每个粒子存储它,中间结果被累积在共享内存中)。不幸的是,一个问题立即出现:数组em和en必须将其设置为静态,以便不使用全局内存并且每次都不动态分配内存。其中的元素数量由NKVEC_MX指令(在一维中k个向量的最大数量)确定,并且在运行时仅使用第一个nky / z元素。另外,出现了所有k个向量的端到端索引和类似的伪指令,从而限制了这些向量NTOTKVEC的总数。如果用户需要比指令指定的k向量更多的k向量,则会出现问题。为了计算能量,提供了一个索引为零的块,因为哪个块以何种顺序执行此计算并不重要。请注意,在变量akk中计算的值串行代码仅取决于仿真系统的大小,并且可以在初始化阶段进行计算,在我的实现中,它存储在每个k矢量的md-> exprk2 []数组中。类似地,k矢量的分量来自md-> rk []数组。由于该方法基于该方法,因此可能有必要使用现成的FFT函数,但是我仍然没有弄清楚该如何做。
好吧,现在让我们尝试计算一下,但相同的氯化钠。让我们摄取2000个钠离子和等量的氯。让我们设置的收费为整数,并采取对势,例如,从这项工作... 让我们随机设置启动配置,并将其稍微混合,图2a。我们选择系统的体积,使其对应于室温下氯化钠的密度(2.165 g / cm 3)。让我们在短时间内(5飞秒的10,000步,5飞秒)开始所有这些操作,根据库仑定律并使用Ewald求和,天真地考虑静电。最终的配置分别显示在图2b和2c中。似乎在埃瓦尔德(Ewald)的情况下,该系统比没有他的情况下更为简化。同样重要的是,总和的波动随着求和的使用而显着减少。

图2. NaCl系统的初始配置(a)和10,000积分步骤之后:以一种简单的方式(b)和使用Ewald方案(c)。
而不是结论
注意,图中获得的结构并不对应于NaCl晶格,而是对应于ZnS晶格,但这已经成为对电势的抱怨。考虑到静电对于分子动力学建模非常重要。可以认为,静电相互作用是导致晶格形成的原因,因为它的作用距离很长。的确,从这个位置很难解释冷却过程中氩气等物质如何结晶。
除了提到的Ewald方法外,还有其他解决静电的方法,例如,参见本评论。