
在绝大多数情况下,业务优化与线性规划方法的使用有关。该方法非常简单。另外,关于解的存在性和唯一性有一个定理。
但是,实际上,并非所有事情都完全简单。
第一个问题是现实世界条件的非线性。为了使线性编程方法适用,必须将它们线性化。有一些方法可以通过引入新变量,设置权重系数等来通过线性方程和不等式合理地设置非线性。在这种情况下解决生产问题时,必须使用大量变量进行操作,并因此需要使用方程式(不等式)。
在解决极值问题的理论中,关于线性规划问题的解的稳定性有一个定理。据此,只有问题的范围是凸的,解决方案才是稳定的。由于存在大量变量和不等式,因此无法确定问题的范围是否是凸的。而且,不凸的可能性很高。
如果问题不稳定,则取决于遍历顶点的起点,将获得不同的结果。
第二个问题-从下方开始变量限制(x> h> 0)。线性编程方法的任何实现都将始终提供非零的x值。如果x恰好等于h,则意味着变量x的值应实质上为零。实际上,这种“虚拟”体积(方法峰度)分散在“有意义”变量上。这种做法的结果是侵蚀了最佳解决方案的概念,如果这种解决方案是决策链中众多解决方案之一,则尤为重要。
第三个问题是管理。线性编程方法仅给出一个结果。以及如何看待接近最佳的结果?例如,在最终的解决方案中,供应商评级很差。如何了解是否有紧密的解决方案,但是要寻找可靠的供应商。
运输任务
该示例对应于运输线性规划问题。
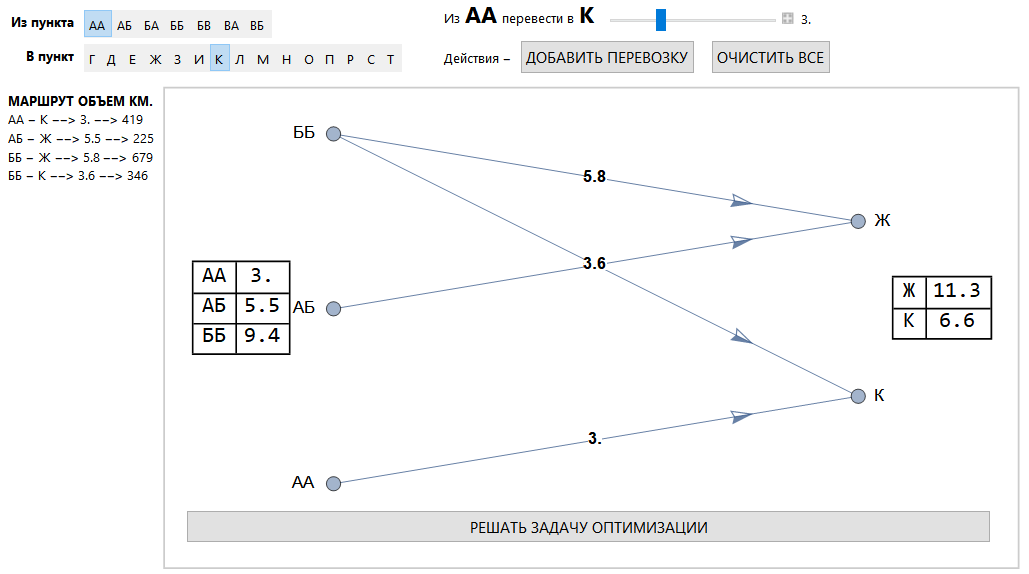
有5个运输公司(任务是煤炭运输),其中有两个关税计算。关税边界和关税本身可以更改(它们是参数设置的)。

运输指定为点对点(根据公认的煤炭运输方法)和运输量。
接口的一般视图。

运输分配区。
集群解法
解决了一系列问题,而不是一个线性规划问题,其数量对应于关税的所有可能组合。在以上发货中,有127个(第二个值在左上角的矩形中)。

从剩下的正确问题中选择最佳解决方案。每个任务都为关税的特定组合提供了最佳解决方案。上述解决方案构成了最大值的某个范围。
为什么聚类方法好:
- 对解决方案的稳定性有所了解。
- 从下方限制的变量没有“虚拟”体积,因为将存在另一种不存在这种条件的组合(因为不存在这种变量)。
- 可以使用标准线性规划方法引入主观条件(评分,偏好)。
随着装运数量的增加,我们有以下图片(片段)。
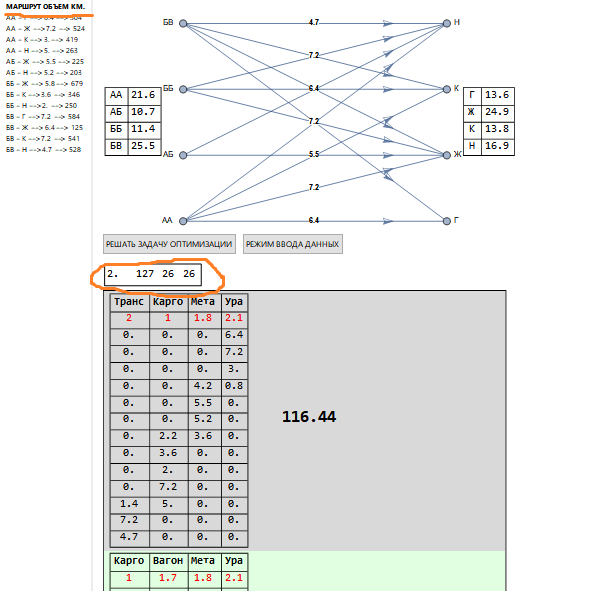
在解决方案上方的矩形(橙色突出显示)的左上角中,指示了除以前以外的其他值:127-组合(与关税表的结构有关,如前所述),26-对应于要解决的正确问题的数量。所使用的费率在承运人的名称下以红色指示,运输栏对应于路线列表(橙色下划线)。
重要的是要注意,所使用的方法可以让您了解结果,评估类似的解决方案并在选择替代方案时利用您的专业经验,同时要考虑到经营特定业务的复杂性。