厌倦了检疫工作的约书亚·格林(Joshua Green)和安德鲁·洛布(Andrew Lobb)想出了如何证明矩形钉定理的变体之一

可以在闭环中找到各种矩形吗?
3月中旬,数学家约书亚·格林(Joshua Green)和安德鲁·洛布(Andrew Lobb)发现自己处于相似的位置-锁在四堵墙内,试图适应日趋严重的冠状病毒流行。他们决定通过研究来解决这个问题。
波士顿学院的教授格林说:“我认为大流行是这一过程的某种催化剂。”他说:“我们认为最好进行某种可以支持我们的联合工作。”
这两个朋友决定解决的问题之一是几何问题的一种变体,至今仍未解决一百年。
“这项任务的制定和理解非常简单,但很难解决,”-说华盛顿和李大学的伊丽莎白·丹恩。
一切都始于闭环-任何具有相同起点和终点的弯曲路径。Green和Lobb承担的任务实质上是,在任何这样的路径中,都有四个点组成的集合,这些点构成了任何给定比例的矩形的顶点。
尽管这个“矩形钉子问题”听起来像是任何有尺子和指南针的高中生都可以解决的问题,但数十年来,他抵制了数学家最持久的尝试。当格林和洛伯接任时,他们没有理由期待其他事情。
格林说,在他从事的所有困难项目中,“在我看来,这是最没有希望的项目。”
但是这种流行病愈演愈烈,分别在英国达勒姆大学和冲绳科技学院工作的格林和洛伯每周进行一次Zoom对话,并迅速产生了一些想法。然后在5月19日,世界许多地方重新开放时,他们发表了决定。
他们的最终证明表明确实可以找到矩形,将这个问题带到了完全不同的几何层次。在这里,这个顽固的问题很容易解决。布朗大学的理查德·施瓦茨
说:“这很奇怪。” “这个想法非常适合完成这项任务。”
重新思考矩形
矩形钉的问题与德国数学家奥托·特普利茨(OttoTöplitz)在1911年提出的问题密切相关。他预测,在任何闭合曲线上都可以找到四个点,将它们连接起来可以得到一个正方形。他关于“方钉”的问题仍然悬而未决。
格林说:“这是一项古老而令人沮丧的任务,不能以任何方式破解。”
要了解问题的复杂性,重要的是要知道平方钉问题中考虑的曲线的特性-这对于证明Green和Lobb也很重要。
这对解决了“连续”和“平滑”闭合曲线的问题。连续性意味着不间断。光滑度意味着连续性,没有角落。如果用纸和铅笔坐在办公桌前,您可能会绘制出平滑连续的曲线。格林说,他们“更易于合作”。
平滑连续曲线不同于简单的连续曲线,但不同于平滑曲线,例如与方形桩的Toeplitz猜想有关的曲线。这样的曲线可以具有拐角-曲线突然偏离并沿不同方向行进的点。多角度曲线的一个主要示例是类似雪花的分形科赫曲线。,实际上包含一些角落。科赫雪花和其他类似曲线无法使用代数方法进行分析,这使得它们特别难以研究。
丹恩说:“有些连续的(不平滑的)曲线令人作呕。”
尽管如此,由Green和Lobb解决的问题仍属于平滑曲线,因此属于连续曲线。他们没有研究出在这样的曲线上是否总是有四个点形成一个正方形-对于平滑的连续曲线,这个问题在1929年得到解决-他们研究了另外一些东西:在这些曲线上总是有四个点形成任何给定的矩形比例,即任何纵横比。对于正方形,此比例为1:1;对于高清电视,此比例为16:9。

矩形钉问题的第一个重大突破是赫伯特·沃恩(Herbert Vaughn)在1970年代后期发现的证据。它提供了一种查看矩形几何形状的新方法,并提供了后来被其他数学家(包括Green和Lobb)使用的几种方法。
格林说:“每个人都知道这一证明。” “这几乎是民间的,您可以通过在餐桌上讨论一切来了解这些东西。”
沃恩没有将矩形想象成四个相连的点,而是将其想象成相互关联的两对点。

想象一个具有顶点ABCD的矩形。其中,点AC之间(对角线上)的距离等于点BD之间(另一对角线上)的距离。而且,这些对角线恰好在中间相交。
因此,在闭环上搜索矩形时,可以搜索位于相交的相同线段末端的成对点。要找到它们,重要的是要有系统地描述它们。
要了解这意味着什么,让我们从简单一些开始。拿数字线。让我们在上面选择两个点-假设数字7和8-并将它们构造为数字平面(7,8)上的一个点。我们还可以建立点,它们是一对相同的数字(7、7)。现在,让我们考虑在数字行上可以找到的所有可能的数字对(其中有很多!)。如果我们建立所有这样的数字对,那么我们将填满整个数字平面。表示这种情况的另一种方式是说数字平面“参数化”,即它以有序的方式收集数字线上的所有数字对。
沃恩对闭合曲线上的成对点做了类似的处理。就像数字线一样,它只是一维封闭。他意识到,如果您用一条曲线成对的点,然后从中建立一个图形(并且哪个坐标是x坐标,哪个坐标是y都没有关系),那么该平面将无法工作。取而代之的是,您得到一个意外的图形-Mobius条带,即只有一侧的二维曲面。

从某种意义上讲,这是很合逻辑的。要了解原因-在曲线上选择一对点,并分别命名为x和y。现在从x移至y,沿曲线的一部分移动,同时-从y移至x,沿曲线的相反方向移动。在此过程中,您将遍历曲线上的所有点对,并以无序对(x,y)开始和结束。但是,这将使您回到最开始-只有最后的点序列才与初始点相反。莫比乌斯地带的本质是一圈乱序的点,其方向相反。
该功能区为数学家提供了一个新对象,可以将其作为矩形挂钩问题的一部分进行分析。沃恩利用这一事实证明,在任何曲线上,至少有一组四个点组成一个正方形。
四维答案
Green和Lobb的证明基于Vaughn的工作。但是,它也结合了其他一些发现,其中一些是相对较新的。最终证明就像是一种精确的工具,其最终结果取决于经过认真考虑的思想组合。
证明的第一批主要证据之一是2019年11月,当时普林斯顿大学博士生科尔·休格迈尔(Cole Hugelmeyer)发表了论文展示了一种分析沃恩使用的莫比乌斯带的新方法。它使用了称为嵌套的数学过程,即当我们将一个对象投影到几何空间上时。结果,格林和洛伯采用了休格尔迈尔的技术,并将其转移到另一个几何空间。但是要了解他们的所作所为,您首先需要了解他的所作所为。
这是一个简单的嵌套示例。
让我们从一维线开始。直线的每个点由一个数字定义。现在,我们将这条线嵌入二维空间中-也就是说,将其绘制在平面上。
在xy平面上嵌入一条直线后,其中的每个点已经由两个数字确定-x和y坐标,它们描述了该点在平面上的确切位置。现在,您可以使用2D几何技术分析线。
Hugelmeyer的想法是采用类似Mobius条的方式,但将其嵌入4空间中,其中4维几何的属性将允许您证明所需的结果。
“基本上,您有一个Mobius条,并且需要为每个点分配四个坐标。 Lobb说,这就像是在二维空间中的点的地址。
Hugelmeyer分配这些地址的方式很容易达到主要目标,即在曲线上找到矩形。可以说,他为曲线上的每个点分配了类似邮政地址的信息-州,城市,街道名称和门牌号码。
为此,他从Mobius条上的特定点开始,并在她表示的原始闭合曲线上获得了这两个点。然后,他找到了连接这些点的线段的中点,并确定了它的x和y坐标。我们得到了三维地址的前两个值(州和城市)。
然后,他测量了曲线上两个原始点之间的距离。该长度成为三维地址(街道名称)的第三个值。最后,他计算了连接两个原始点的线段与x轴之间的角度。该角度成为三维地址(门牌号)的第四个值。这四个值告诉您关于曲线上的一对点的所有信息。

这项练习听起来很有挑战性,但很快就收到了回报。休格迈尔接过所附的莫比乌斯地带,将其转过来。旋转的莫比乌斯带已相对于其原始位置移动,并且带的两个副本相交。由于转弯是在四维空间中进行的,因此很难想象莫比乌斯带的自相交形状-但很容易用数学来描述。
这个交叉路口非常重要。当Mobius条带的两个副本彼此叠加时,可以在原始闭合曲线上找到两对点,从而形成矩形的四个顶点。
为什么?
首先,请记住,矩形可以表示为两对点,两对点的相同交点的公共相交中心将它们连接起来。正是此信息被编码在分配给嵌套莫比乌斯带的每个点的三维地址的前三个值中。
其次,在四维空间中,您可以展开Mobius条带,从而仅更改其四维地址中每个点的一个坐标-门牌号会更改,但街道,城市和州仍然保留。例如,请记住,如果拿一块砖,将其放在自己的前面,然后向右移动,那么只会改变其x坐标,而不会改变y或z。
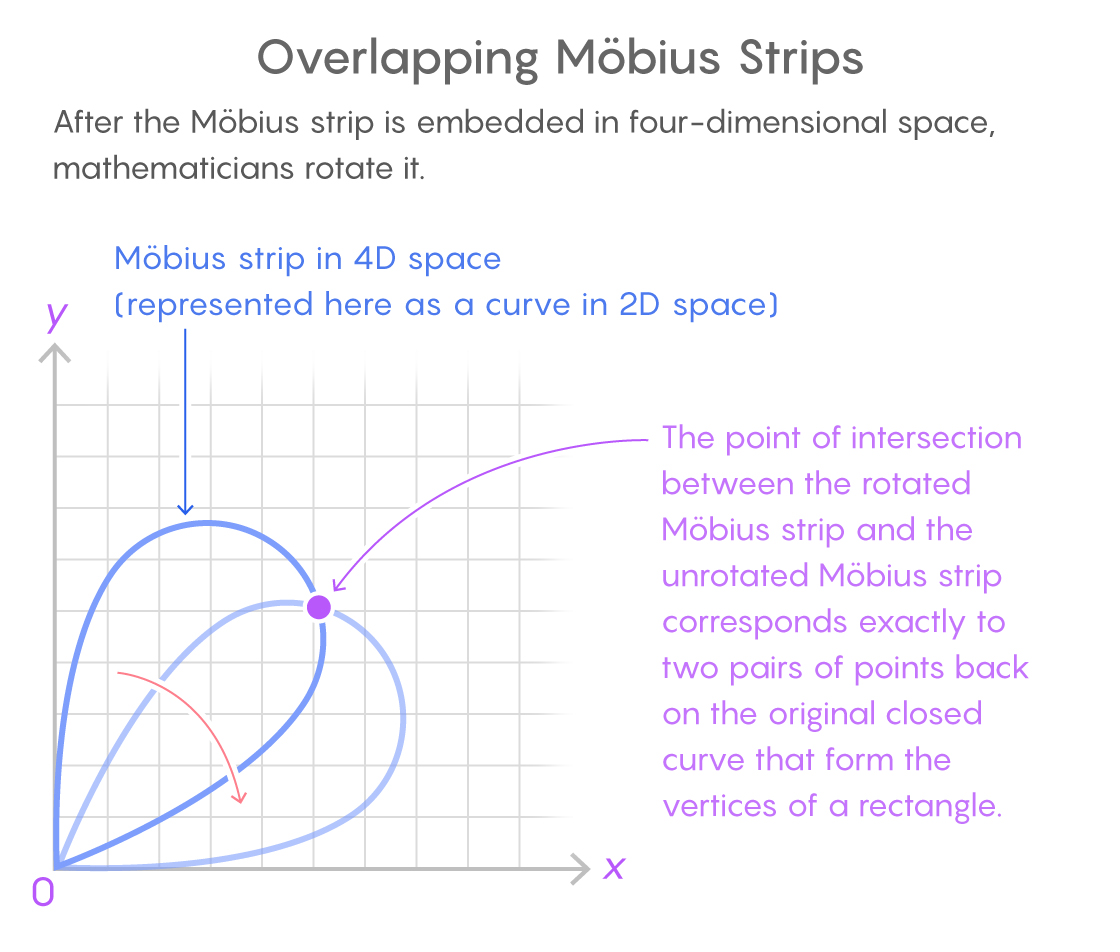
此处的二维空间中的莫比乌斯带由二维曲线表示。两个副本的交点对应于原始闭合曲线上形成矩形的两对点。
Hugelmeyer解释了如何在四维空间中旋转Mobius带,以使指示连接线对的线的中点的两个坐标不变-指示点对之间的距离的坐标也不变。它的旋转仅更改了最后一个坐标-包含有关连接点的线段所处角度的信息。
结果,莫比乌斯带的旋转副本与其原始副本的交点恰好对应于位于闭合曲线上的两对点,它们具有共同的中心(连接它们的线段的交点)并且彼此之间的距离相同。即,该交点对应于曲线上矩形的四个顶点。
长期以来,使用两个空间的交点找到正确点的策略一直用于解决方形和矩形钉的问题。
丹恩说:“在这些空间的交点处是理想的空间。” “方钉钉子历史上的许多证据都具有这种想法。”
休格迈尔在四维环境中使用了交叉路口策略,比他能获得的任何东西都多。 Mobius条带可以从0°到360°任意角度旋转,他证明了所有这些旋转的三分之一导致了原件与旋转后的副本相交。这等效于声明您可以在闭合曲线上找到具有所有可能长宽比的三分之一的矩形。
格林说:“让Cole考虑将Mobius条带放入4D空间并使用4D技术值得称赞。”
同时,休格迈尔的结果被证明是具有启发性的:如果四维空间对于解决这个问题是如此有用,为什么对所有矩形中只有三分之一有用呢?
格林说:“毕竟,必须有一种方法来获得剩余的三分之二。” -但是呢?”
辛方法
格林和洛伯对大钉子的问题很感兴趣,甚至在大流行病把它们送回家之前也是如此。 2月,Lobb在冲绳科学技术学院主持了一次会议,格林也参加了会议。这对夫妇花了几天时间讨论这项任务。此后,他们又在观看东京风光的过程中又进行了一周的讨论。
“我们还没有停止讨论这个问题,”洛布说。 “我们去了餐馆,咖啡馆,博物馆,不时对此有所考虑。”
即使被锁在家中,他们仍继续讨论。他们希望证明Mobius条带的任何旋转都会给出一个交点-等同于找到任何比例的矩形。
4月中旬,他们制定了战略。这意味着将磁带嵌入特殊的三维空间中。常规嵌套意味着您可以以任何方式放置所需的对象。想象一下,可以在二维平面中嵌入一维闭合曲线的方法有多少种,它们的数量是无限的,因为您可以通过无数种方法将线程绑在表上。
但是,让我们说,您在其中嵌套循环的二维表面具有其自己的结构。例如,想象一下一个带有箭头(或矢量)的地图,向我们指示风向地球表面的吹动方向和速度。现在,您在每个点都有2D曲面,其中包含其他信息或结构。
然后,您可以引入限制-必须在地图上放置一维RFP,以使其始终遵循地图上箭头的方向。
Schwartz说:“您正在限制事物,以使曲线遵循这些向量。”现在,您可以使用更少的方式放置曲线。

其他几何空间可能会施加不同的约束。所谓格林和洛伯的工作很重要。辛空间。
这个几何概念最早出现在19世纪,当时研究的是诸如绕行星运行的物理系统。行星在三维空间中移动的位置由三个坐标确定。但是,正如爱尔兰数学家威廉·罗恩·汉密尔顿(William Rowan Hamilton)所说,也可以在行星运动路径的每个点上放置一个表示动量的矢量。
在1980年代,苏联和俄罗斯数学家弗拉基米尔·伊戈列维奇·阿诺德(Vladimir Igorevich Arnold) 开展了辛几何的研究。他意识到,辛结构的几何空间在旋转时,与不具有这种结构的空间相比,相交的频率更高。
这对于Green和Lobb来说是完美的选择,因为他们想解决所有比例的矩形钉问题,从而证明旋转的参数化Mobius条形副本也经常相交。因此他们开始尝试在二维辛空间中嵌入二维莫比乌斯带。格林说:“一个全新的想法是从辛几何的角度解决这个问题。” “那改变了一切。”
到4月底,格林和罗布确定可以在四维辛空间中嵌入莫比乌斯带,使其与结构一致。之后,他们可以开始使用辛几何工具,其中许多与自相交问题直接相关。
洛布说:“如果可以使莫比乌斯带服从辛规则,则可以使用某些辛定理。”
Green和Lobb确信可以改善Hugelmeyer的结果-也就是说,证明相交不仅发生在所有拐角的三分之一处。这意味着从曲线的各个点将有可能制作出具有所有可能比例的三分之一以上的矩形。
Lobb说:“当我们有了这个想法时,很明显将会发生一些事情。”
但是,结果却更加笼统,并且出现的速度比预期的要快得多。多亏了一个奇怪的数学对象- 克莱因瓶(Klein bottle),它在辛几何的背景下具有一个重要的特性。
克莱因瓶连接
Klein瓶子是一个二维表面,看起来像一个现代派的水罐。与Mobius条带一样,它只有一个表面,可以通过粘合两个Mobius条带来制作。您可以收集并放置在桌子上的所有Klein瓶子(就像许多数学家一样)都是相互交叉的。不可能将Klein瓶子放在三维空间中,以使其不会交叉。
Schwartz说:“ Klein瓶子必须是一个表面,但其手柄需要突破瓶子才能从外到内。”
但是,不一定是这种情况。 Klein瓶子可以嵌套在4D空间中,以使其不相交。第四维为回旋提供了空间,而克莱因瓶可以绕开自身。这可以与两个人在一维的直线上相互走来避免碰撞的方式进行比较,但是如果他们在二维的地板上走动,他们很容易转身离开。

今年五月,绿色和洛布回忆一个事实有关克莱因瓶-它不能被嵌入在一个四维辛空间,使其不相交本身[从工作另一位俄罗斯数学家,梅耶·维克托Shevchishin关于Klein瓶在四维空间中的拉格朗日嵌入法。翻译]。换句话说,没有自交的克莱因瓶就不能满足辛空间的所有要求。这一事实成为证明的关键。格林说:“那是一根魔杖。”
这就是为什么。 Green和Lobb已经表明,可以在四维辛空间中嵌入Mobius带,从而满足他的要求。他们只需要弄清楚莫比乌斯带的每一匝是否与原始副本相交。
但是,两条相交的Mobius条带相当于一个Klein瓶,它在这样的空间中相交。而且,如果旋转Mobius带,使旋转后的副本不与原件相交,则会得到一个不会交叉的Klein瓶子。但是这样的克莱因瓶不可能存在于四维辛空间中。因此,嵌套莫比乌斯带的任何可能旋转也必须相交-即,在每个闭合的平滑曲线上,可以找到四个点,它们形成了任意比例的矩形。
证明的结尾像雪崩一样击中读者。
Denn说:“首先要进行设置,设置,设置,然后发出咕unt声,并且证明已经准备就绪。”
Green和Lobb的证明是解决问题通常依赖于找到正确观点的一个很好的例子。几代数学家无法解决此版本的矩形钉问题,因为他们试图在更传统的几何条件下解决该问题。当格林和洛伯将问题带到辛辛那苦世界时,它很容易解决。
格林说:“这些问题在1910年代和1920年代出现,没有合适的平台来反思它们。” “现在我们开始了解到它们实际上是辛辛苦现象的隐藏化身。”