碰撞检测与分割轴定理

如今，计算机是功能强大的计算机，

能够每秒执行数百万次操作。当然，您不能不模拟现实世界或游戏世界。计算机建模和仿真的问题之一是确定两个物体的碰撞，其解决方案之一是通过分离轴上的定理来实现的。







注意。本文将举一个带有2个平行六面体（以下简称为立方体）的示例，但其他凸对象的想法将保留下来。

注意。所有实现将在Unity中完成。

行动0。一般理论

首先，您需要熟悉“ 分离超平面定理 ”，它将成为算法的基础。



定理。当且仅当两个凸几何之间存在一个将它们分开的超平面时，两个凸几何才不相交。正交于分割

超平面的轴称为分割轴，并且图形在其上的投影不相交。





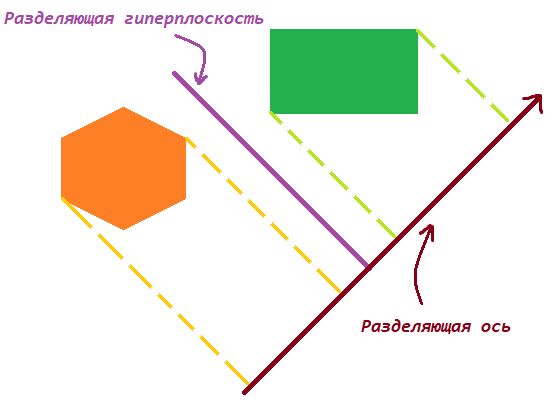
分割轴（2D情况）





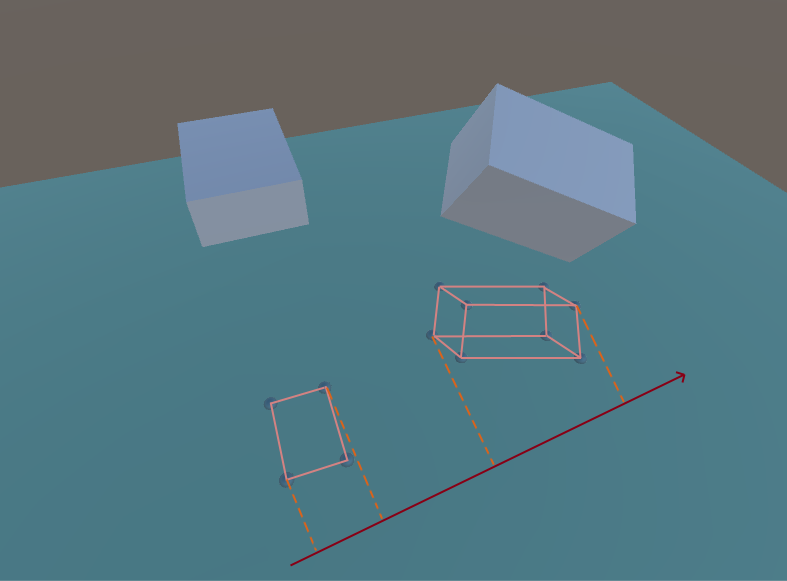
分割轴（3D情况）

您可能会注意到，分割轴上的投影没有相交。



属性。势能划分轴将分为以下几组：

• 每个立方体的平面规范（红色）
• 立方体边缘的矢量积 $$，$\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$

   其中X是第一个立方体的边缘（绿色），Y是第二个立方体的边缘（蓝色）。







我们可以使用以下输入数据描述每个多维数据集：

• 立方体中心坐标
• 立方体尺寸（高度，宽度，深度）
• 立方体四元数

让我们为此创建一个附加类，该类的实例将提供有关多维数据集的信息。

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

行为1.四元数

通常，物体可以在空间中旋转。为了找到顶点的坐标，并考虑到立方体的旋转，您需要了解什么是四元数。



四元数是一个高复数，它确定对象在空间中的旋转。

$$

$$w+xi+yj+zk$$

虚数部分（x，y，z）代表定义旋转方向的矢量，

实数部分（w）定义进行旋转的角度。



它与所有通常的欧拉角的主要区别在于，与在三个子空间中旋转对象的三个线性独立向量相比，拥有一个可以确定旋转方向的向量就足够了。 我建议的两篇文章 去到约四元数更多详细信息：一两个现在，我们有四元数的最小的理解，让我们了解如何旋转向量和描述了一个四元数旋转的矢量的功能。 矢量旋转公式

$$

$$\vec{v}' = q * \vec{v} * \overline{q}$$

$$是必需的向量$\vec{v}'$

$$是原始向量$\vec{v}$

$$四元数$q$

$$ -四元数逆 首先，让我们给逆四元数的概念中的标准正交基-它与虚数部分的符号相反四元数。$\overline{q}$







$$$q = w+xi+yj+zk$

$$ 计算$\overline{q} = w-xi-yj-zk$



$$$\vec{v} * \overline{q}$



$$$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

$$$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

$$$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

$$$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$



现在我们写出该产品的各个组件并收集新的四元数

$$$M = u_w+u_xi+u_yj+u_zk$

$$$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

$$$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

$$$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

$$$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$



让我们数一下其余部分，即 $$$q*M$并获得所需的向量。



注意。为了避免计算量过大，我们仅介绍此乘积的虚部（向量）。毕竟，她是表征所需矢量的特征。



$$$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

$$$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

$$$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

$$$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

$$$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$



让我们收集向量的成分



$$$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

$$$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

$$$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$



$$$v' = (v_x', v_y', v_z')$

这样就获得了所需的向量，



编写代码：

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

第二步：找到一个立方体的顶点

知道如何使用四元数旋转向量，将不难找到立方体的所有顶点。



让我们继续进行查找立方体顶点的功能。让我们定义基本变量。

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

接下来，您需要找到一个点（锚点），从该点最容易找到其他顶点。



从中心坐标上减去立方体尺寸的一半，然后将一个立方体尺寸添加到枢轴点。

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

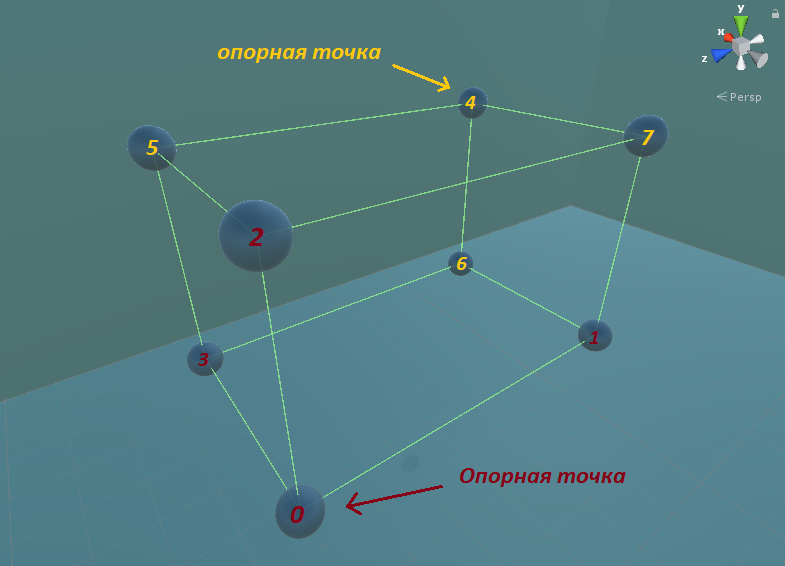
我们可以看到这些点是如何形成的



。找到顶点的坐标后，有必要将每个矢量旋转相应的四元数。

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

让我们继续进行预测。

行动3.搜索分割轴

下一步是找到声称要分割的轴集。

回想一下，可以在以下几组中找到它：

• 每个立方体的平面法线（红色）
• 立方体边缘的矢量积 $$$\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$其中X是第一个立方体的边缘（绿色），Y是第二个立方体的边缘（蓝色）。

为了获得必要的轴，具有四个立方体的顶点就足够了，它们形成矢量的正交系统。这些顶点位于第二步中形成的点阵列的前四个单元中。







有必要找到矢量生成的平面法线：

• $$$\vec{a}$ 和 $$$\vec{b}$
• $$$\vec{b}$ 和 $$$\vec{c}$
• $$$\vec{a}$ 和 $$$\vec{c}$

为此，有必要在立方体的各对边缘上进行迭代，以使每个新样本形成一个与所有先前获得的平面正交的平面。我很难解释它的工作原理，因此我提供了两个版本的代码来帮助您理解。





但是您可以使它更容易：

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

我们还必须找到立方体边缘的所有向量积。这可以通过简单的搜索来组织：

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

动作4.轴上的投影

我们到了最重要的时刻。在这里，我们必须找到立方体在所有可能的分割轴上的投影。该定理有一个重要的结论：如果物体相交，则立方体投影的相交最小的轴为碰撞的方向（法线），相交段的长度为穿透深度。



但首先，回想一下向量v在单位向量a上的标量投影的公式：

$$

$$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

现在我们将描述一个确定候选轴上投影交点的函数。



输入是两个多维数据集的顶点，以及一个可能的分割轴列表：

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

在轴上的投影由在轴本身上具有最大值和最小值的两个点设置：







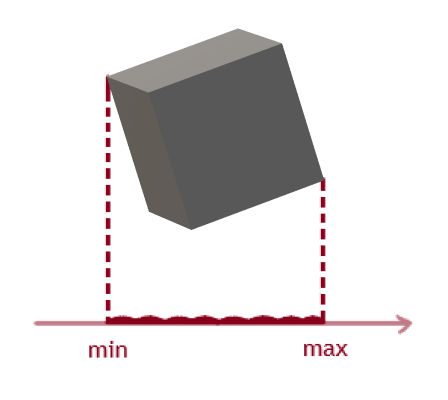
接下来，我们创建一个函数来返回每个立方体的投影点。它带有两个返回参数，一个顶点数组和一个可能的分度轴。

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

因此，应用此函数（ProjAxis），我们可以获得每个立方体的投影点。

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

接下来，基于投影顶点，我们确定投影的交点：







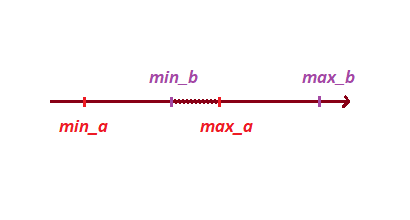
为此，让我们将点放入数组中并对其进行排序，此方法不仅将帮助我们确定交点，而且还将确定交点的深度。

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

请注意以下属性：



1）如果线段不相交，则线段的总和将小于所形成的极点的线段：







2）如果线段相交，则线段的总和将大于所形成的极点的线段：







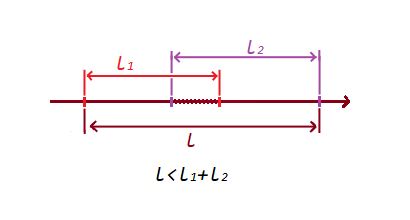
在这种简单条件下，我们检查了相交和非相交段。



如果没有相交，则相交深度将为零：

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

因此，对于我们来说，至少有一个矢量，立方体的投影不相交，然后立方体本身不相交就足够了。因此，当我们找到分割轴时，我们可以跳过检查剩余的向量并终止算法。



在立方体相交的情况下，所有事情都更加有趣：立方体在所有矢量上的投影都将相交，并且我们必须定义具有最小交集的矢量。



让我们在循环之前创建此向量，然后将长度最小的向量存储在其中。因此，在循环的最后，我们得到了所需的向量。

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

每次找到投影相交的轴时，我们都会检查其长度是否最小。我们将这样的轴乘以相交的长度，结果将是所需的立方体相交的法线（方向）。



我还添加了相对于第一个立方体的法线方向的定义。

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

结论

带有实施和示例的项目已上载到GitHub，您可以在此处查看。



我的目标是分享我在解决与确定两个凸对象的相交有关的问题方面的经验。讲述这个定理也是容易理解的。