
非常感谢。我为坐在这里表示歉意。我是一个很老的男人。
今天的主题在某种意义上非常特别,因为它很古老。纽结是人类生活中不可或缺的一部分,它们始终存在。古人对此进行了写道。这件事在很大程度上是我们无法控制的。从某种意义上说,它们似乎是一种极端的并发症-完全是一团糟。
有许多类型的障碍。因此,纯属巧合,很多年前,我开始处理这种形式的并发症,令我感到完全惊讶的是,我发现了迹象,而且我必须说,有很明显的秩序混乱迹象。因此,今天我想向您介绍一些这意味着什么的例子。我更喜欢“残破”而不是“不均匀”,因为对于像我遥远的年轻人一样学习拉丁语的人来说,不平衡是均匀的对立面。但这种情况并非如此。
平等是破裂的对立面,因为在我们看来,大部分世界都充满了破裂。
让我向您展示几个对象。其中一些是人为创建的。在某种意义上,其他人是非常真实的。这才是真实的。

这是花椰菜。为什么我要向您展示花椰菜,一种普通的古老植物?因为尽管它是例行和古代的,但它却是复杂而简单的。它既复杂又简单。例如,称量它并不难。如果我们要吃的话,体重很重要。但是假设我们要测量它的表面。这变得越来越有趣。用锋利的刀切出一朵花椰菜花,仔细观察,我们看到整个花椰菜,只有较小的大小。然后,您可以一次又一次地切,一次又一次地切。。。您会得到越来越小的花椰菜标本。人类的经验表明,有些形式具有如此有趣的特性,即每个部分都与整体相似,但尺寸较小。这个人从这个事实中学到了什么?很少
在研究这个问题的过程中,我发现了一些完全令人惊奇的东西:扭结可以用一个数字来衡量,例如2.3或1.2,有时甚至更多。有一天,我的一个朋友带来了一张照片,开玩笑地问:“这条曲线的纽结是什么?”我说:“略少于一半。”事实证明,它等于1.48。我花了很长时间研究这些东西才花了很长时间。所讨论的数字表示表面的断裂程度。

让我马上保留一下,这些表面绝对是人造的,并且是在计算机上创建的。唯一的起点是数字。这个数字很奇怪。左侧的断裂是从多个景观复制的结果。在右边-我自己设定了更高的扭结。如果仔细观察,一段时间后您可以用肉眼识别这两种情况的差异。
人必须适应骨折的概念。这是很坏的,但是,也许有人会说,这很平滑,但是这是完全平滑的。很少有事情能顺利进行。现在让我们问自己一个问题:花椰菜的表面是什么?它可以被测量以及被测量...被测量的越精确,表面越大,等等,直到很小的距离。这些湖泊的海岸线长度是多少?测量越精确,结果越长。海岸线长度的概念由于经常被引用而显得如此明显,实际上是完全错误的:根本没有这样的东西。必须有不同的方法。
知识的用途是什么?令人惊讶的是,有很多好处。首先,我想说的是,我不断发明的人造景观被用于摄影。我们看到远处的群山。它可能是山脉,但很可能只是流动的公式。这很容易实现。过去花了很长时间,但现在只是小事了。在这里看看。这是真实的光芒。
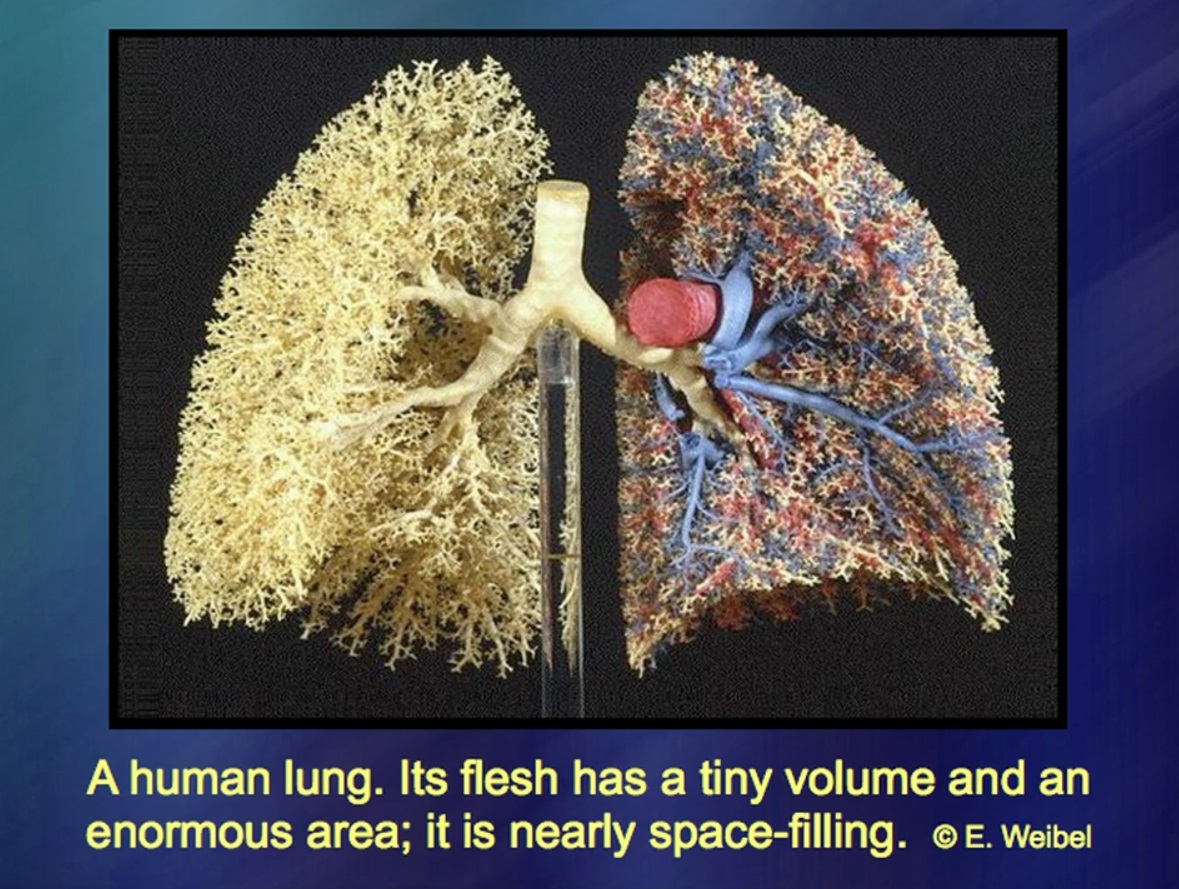
肺是一个非常奇怪的物体。众所周知,它有一定的分量。还已知肺的体积很小。那肺面积呢?解剖学家长期以来一直在争论这个问题。据信在一个正常的男人中,肺的面积等于一个篮球的面积。其他人则认为,没有五个这样的球。差异是巨大的。为什么?因为肺区域是一个非常模糊的定义概念。支气管的分支和分支越来越深。而且它们停止分支的原因不是因为某些原理,而是由于纯粹的生理条件,是由于肺内的粘液。这就是如何形成更大的肺:支气管越来越深地分支,而它们之间的间隙对于鲸鱼,人和小啮齿动物来说几乎是相同的。
那么,这有什么用呢?令人惊讶的是,直到最近,解剖学家对肺部结构的认识仍然很差。我认为,我的数学研究令人惊讶的是,它对研究肺部疾病以及肝脏疾病的外科医生很有帮助,因为那里的分支系统缺乏可理解的几何形状。换句话说,我必须为没有自己的几何图形的对象创建几何图形。发现了令人惊讶的品质:通常,这种几何形状的规则非常简洁。您从简短的公式开始,多次应用它们,有时重复应用。同样的重复。最终结果是这样的。
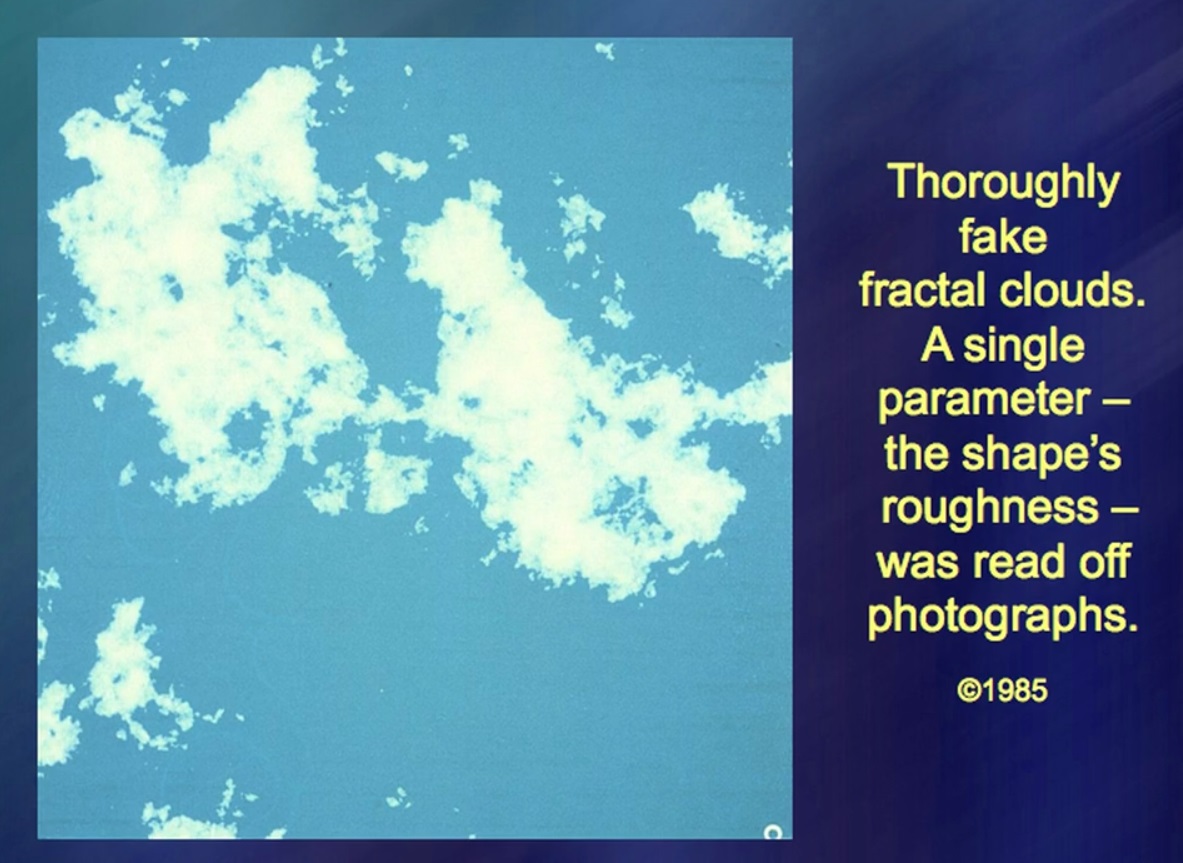
这种云是完全人造的,100%。好吧,99.9%。这里唯一的自然元素是数字,即云的破裂-这个数字来自自然。像云这样复杂的事物,如此不稳定,易变,遵循一个简单的规则。这个简单的规则不能解释云量。但是云海必须考虑到这一规则。我不知道这些旧照片有多完美。我做了很深入的工作,但随后我的注意力转向了其他现象。
这是另外一件有趣的事情。数学史上的革命性事件之一是大约130年前,145年前发生的,但许多人对此没有足够的重视。数学家开始创造不存在的形式。在数学家中,人们创造出一种自然界中不存在的东西的能力已经得到人们的赞赏,而且这种程度是绝对无法想象的。特别是,他们能够发明一条曲线,将整个平面填充到最后一个点。曲线是曲线,平面是平面,并且两者不匹配。事实证明它们确实适合在一起。
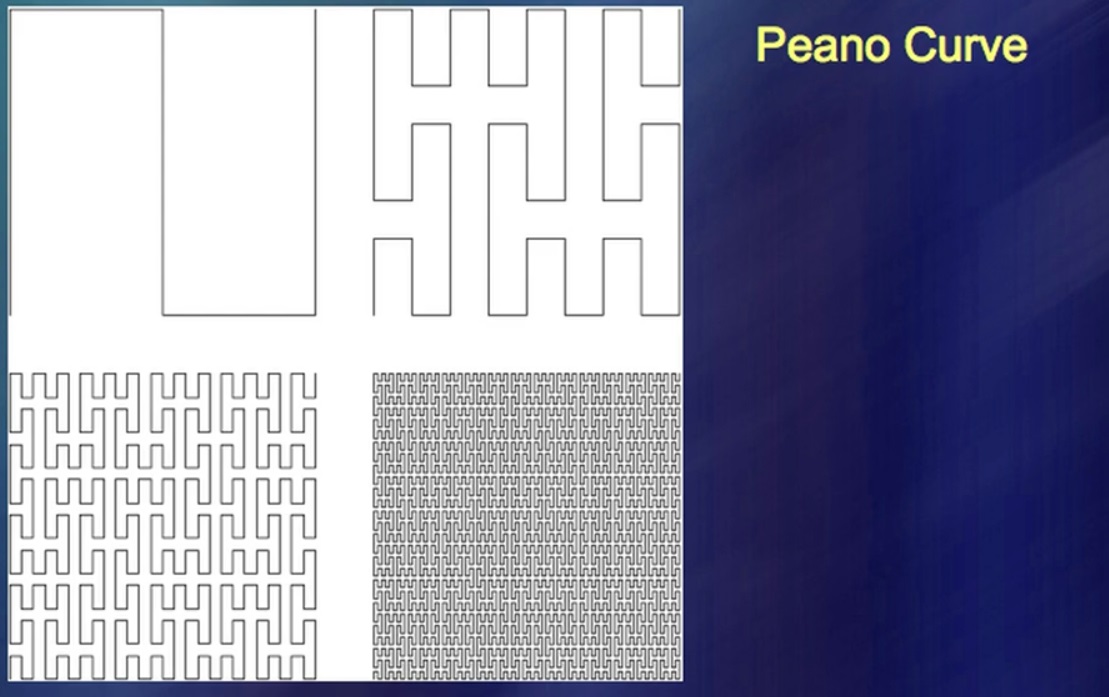
一个名叫皮亚诺(Peano)的人发现了这种曲线,并引起了极大的兴趣。它们非常重要,并且引起了人们的极大兴趣,因为在某种程度上,数学已经分为基于现实的数学划分和基于纯粹理性的数学划分。不幸的是,我偶然证明,由于纯粹的原因而被人们了解的事实,实际上早已以另一种形式被人们所熟知。在这里,我有一个以曲线形式填充平面的小溪系统。

就其本身而言,这就是历史。那是在1875年和1925年之间,这是数学正准备脱离现实世界的绝佳时机。从我的童年和我的学生时代开始,某些对象就说明了这种差距,数学和可见现实之间的差距。但是,我设法重新思考它们,将它们颠倒过来,并在它们的帮助下描述了自然复杂性的某些方面。
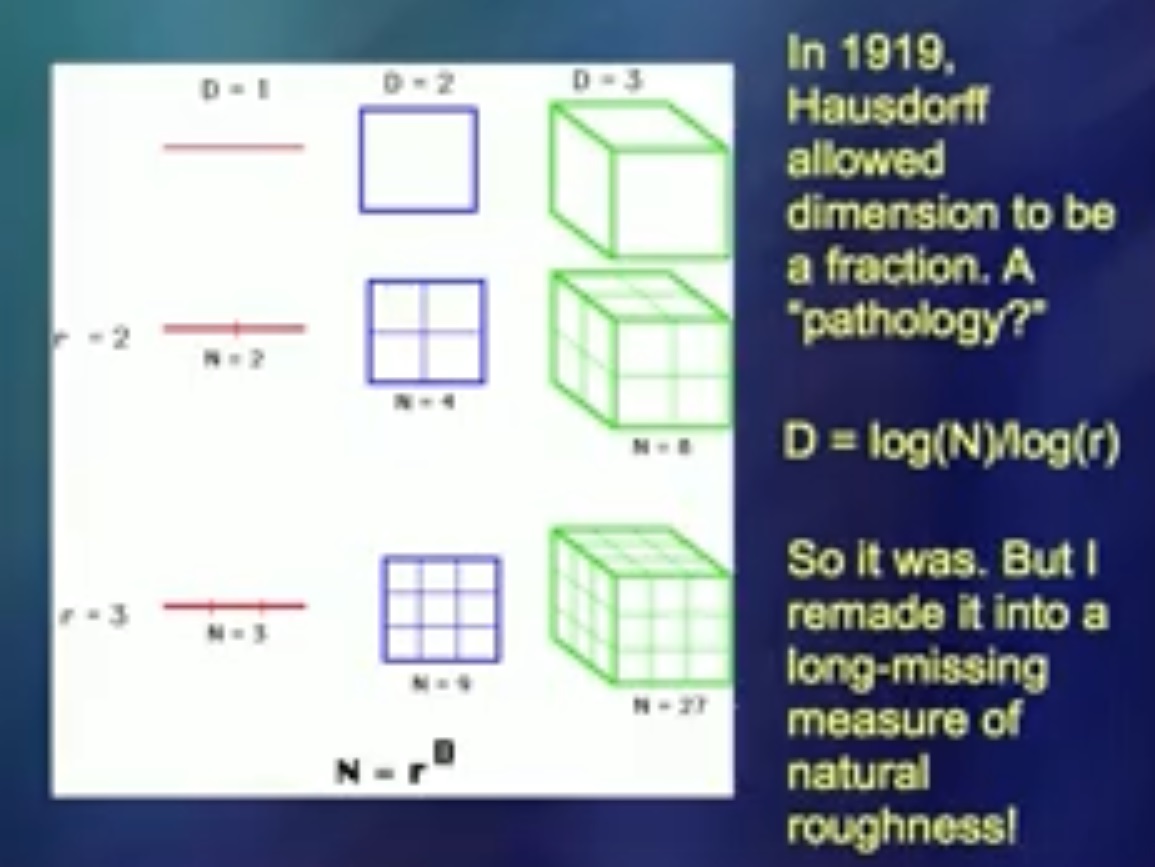
1919年,一个名叫Hausdorff的人发现了一个数字,可以算是一个数学笑话。但是我发现这个数字是衡量扭结的好工具。当我第一次告诉我的同事时,他们说:“别傻了。这是……”实际上,我没有做愚蠢的事情。

伟大的画家北斋对此非常了解。图片的底部是藻类。北斋不知道必要的数学:那时它根本不存在。此外,他是日本人,(当时)与西方没有任何接触。但是艺术早已包含分形元素。我可以谈论很长一段时间。

艾菲尔铁塔具有分形元素。我读了埃菲尔铁塔的书,关于他的铁塔-他的理解范围令人惊讶。
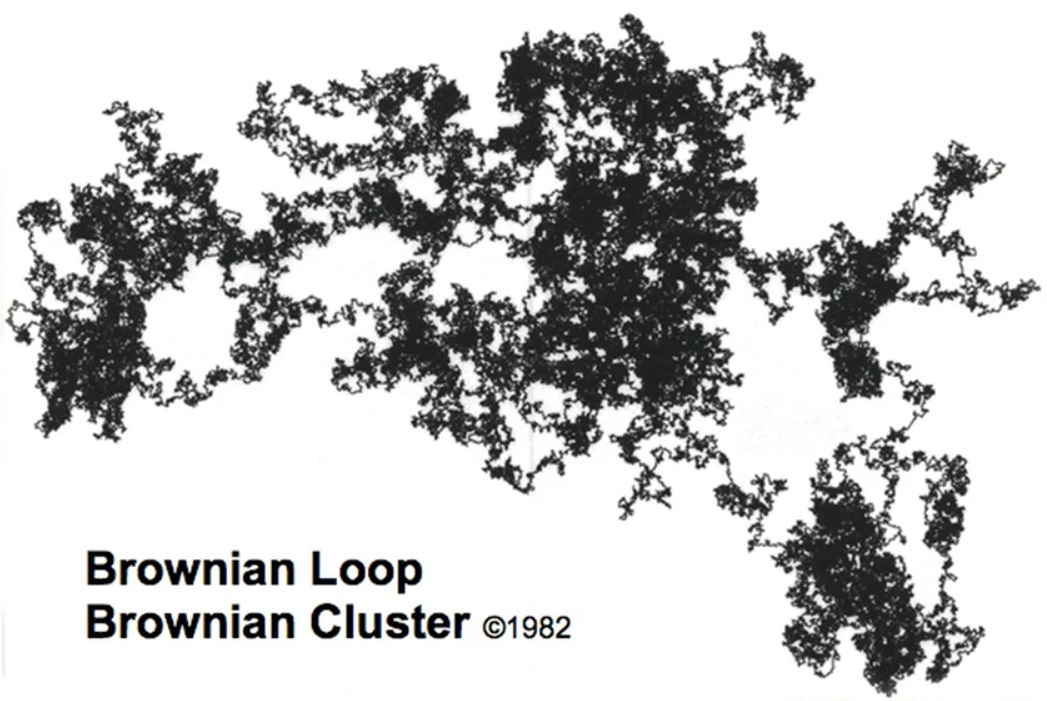
这是一团糟。布朗环。一旦我确定自己已经度过了职业生涯的相当一部分,那么多不同的事情困扰着我,于是我决定该测试一下自己了。我是否可以探索每个人都已经探索了很长时间的物体并在其中找到全新的东西?我开始研究布朗运动范畴内的所有东西。我尝试了不同的角度,尝试了不同的方法,然后回到了起点。然后我向助手建议:“我在这里什么都看不到。你可以涂满吗?”他这样做了,也就是说,他充满了所有内心。 “我管理…”

但我大喊:“停!停止!停止!理解:这是一个小岛。”惊人。布朗运动的扭结等于二。我测量一下,结果是1.33。我一次又一次地测量。长时测量,布朗运动大。再次:1.33。数学问题立即出现:如何证明它?我的朋友花了20年。三人的证据不完整。他们共同努力,并设法获得证明。结果,他们被授予数学家著名的[菲尔兹]奖章。总体而言,数学家因证明了我看到但无法证明的事实而获得了三枚[Fields]奖章。
现在人们到处问我:“一切是如何开始的?您的学习是如何导致您遇到这种不寻常的事情的?”
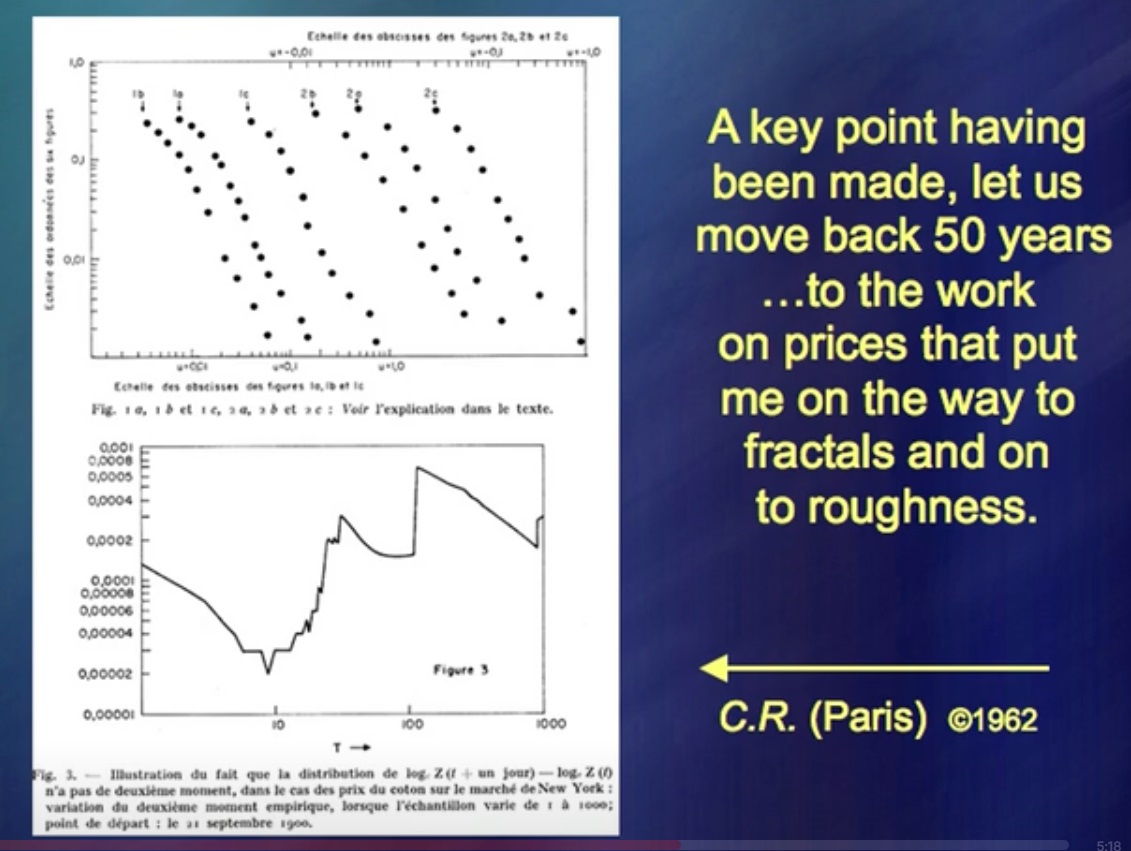
是什么让我可以同时成为机械工程师,地理学家,数学家等?奇怪的是,但我首先研究了股票市场的价格。

我有一个理论,并写了有关它的书。
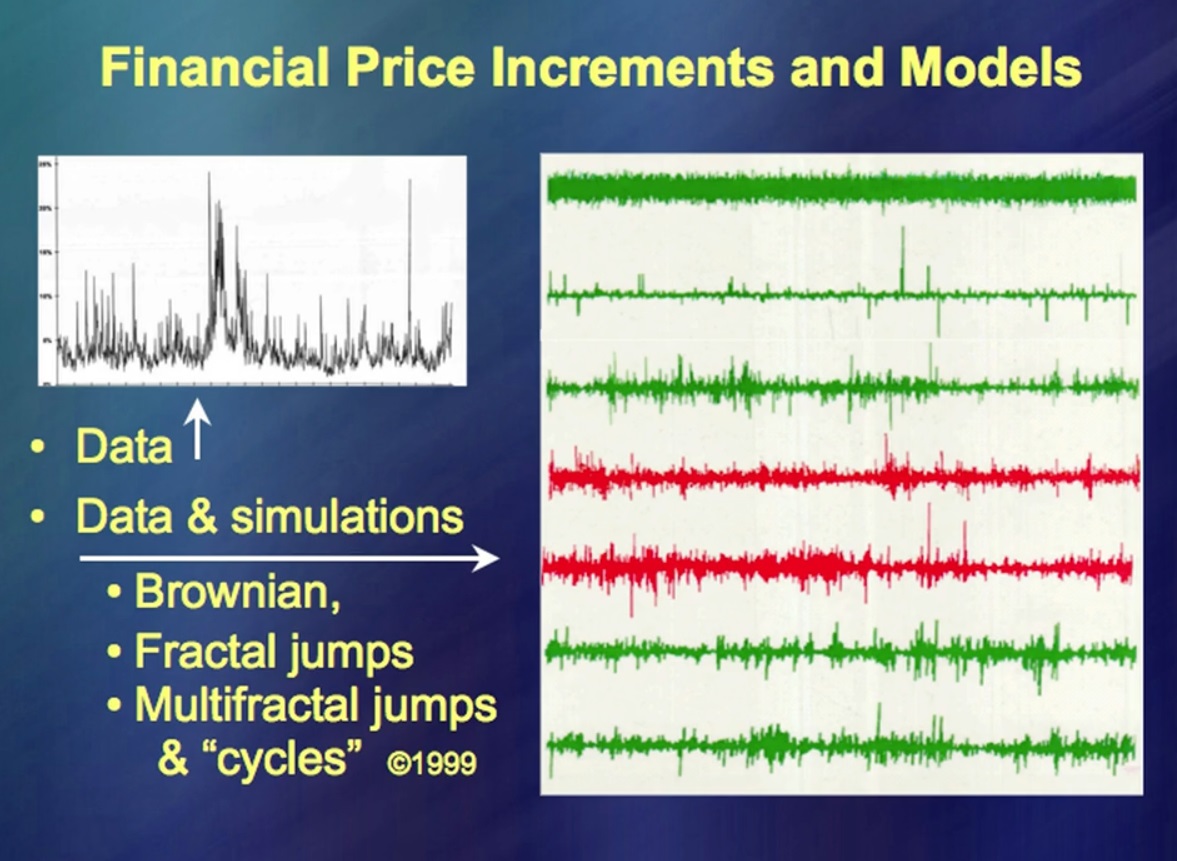
“金融工具的价格变动”在左边,您可以看到很长时间的数据,在右边,则是顶部-根据非常非常流行的理论得出的数据。它非常简单,您可以很快写很多关于它的书。 (众笑)关于这一主题的书籍有数千本。现在与实际价格走势进行比较。他们在哪里?其他行包括实际价格变动以及我的小额假货。那里的主要思想是您需要能够做...这叫什么? …模拟价格波动。这在50年前非常有效。
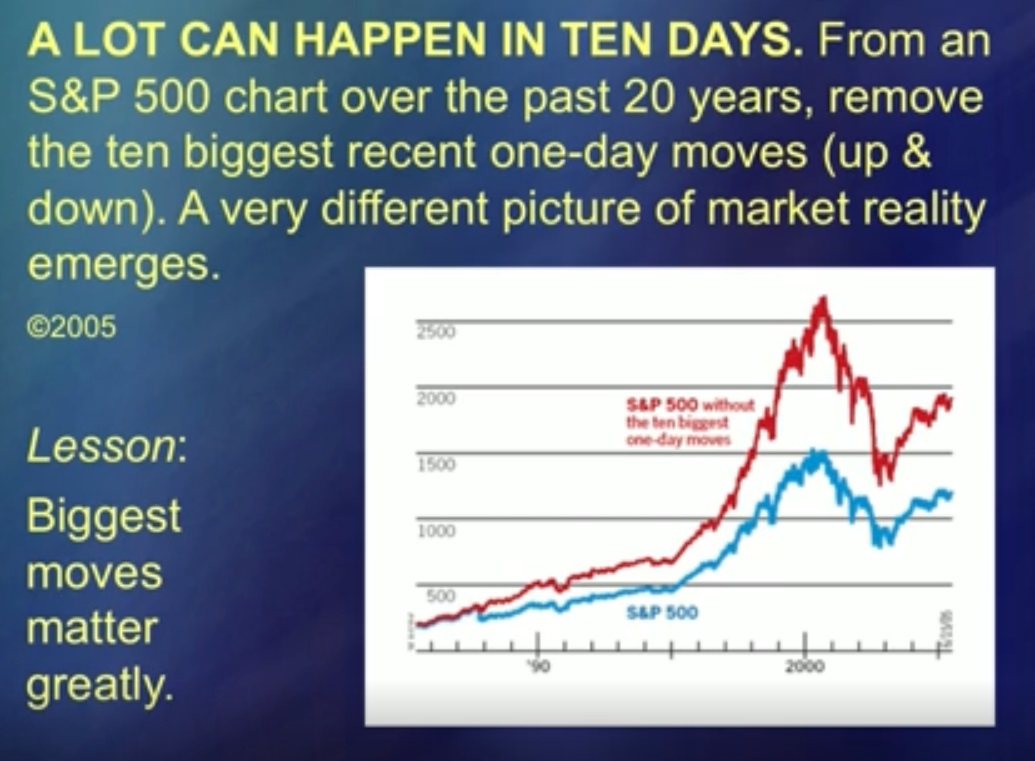
50年来,我的想法一直很荒唐,因为它可以更轻松地完成。但是现在,我告诉你,他们开始听我说。 (笑声)这两条曲线代表平均值。蓝色是标准普尔(S&P 500),红色是标准普尔(Standard and Poor),从中减去了5个最大的价格峰值。这种飞跃无疑破坏了分析,在许多研究中,它被认为是(非分析性的)特例。 “不可思议的巧合,主的干预。好吧,有一件事,你可以把它放在一旁。”主对这张图的干预,事实证明,恰好有五种干预与其他一切一样重要。换句话说,主的干预不能搁置。
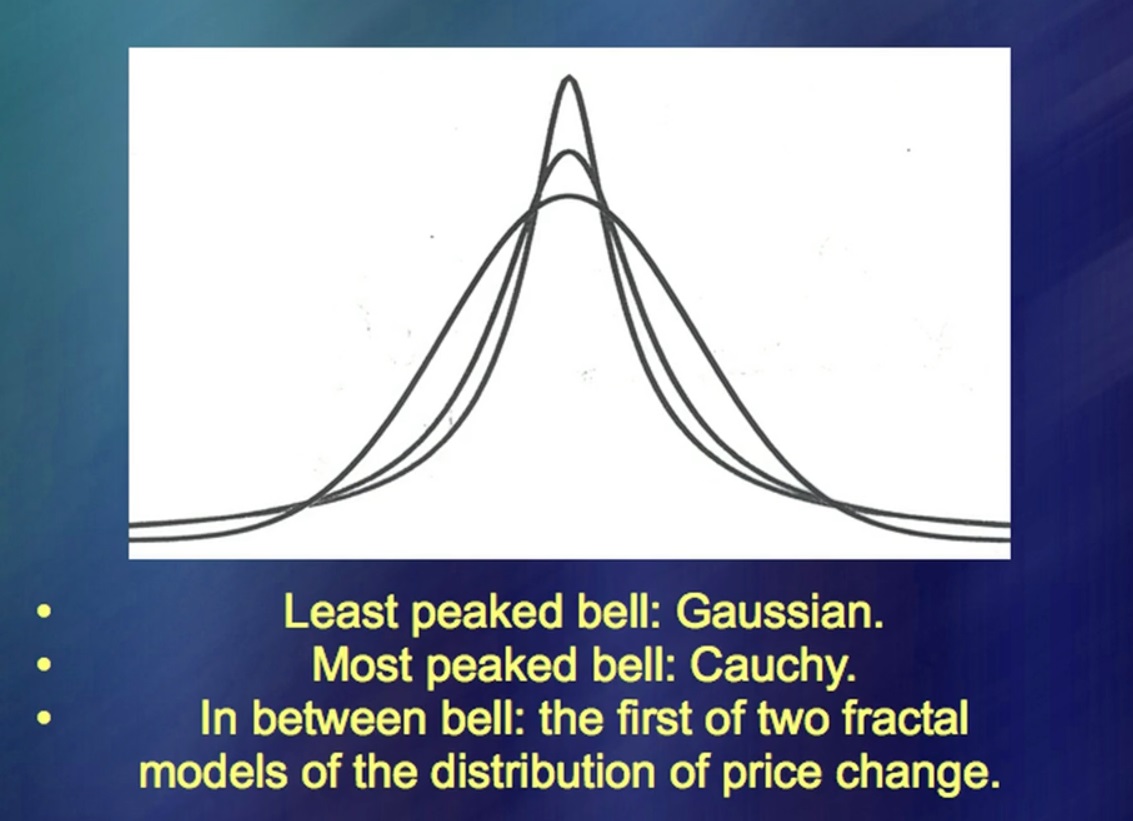
这是一个存在,它是分析的对象。如果您与他们打交道,您还可以应对价格变动。但是我还没有弄清楚这些跳跃,因此您可以根据需要尽可能多地分析所谓的噪声,但是这种分析是没有意义的。这些曲线显示了影响。

现在,我将转到最后一个主题-以我的名字命名的集合。从某种意义上讲,这就是我一生的故事。我的青春期在法国度过,那年被德国占领。因为我以为在任何时候我都可能不会,所以我有一个很大的梦想。战争结束后,我再次遇到了我的叔叔。我叔叔是一位杰出的数学家,他说:“这对您来说是个问题。 25年前,我无法解决它,而且没人能解决。这是由一位名叫加斯顿·朱莉亚(Gaston Julia)的数学家和另一名名叫Pierre Fatou的数学家的构建。如果您在这里能找到新的东西-任何东西-请考虑您的职业生涯得到了保障。”很简单。我开始研究这个问题,并且像成千上万尝试在我之前这样做的人一样,没有取得任何成就。
但是随后出现了计算机。而且我决定我不应该将计算能力应用于新的数学问题(例如,这种弯曲的东西:这是一个新问题),而不仅仅是旧问题。我从所谓的实数切换到从直线上的点到复数,这些都是平面上的点,也就是说,此问题中需要什么。结果就是这样一个数字。

这是非常复杂的。该方程式隐藏在其中:z转换为z ^ 2 + c。如此简单而无聊,那么无趣。现在让我们运行一次,两次...两次就足够了。关于奇迹!这就是出现的情况。我不会在这里解释这些事情,但是事实证明这就是事实。


如此一遍又一遍又一遍地获得如此复杂,和谐和美的图形。我的主要发现是这些岛屿的形状或多或少与整个形状相同。结果就是如此令人惊叹的巴洛克式珠宝。

所有这些简短的公式,其中包含所有内容-多少钱? -五个图标。这就是结果。

添加颜色的原因有两个。首先,由于数字是如此复杂,以至于很难理解数字的含义。您需要选择某种系统以将其反映在飞机上。因此,我将始终以不同颜色表示图形作为原则:一种颜色表示一种事物,另一种颜色表示另一种事物,依此类推。它是如此艰苦。
1990年,我在英国的剑桥大学获得了大学的奖项。三天后,一名飞行员飞越田野,看到了这一点。

这样的东西从哪里来?当然-来自外星人。
剑桥的一家报纸发表了一篇有关这一“发现”的文章,第二天,它收到了5,000封信,说这是曼德布罗特集,非常大。

让我完成。这幅图是通过纯数学获得的。如果不断重复,简单的规则就会创造无底的奇迹。
译者:Namik Kasumov,译者
:Ekaterina Tsvetkova。

通过参加SkillFactory的付费在线课程,了解如何从头开始或获得技能和薪资水平提高的详细信息:
- Machine Learning (12 )
- Data Science (12 )
- (9 )
- «Python -» (9 )