机器学习(ML)已经在改变世界。 Google使用IO来提供和显示对用户搜索的响应。 Netflix用它推荐晚上的电影。 Facebook使用它来建议您可能认识的新朋友。
机器学习从未像现在这样重要,同时又变得如此难以学习。这个领域充满了行话,并且不同的ML算法的数量每年都在增长。
本文将向您介绍机器学习的基本概念。更具体地说,我们将讨论当今9种最重要的ML算法的基本概念。
推荐系统
要从0开始构建完整的推荐系统,需要对线性代数有深入的了解。因此,如果您从未学习过该学科,则可能很难理解本节中的某些概念。
但请放心-scikit-learn Python库使构建CP非常容易。因此,您不需要具备线性代数的丰富知识即可构建有效的CP。
CP如何工作?
推荐系统主要有2种:
- 基于内容
- 协同过滤
基于内容的系统会根据您已经使用的元素的相似性提出建议。这些系统的行为与您期望CP行为完全相同。
协作式CP过滤基于关于用户如何与元素交互的知识(*注:与其他用户的行为与用户相似的元素的交互为基础)提供建议。换句话说,他们使用“人群的智慧”(因此在该方法的名称中为“协作”)。
在现实世界中,协作式CP过滤比基于内容的系统普遍得多。这主要是由于它们通常会产生更好的结果。一些专家还发现协作系统更易于理解。
CP协作过滤还具有基于内容的系统中没有的独特功能。即,他们具有自行学习功能的能力。
这意味着它们甚至可能开始根据您甚至没有提供该系统正常工作的特性或特征来定义元素中的相似性。
协作过滤有2个子类别:
- 基于模型
- 基于邻域
好消息是,您无需了解这两种协作式CP过滤之间的区别即可在ML中获得成功。只知道有几种类型就足够了。
总结
这是我们在本文中对推荐系统了解到的内容的快速回顾:
- 实际推荐系统示例
- 不同类型的推荐系统,以及为什么比基于内容的系统更频繁地使用协作过滤
- 推荐系统与线性代数的关系
线性回归
线性回归用于基于一组x值来预测y值。
线性回归的历史
线性回归(LR)由弗朗西斯·加尔顿(Francis Galton)于1800年发明。高尔顿是一位研究父母与孩子之间纽带的科学家。更具体地说,高尔顿研究了父亲的成长与儿子的成长之间的关系。高尔顿的第一个发现是事实,即儿子的成长通常与父亲的成长大致相同。这不足为奇。
后来,高尔顿发现了一些更有趣的东西。通常,儿子的成长更接近所有人的平均身高,而不是父亲的成长。
高尔顿称这种现象为回归。他特别指出:“儿子的身高倾向于下降(或向平均身高偏移)。”
这导致了统计学和机器学习的整个领域,称为回归。
线性回归数学
在创建回归模型的过程中,我们要做的就是在数据集中尽可能靠近每个点的位置绘制一条线。
这种方法的一个典型示例是“最小二乘”线性回归方法,该方法计算上下方向上的一条线的紧密度。
举例说明:
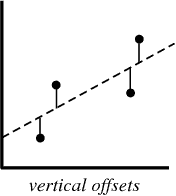
创建回归模型时,最终产品是一个方程式,您可以使用它来预测x值的y值,而无需事先知道y值。
逻辑回归
Logistic回归与线性回归相似,不同之处在于它不计算y的值,而是评估给定数据点属于哪个类别。
什么是逻辑回归?
Logistic回归是用于解决分类问题的机器学习模型。
以下是MO的分类任务的一些示例:
- 电子邮件垃圾邮件(垃圾邮件还是非垃圾邮件?)
- 汽车保险索赔(赔偿或维修?)
- 疾病诊断
这些任务中的每一个显然具有2类,使其成为二进制分类任务的示例。
Logistic回归对于二进制分类问题非常有效-我们只需将不同的类别分别分配给0和1。
为什么要进行逻辑回归?因为您不能将线性回归用于二进制分类预测。它根本不起作用,因为您将尝试通过具有两个可能值的数据集绘制一条直线。
此图可以帮助您理解线性回归为什么不利于二进制分类:
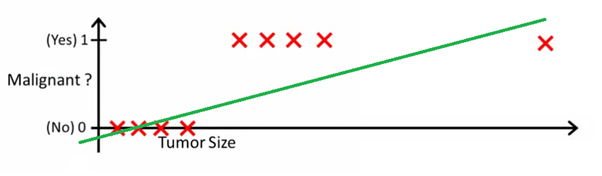
在此图像中,y轴表示肿瘤为恶性的可能性。1-y值表示肿瘤良性的可能性。如您所见,线性回归模型在预测数据集中大多数观测值的可能性方面表现非常差。
这就是逻辑回归模型有用的原因。它趋向最佳拟合线,这使其更适合预测定性(分类)数据。
这是一个在同一数据上比较线性和逻辑回归模型的示例:
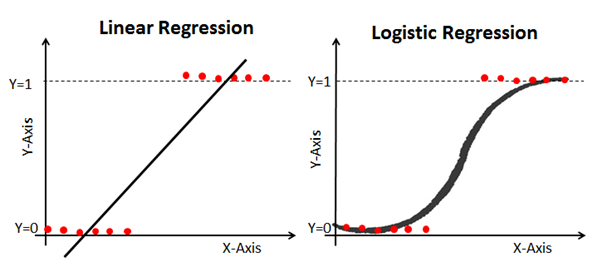
乙状结肠(乙状结肠功能)
逻辑回归之所以会扭结,是因为它没有使用线性方程式进行计算。相反,逻辑回归模型是使用S形构建的(也称为逻辑函数,因为它在逻辑回归中使用)。
您不必彻底记住乙状结肠即可成功获得ML。尽管如此,了解此功能还是有帮助的。
Sigmoid公式:Sigmoid的
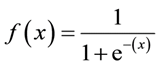
主要特征,值得处理-无论您将此函数传递给哪个值,它都将始终返回0-1范围内的值。
使用逻辑回归模型进行预测
为了使用逻辑回归进行预测,通常需要准确定义截止点。该临界点通常为0.5。
让我们使用上图中的癌症诊断示例在实践中了解此原理。如果逻辑回归模型返回的值小于0.5,则该数据点将被归类为良性。类似地,如果乙状结肠的值大于0.5,则肿瘤被分类为恶性。
使用误差矩阵衡量逻辑回归的有效性
误差矩阵可用作比较MO中的真实阳性,真实阴性,假阳性和假阴性分数的工具。
当用于测量逻辑回归模型的性能时,误差矩阵特别有用。这是一个如何使用误差矩阵的示例:
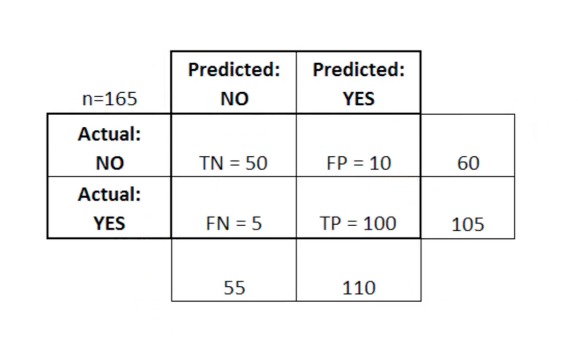
在此表中,TN代表真负,FN代表假负,FP代表假正,TP代表真正。
如果误差矩阵中存在``弱''象限,则误差矩阵可用于评估模型。例如,她的假阳性数可能异常高。
在某些情况下,确保模型在错误矩阵的特别危险区域中正确执行也非常有用。
例如,在这个癌症诊断示例中,您要确保模型没有太多误报,因为 这意味着您将某人的恶性肿瘤诊断为良性。
总结
在本节中,您第一次熟悉ML模型-Logistic回归。
这是您对逻辑回归学到的内容的快速摘要:
- 适用于逻辑回归的分类问题类型
- 逻辑函数(S型)始终提供介于0和1之间的值
- 如何使用临界点通过逻辑回归模型进行预测
- 为什么误差矩阵对衡量Logistic回归模型的性能有用
K最近邻居算法
当类别多于2个时,k最近邻算法可以帮助解决分类问题。
什么是k近邻算法?
这是基于简单原理的分类算法。实际上,该原理是如此简单,以至于最好以一个示例来演示它。
想象一下,您拥有足球运动员和篮球运动员的身高和体重数据。 k最近邻居算法可用于预测新玩家是足球运动员还是篮球运动员。为此,算法确定最接近研究对象的K个数据点。
此图通过参数K = 3展示了这一原理:
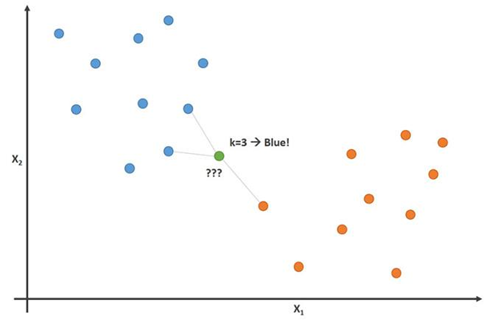
在此图像中,足球运动员是蓝色,篮球运动员是橙色。我们尝试分类的点是绿色。由于最接近绿点的大多数(3个中的2个)标记为蓝色(足球运动员),因此K近邻算法会预测新运动员也将是足球运动员。
如何建立K近邻算法
构建此算法的主要步骤:
- 收集所有数据
- 计算从新数据点x到数据集中所有其他点的欧几里得距离
- 按距离x的升序对数据集中的点进行排序
- 使用与大多数K最近数据相同的类别来预测答案x
K最近邻算法中K变量的重要性
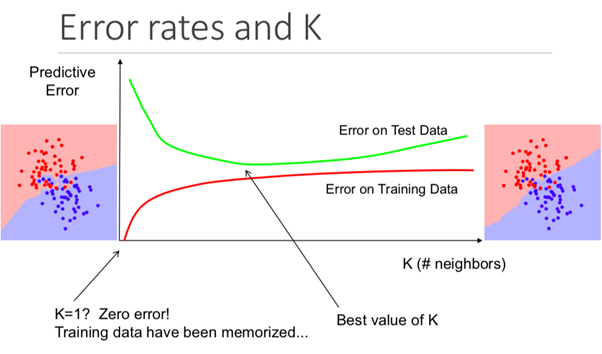
虽然从一开始可能并不明显,但在此算法中更改K值将更改新数据点所属的类别。
更具体地说,K值太低会导致您的模型在训练数据集上进行准确预测,但对测试数据却极为无效。另外,K太高会使模型不必要地复杂。
下图完美地展示了这种效果:
K最近邻算法的优缺点
总结一下我们对该算法的介绍,让我们简要讨论一下使用它的优缺点。
优点:
- 该算法简单易懂
- 对新训练数据进行简单模型训练
- 在分类任务中可使用任意数量的类别
- 轻松将更多数据添加到大量数据
- 该模型仅包含2个参数:K和您要使用的距离度量(通常是欧几里得距离)
缺点:
- 计算成本高,因为 您需要处理全部数据
- 不适用于分类参数
总结
关于您最近了解的K最近邻居算法的摘要:
- 该算法可以解决的分类问题(足球或篮球运动员)的示例
- 该算法如何使用到相邻点的欧几里得距离来预测新数据点属于哪个类别
- 为什么K值对预测很重要
- 使用K最近邻算法的优缺点
决策树和随机森林
决策树和随机森林是树方法的两个示例。更准确地说,决策树是ML模型,用于通过逐个循环遍历数据集中的每个函数进行预测。随机森林是决策树的集合(委员会),决策树使用数据集中对象的随机顺序。
什么是树法?
在深入研究ML中基于树的方法的理论基础之前,从示例开始是有帮助的。
假设您每个星期一都在打篮球。而且,您总是邀请同一个朋友来和您一起玩。有时朋友来了,有时却没有。是否做出决定取决于许多因素:哪种天气,温度,风和疲劳。您开始注意到这些功能,并随着朋友决定是否使用这些功能进行跟踪。
您可以使用此数据来预测您的朋友今天是否来。您可以使用的一种技术是决策树。外观如下:
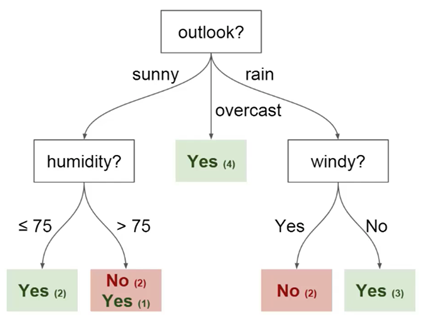
每个决策树都有两种类型的元素:
- 节点:根据某个参数的值拆分树的位置
- 边:导致下一个节点的分割结果
您可以看到该图具有外观,湿度和
刮风的节点。还有这些参数中每一个的每个潜在值的方面。
在开始之前,您还应该理解以下两个定义:
- 根-树分割开始的节点
- 叶子-预测最终结果的最终节点
您现在已经对什么是决策树有了基本的了解。在下一节中,我们将介绍如何从头开始构建这样的树。
如何从头开始构建决策树
建立决策树比听起来要难。这是因为确定将数据划分为哪些分枝(特征)(这是来自熵和数据获取的主题)在数学上具有挑战性。
为了解决这个问题,机器学习专家通常使用许多决策树,运用随机选择的特征集将树划分为决策树。换句话说,在每个单独的分区为每个单独的树选择新的随机特征集。这种技术称为随机森林。
通常,专家通常选择一组随机特征的大小(以m表示),以使其成为数据集中特征总数(以p表示)的平方根。简而言之,m是p的平方根,然后从m中随机选择一个特定的特征。
使用随机森林的好处
想象一下,您正在使用具有“强”特性的大量数据。换句话说,此数据集中的一个特征在最终结果方面比该数据集的其他特征更可预测。
如果您要手工构建决策树,则可以将此特性用于树中的“顶部”分区。这意味着您将拥有几棵与预测高度相关的树。
我们想要避免这种情况,因为 使用高度相关变量的平均值不会显着减小方差。通过为随机森林中的每棵树使用随机的特征集,我们对树进行解相关,从而减少了所得模型的方差。在使用随机森林而不是手工构建的决策树时,这种去相关是一个主要优势。
总结
因此,这是您刚刚从决策树和随机森林中学到的内容的快速摘要:
- 可以使用决策树预测其解决方案的问题的示例
- 决策树元素:节点,面,根和叶
- 如何使用一组随机特征使我们能够建立一个随机森林
- 为什么使用随机森林进行变量的去相关会有助于减少结果模型的方差
支持向量机
支持向量机是一种分类算法(尽管从技术上讲,它们也可以用于解决回归问题),该算法将一组数据按类别之间最大的“空白”划分为各个类别。当您查看以下示例时,此概念将变得更加清晰。
什么是支持向量机?
支持向量机(SVM)是一种监督的ML模型,具有用于分析数据和识别模式的适当学习算法。SVM可用于分类任务和回归分析。在本文中,我们将专门研究使用支持向量机来解决分类问题。
谅解备忘录如何运作?
让我们更深入地了解谅解备忘录的真正工作原理。
我们提供了一组训练示例,每个训练示例都被标记为属于2类之一,并且使用这组SVM建立了一个模型。该模型将新示例分为两类之一。这使SVM成为不可能的二进制线性分类器。
谅解备忘录使用几何按类别进行预测。更具体地说,支持向量机将数据点映射为空间中的点并将其分类,以使它们之间的距离尽可能宽。新数据点将属于特定类别的预测基于断点的哪一侧。
这是一个可视化示例,可帮助您理解MOU的直观含义:
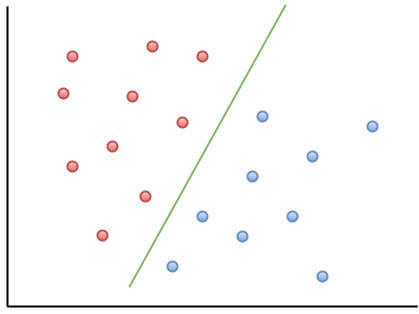
如您所见,如果新数据点落在绿线的左侧,则将其称为``红色'',如果在右侧,则将其称为``蓝色''。这条绿线称为超平面,是使用谅解备忘录的重要术语。
让我们看一下SVM的以下可视表示形式:
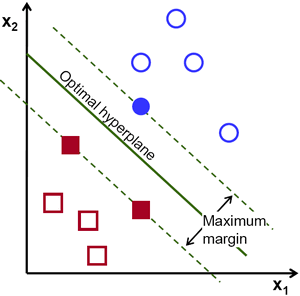
在此图中,超平面被标记为“最佳超平面”。支持向量机理论将最佳超平面定义为最大化不同类别的两个最近数据点之间的场的超平面。
如您所见,字段边界确实会影响3个数据点-红色类别中的2个数据点和蓝色类别中的1个数据点。这些与场的边界接触的点称为支持向量,因此称为名称。
总结
这是您刚刚了解到的关于支持向量机的简要快照:
- MOU是监督式ML算法的示例
- 支持向量可用于解决分类问题和进行回归分析。
- MOU如何使用超平面对数据进行分类,从而使数据集中各个类别之间的边距最大化
- 那些触及划分域边界的数据点称为支持向量。方法名称的来源。
K均值聚类
K-Means方法是一种无监督的机器学习算法。这意味着它接受未标记的数据,并尝试将数据中相似观察结果的群集聚类。K-Means方法对于解决实际应用非常有用。以下是适合此模型的一些任务的示例:
- 营销团队的客户细分
- 文件分类
- 为Amazon,UPS或FedEx等公司优化运输路线
- 识别并应对城市中的犯罪地点
- 专业运动分析
- 预测和预防网络犯罪
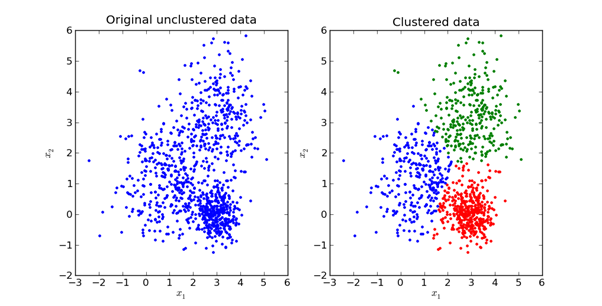
K-Means方法的主要目标是将数据集划分为不同的组,以使每个组内的元素彼此相似。
这是实际情况的直观表示:
在下一节中,我们将探讨K-Means方法背后的数学原理。
K-Means方法如何工作?
使用K均值方法的第一步是选择要将数据划分为的组数。此数量是K的值,反映在算法名称中。K均值方法中K值的选择非常重要。稍后我们将讨论如何选择正确的K值,
接下来,您必须在数据集中随机选择一个点并将其分配给随机簇。这将为您提供开始数据的位置,您可以在该位置运行下一个迭代,直到集群停止更改为止:
- 通过获取每个群集中点的平均向量来计算每个群集的质心(重心)
- 将每个数据点重新分配到质心最接近该点的群集
在K均值方法中选择适当的K值
严格来说,选择合适的K值非常困难。选择“最佳” K值没有“正确”的答案,机器学习专业人员经常使用的一种方法称为“肘部方法”。
要使用此方法,您要做的第一件事是计算平方误差之和-您的算法对一组K值的标准偏差.K均值方法中的标准偏差定义为集群中每个数据点之间距离的平方之和。和这个星团的重心。
作为此步骤的示例,您可以计算2、4、6、8和10的K值的标准偏差。接下来,您将要生成标准偏差和这些K值的图表。您会看到随着K值的增加,偏差减小。
这是有道理的:根据一组数据创建的类别越多,每个数据点越有可能接近该点的群集的中心。
话虽如此,弯头法的主要思想是选择K值,RMS将在该K值处显着减慢下降速度。这种急剧下降在图表上形成了“肘”。
例如,这是RMS与K的关系图,在这种情况下,弯头法建议使用约6的K值。
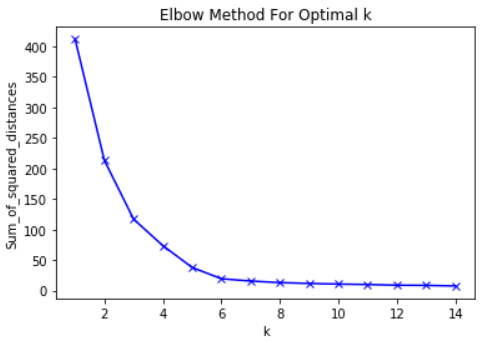
重要的是,K = 6只是对可接受K值的估计,K-Means方法中没有“最佳” K值。像ML中的许多东西一样,这是一个非常有情境的决定。
总结
这是您在本节中刚刚学到的内容的简要概述:
- 没有老师的ML任务示例可以通过K-means方法解决
- K-means方法的基本原理
- K-均值的工作原理
- 在该算法中如何使用弯头方法为K参数选择合适的值
主成分分析
主成分分析用于将具有多个参数的数据集转换为具有较少参数的新数据集,并且此数据集中的每个新参数都是先前存在的参数的线性组合。这种转换后的数据倾向于以更为简单的方式证明原始数据集的大部分方差。
什么是主成分法?
主成分分析(PCA)是一种ML技术,用于研究变量集之间的关系。换句话说,PCA检查变量集以确定这些变量的基本结构。PCA有时也称为因子分析。
基于此描述,您可能会认为PCA与线性回归非常相似。但这种情况并非如此。实际上,这两种技术有几个重要的区别。
线性回归和PCA之间的差异
线性回归确定整个数据集的最佳拟合线。主成分分析可识别数据集的多个正交最佳拟合线。
如果您不熟悉正交一词,则仅表示直线彼此成直角,如地图上的北,东,南和西。
让我们看一个示例,以帮助您更好地理解这一点。

看一下这张图中的轴标签。x轴的主要成分解释了此数据集中73%的方差。y轴的主要成分解释了数据集中约23%的方差。
这意味着仍有4%的方差无法解释。您可以通过在分析中添加更多主成分来减少此数量。
总结
您刚刚学到的有关主成分分析的摘要:
- PCA尝试找到确定数据集中变异性的正交因子
- 线性回归与PCA的区别
- 在数据集中渲染时正交主成分是什么样子
- 添加其他主要成分可以帮助更准确地解释数据集中的方差